Бурение грунтовых зондов, установка энергетических колодцев

Две системы точек S и S’ называются геометрически подобными, если между точками этих систем можно установить взаимно однознач­ное соответствие таким образом, что любые два соответственных отрезка, соединяющих две соответственные точки, находятся в одном и том же отношении Ch т. е.

А:Ак1АА’к = С,. (12.1)

Отсюда неизбежно следует равенство соответственных углов, а также пропорциональность соответственных площадей с коэффици­ентом пропорциональности С? и пропорциональность объемов с ко­эффициентом пропорциональности Cf.

В ряде источников даются и другие определения геометрического подобия. Например, в [5] это определение звучит так; два тела, имеющие различные размеры, подобны, если в результате равномер­ной деформации они полностью совпадают.

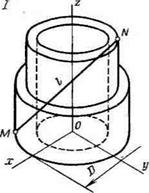
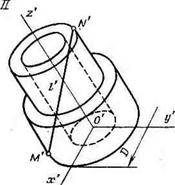
Рассмотрим два тела (короночных кольца): / и II (рис. 12.1). Поместим тело II (модель) в тело / (натура) так, чтобы их сходственные точки О и О’ совпадали. Затем тело / будем дефор — 220

мировать и вращать. Если в результате равномерной деформации тела / все точки контура (или границы обеих тел) совпадут, то эти тела подобны. Положение подобных тел, при котором в результате равномерной деформации одного из них, контуры совпадают, называ­ется сходственным ‘расположением. На рис. 12.1 показано несходст­венное положение тел. Чтобы получить сходственное положение, тело / или U необходимо вращать до тех пор, пока оси х, у и z станут параллельными осям У, у и У. В этом случае оси также станут сходственными.

В подобных телах для любой точки (в одном из них) может быть найдена сходственная точка в другом (например, М и М’, N и N’). Если через сходственные точки в телах I и II провести отрезки / и то при равномерной деформации они совпадут. Указанные отрезки называются сходственными линейными парамет­рами. Наружный или внутренний диаметр колец также будут сход­ственными параметрами.

Так как при равномерной деформации все размеры тела изменя­ются в одинаковое число раз, то для двух подобных тел должно соблюдаться следующее соотношение линейных параметров:

где хм, Ум, 7-м—координаты точки М (или любой другой точки) тела /; /—параметр тела /; хм-, Ум-, 7-м-—сходственные координаты точки М’; Г—сходственный параметр тела II; Q—множитель по­добия, показывающий во сколько раз нужно изменить размеры одного из подобных тел, чтобы оба тела совпали.

При моделирований ряда процессов удобно переходить к безраз­мерным зависимостям между параметрами, изучаемых объектов.

Например, все координаты и параметры тел / и // можно выразить 1 через один из сходственных параметров (допустим, наружный диаметр D и £>’ короночного кольца). Тогда для реального тела (натуры) и подобного тела (модели) получим ряд безразмерных величин:

хм v >:д< zm.. I,

-d-Xm’~d-Ym»d-Zm’d-l и т д-;

wr УМ у. .( /|Л

и •Д — (12.3)

п R %м xMD’

Легко обнаружить, что отношение —— =—————— =— = 1, и, следо-

Хм‘ Xm’D Ci>

вательно, все остальные отношения безразмерных координат и па­раметров подобных тел равны единице:

|м=^=|м = Т = 1 (124)

ЛМ‘ 1 М‘ ^М’ ^

откуда получим, что

Хм = ХМ’, Ym=YM’, ZM = ZM’, L = L’ и т. д. (12.5)

Таким образом, равенства (12.4) и (12.5) выражают весьма существенное свойство геометрически подобных систем: если в качестве масштабов для измерения длин выбрать два сходственных параметра тел, то безразмерные координаты сходственных точек, а также безразмерные другие сходственные параметры между собой соответ­ственно равны.

Комментарии запрещены.