Бурение грунтовых зондов, установка энергетических колодцев

В процессе производства геологоразведочных и изыскательских работ широко применяется вибрационное и ударно-вибрационное бурение скважин. Экспериментальные исследования показали, что при этом способе в канате и мачте возникают значительные динамические нагрузки, изменяющиеся в довольно широких пределах — от 1 ■ 104 190

до 3 ■ 105 H и более. Выясним природу этих усилий, пользуясь простейшим аппаратом прямолинейных колебаний точки.

Процесс вибробурения скважин можно расчленить на следующие составные операции примерно с одинаковым характером возникающих нагрузок: 1) собственно процесс вибропогружения зонда; 2) процесс подъема инструмента из скважины; 3) процесс извлечения прихвачен­ного на забое инструмента с использованием вибропогружателя; 4) процесс очистки зонда от породы также с применением вибро­погружателя.

Собственно процесс. вибропогружения зонда характеризуется не­значительными вертикальными нагрузками на канат и мачту. Процесс подъема инструмента также не приводит к появлению больших динамических нагрузок. Исключение составляет лишь случай, когда из стенки скважины происходит вываливание валуна и крупной гальки и снаряд мгновенно расклинивается в скважине. Но это уже будет случай прихвата, и он должен рассматриваться особо.

Опасным случаем нагружения каната и мачты является случай очистки зонда от породы с помощью вибропогружателя. Когда снаряд просто подвешен на канате при работающем вибропогружателе, этот случай особой опасности не представляет. Однако он становится чрезвычайно опасным, если мастер приподнимает снаряд, свободно сбрасывает его с включенным вибропогружателем и резко тормозит почти у поверхности земли. Этот прием иногда используется для выбивания из зонда керна, отобранного из плотных вязких глин. Вероятность обрыва каната в этом случае становится значительной.

Одно из наиболее опасных нагружений каната и мачты—извлече­ние лебедкой прихваченного на забое снаряда с включенным виб­ропогружателем. Именно при таком нагружении чаще разрываются ‘ канат и подвеска либо происходит деформация мачты.

С целью оценки возникающих динамических нагрузок в канате и мачте при работающем вибропогружателе рассмотрим два послед­них случая нагружения.

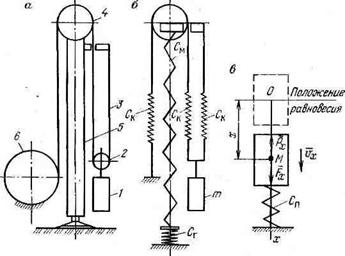
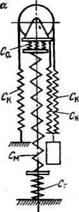
Расчетная схема для случая сбрасывания работающего вибропог­ружателя со снарядом и резкого его торможения при двухструнной талевой оснастке показана на рис. 9.1. Эта схема соответствует процессу вибробурения, осуществляемому вибробуровым агрегатом АВБ2М и некоторыми другими виброустановками. Предполагается, что канат, мачта и грунт, на который опирается мачта, обладают упругостью. Коэффициент жесткости одной ветви каната обозначим С(, коэффициент жесткости мачты См и коэффициент жесткости грунта Сг. На вибропогружатель действует восстанавливающая сила Спрх и вынуждающая сила Q = Q0sin col. Сопротивления колеба­ниям принимается равными нулю. Эти сопротивления в подавляющем большинстве случаев будут приводить к снижению нагрузок на канат и мачту. Таким дбразом, рассматриваемый процесс сведен к модели вынужденных колебаний материальной точки без сопротивлений [см. формулы (9.14) и (9.15)].

Рис. 9.1. Схема подвески вибропогружателя на мачте вибробурового агрегата при двухструнной талевой оснастке (я), эквивалентная ей динамическая модель (б), расчетная схема (в): / вибропогружатель; 2—талевый блок; 3 канат; 4 — блок; 5—мачта; 6 — лебедка

Определим постоянные интегрирования а и а. Будем считать, что л=0, х = Vo при t =0. Легко получить, что в этом случае а = 0, а амплитуда соответствует-

“=у-,Т^2 у — (9.24)

к А — со к

С учетом полученного результата выражение (9.15) запишется в виде

г:0 Р о. , , РО

71 I 7 р*ил»-г-у- к —О)" к) А —

г sin ю/. (9.25)

ог

Максимально возможное смещение вибропогружателя вниз про­изойдет в момент, когда совпадут фазы вынужденных и свободных колебаний системы и когда sin kr= 1 и sin ш = 1. В этом случае

v о, Л> /. «

Vimm-T-i-Tj 2 |_7 •- (926)

к к —со к,

Максимальное усилие в канате с учетом веса вибропогружателя определится по формуле

После подстановки

Г*° | р° (	1 “V
[ к А-2-со2	к).

Ршах—^ Р+:

Для системы, изображенной на рис. 9.1, б, приведенный коэф — . фициент жесткости

АС С С *-1 ‘-‘к

С ———- L4|> — If,

(9.29)

Пример. Пользуясь формулой (9.28), с учетом (9.29), подсчитаем мак­симальную нагрузку на канат и мачту вибробурового агрегата при следующих условиях: вибропогружатель сбрасывается с высоты 3 м и совершает свободное падение (г0 = 7,7 м ■ с1), на уровне земли он мгновенно останавливается, будучи включенным в работу. Максимальная вынуждающая сила вибропог­ружателя ВБ7 gmax=35 ООО Н, угловая скорость ш=132 с-1, вес вибропог­ружателя с буровым снарядом /’=5000 Н. Общий приведенный коэффициент жесткости системы (каната, мачты, грунта) изменяется в пределах Cnp = 10s — —28• 10s Н-м"1. При значении Cnp = 28-l0s Н м"1 усилия на канат и мачту будут максимальными. Так, на мачту в этом случае будет действовать динамическая нагрузка, достигающая 50-104 Н. Применительно к агрегату АВБ2М при См=14 107 Н^м"1, Сг = 5-106 Н-м"1, Ск = 3-106 Н-м"1, значение. С„р будет равно примерно 1,4-106 Н-м"1 и максимальное усилие на канат составит 11-104, а на мачту 33-104 Н (грузоподъемность мачты агрегата составляет 12 -104 Н). Очевидно, что для самоходных вибробуровых агрегатов типа АВБ2М такие нагрузки превышают допустимые й их следует по возможности уменьшать. Иными словами, производить очистку стакана от грунта описанным способом необходимо запрещать.

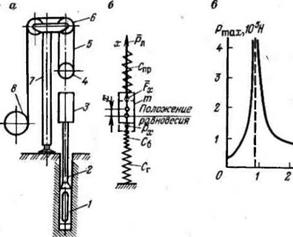
Рассмотрим случай извлечения прихваченного на забое снаряда с помощью статического усилия, развиваемого лебедкой вибробурового агрегата и включенного в работу вибропогружателя (рис. 9.2). На рисунке приняты следующие обозначения: Р„ — постоянное усилие, развиваемое лебедкой; Спр—приведенный коэффициент жесткости элементов системы (каната, мачты, грунта под опорами мачты); С6—коэффициент жесткости бурильных труб, Ст — коэффициент жест­кости грунта, удерживающего буровой снаряд; х—текущая координата.

Рассматриваемый случай в динамическом отношении мало чем. отличается от рассмотренного выше. Если пренебречь сопротивлениями колебаниям, то дифференциальное уравнение движения вибропогружателя будет аналогично выражению (9.14), а его решение—выражению (9.15).

Для представленной системы приведенный коэффициент жесткости всей системы

Cfi-C, cfi+CV

г = С ^пр. о vnp

(9.30)

Для нахождения постоянных интегрирования а и а можно принять, что х=0, vx = 0 при / = 0. При более точных расчетах можно задать небольшую начальную скорость (не более 0,3—0,5 м-с-1), которая сообщается вибропогружателю вверх в процессе натяжения каната лебедкой.

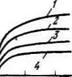
Рис. 9.2. К расчету динамических нагрузок, возникающих в канате и мачте в процессе извлечения прихваченного на забое инструмента с использованием вибропогружателя: , а—схема извлечения инструмента: /—виброзонд; 2—бурильные трубы; 3—вибропог­ружатель; 4—талевый блок; 5—канат; 6—кронблок; 7—мачта; 8—лебедка; б — мичсская расчетная модель; в—зависимость максимального усилия в канате Р ^ от приведенного коэффициента С о жесткости системы

■’лр. й

Используя начальные условия и рассуждая аналогично преды­дущему случаю, определим максимальное усилие в канате

toк „ т>-

(9.31)

-W _w,+

2 “ 2*2-<o2V

Сила тяжести вибропогружателя и бурового снаряда в данному случае входит в силу натяжения лебедки.

Поскольку глубина скважины меняется, а диапазон грунтов,! в которых производится бурение, достаточно широк, построим! зависимость Ртях=/(С„р.0) (рис. 9.2, в). Исходными данными для j построения графика следующие: РЛ = 6 104Н (за вычетом силы] тяжести), rmax= т • К)4 Н, w=132 с-1. График показывает, что при1] данной технологии извлечения в канате могут возникнуть очень большие нагрузки, а в резонансной зоне—вплоть до бесконечности. Однако при1- реальном извлечении снаряда всегда будут сопротивления, которые J исключают возможность появления бесконечных нагрузок. Однако при j этом величина максимальных нагрузок может быть значительной.

При глубине скважины 20 м и наружном диаметре бурильных труб. 0,0635 м с коэффициентом жесткости Сб=11 Ю6 Н-м-1, приняв Сг=5х х10б—107 Н-м-1 получим, что С„р.0=(4,84-^6,64) 106 Н-м-1. Система оказывается весьма близкой к резонансной зоне, и нагрузка на канат в этом случае будет составлять 7,5-105—10б Н, а на мачту (22,5-^30)105 Н, 194

-ft
•ft	ft
‘ft	ft

Л	1 2 3	1—1— 1
— :J
Li—— 1_		С——- 1_____ 1__ L.

№

2 4

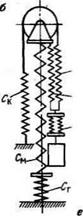
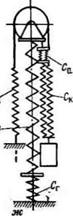
Рис. 9.3. Динамические схемы подвески вибропогружателя на мачте с амор­тизатором и графики зависимости приведенного коэффициента жесткости системы от коэффициента жесткости амортизатора: а—амортизатор на мачте; б—амортизатор над вибропогружателем; в —амортизатор на неподвижном конце каната; г—график приведенного коэффициента жесткости системы без амортизатора; д, е, ж—зависимость приведенного коэффициента жесткости системы от коэффициента жесткости амортизатора, установленного соответственно на мачте, над вибронотужатсзем и ни неподвижном конце каната; / — С ~ 8 ■ 10f’ Н м 1, 2— С =5 ■ 10 Н-м ‘3 — С =3-10‘ Н-м’1; 4—С =2-106 Н-м"1 ‘

2 ft,/(7H/H

г <

Снижение столь больших динамических нагрузок может быть достигнуто разлйчными путями. Радикальной мерой является установ­ка амортизаторов. Теоретической предпосылкой для использования •амортизаторов являются формулы (9.28) и (9.31). Из них следует, что уменьшая Спр.0, можно снизить и Ртак.

При двухступной талевой оснастке (а также при любой другой оснастке с неподвижным концом каната) принципиально возможны три схемы установки амортизаторов: на мачте, над вибропогружателем и на неподвижном конце каната (рис. 9.3).

Для первой схемы приведенный коэффициент жесткости системы С„р при заданном* коэффициенте жесткости амортизатора Ся определя­ется выражением

(9.32)

С’

___________ 4С, СмСгСа__________

‘ 3 С. См Сг+9 С. (СмО + С’м С„ + С, С„) •

для второй схемы

АС. С. С.С.

С" =- ‘—up.

СМСГ (4СЖ + ЗС„)+9СЯС. (Гм + Сг) ’ для третьей схемы ‘АС С С С

(9.34)

/-1» пр — ‘

СгСм(ЗСа + С,)+9С, Са(См + Сг)’

Для случая, близкого к практике, при длине ветви каната 6 м и диа — ]1 метре 15,5 мм, высоте мачты 7 м, наружном и внутреннем диаметре тру­бы мачты 0,168 м и 0,148 м имеет Са=3- 10б Н-м-1. См=14-107 Н-м-1.

На рис. 9.3, г, д, е, ж изображены зависимости приведенного коэффициента жесткости системы Спр от коэффициента жесткости j амортизатора Са для различных схем его установки при. различных Ст и Са = 5-105ч-5 106 Н-м’1.

Из представленных графиков видно, что предпочтительной яв­ляется установка амортизаторов на мачте (см. рис. 9.3, а, д). В этом случае амортизатор неподвижен, и, кроме того, при одном и том же коэффициенте жесткости амортизатора приведенный коэффициент жесткости системы будет меньше, чем для других схем его установки.

Для коэффициента жесткости грунта Сг = 5 106 Н м-1 приведен­ный коэффициент жесткости системы без амортизатора будет со­ставлять 14 — 10s. В этом случае в канате возникнет максимальная динамическая нагрузка, равная примерно 12-104 Н. Для той же жесткости грунта при установке на мачте амортизатора с C. d — = 2 106Н-м-1 приведенный коэффициент жесткости будет равен | примерно 543 ■ 103 Н ■ м — *, а максимальная динамическая нагрузка снизится до 7 ■ 104 Н. При постановке такого же амортизатора над вибропогружате­лем Дтах = 87 ■ 103 Н, на закрепленном конце каната Ртях= 107 ■ 103 Н.

Следует подчеркнуть, что амортизаторы можно устанавливать с любым минимально возможным коэффициентом жесткости. По­скольку рассматриваемая система совершает колебания в дорезонанс­ной зоне, уменьшение Спр смешает значение амплитуды на амп­литудно-частотной характеристике еще больше от резонансной зоны.

Комментарии запрещены.