Бурение грунтовых зондов, установка энергетических колодцев

В процессе бурения геологоразведочных скважин различными способами нередко возникает необходимость в отведении подвеше» ного на канате бурового инструмента, желонки, бурильной или обсадной трубы от устья скважины. Обычно такое отведение осущест­вляется с помощью специального крюка помощником бурильщика или рабочим. При этом тянуть он может не только с разным усилием, но под разным у^лом к вертикали. Требуется определить, на какую максимальную величину помощник бурильщика может оттянуть и удержать в этом положении подвешенное тело, а также под каким углом к вертикали целесообразно тянуть, чтобы при 76

заданном усилии удержать тело на максимальном расстоянии от устья. Большого практического значения задача не имеет. Однако представляет определенный методологический интерес.

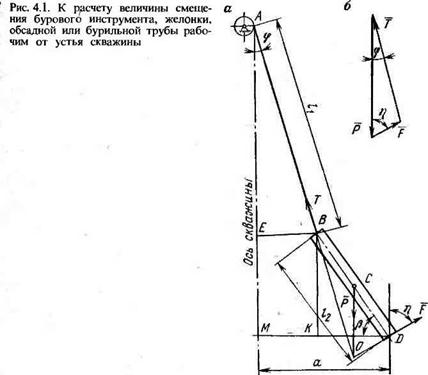
Расчетная схема задачи представлена на рис. 4.1, а. Тело (труба, желонка, инструмент) BD с силой тяжести Р, приложенной в центре тяжести тела (точке С), подвешено на канате АВ к блоку буровой мачты и оттягивается за конец желонки силой F в сторону помощником бурильщика. Требуется определить величину а. В задаче приходится вводить упрощающие допущения. Одно из них состоит в том, что сила тяжести считается приложенной посередине тела (ВС—CD), хотя точка приложения этой силы может быть несколько смещена и т. д.

Для наглядности задачу решим для определенных, близких к реальным, числовых значений параметров: Р=2000Н, АВ=11 =5 м, ВС=12 = Зм и /■= 150 Н.

Выбрав в качестве объекта равновесия тело и показав все действующие на него силы (активные Р и F) и реакцию связи (каната) Т, убеждаемся, что таких сил три, и, следовательно, линии их действия должны пересекаться в одной точке О. Выполнив соответствующие построения, в том числе силового треугольника

(рис. 4.1, б), легко убедиться, что искомый отрезок а может быть представлен как сумма двух отрезков:

a=MK+KD. (4.1)

Но MK=BE=llsinq>, a KD = l2 cosp. Задача, таким образом, сводится к отысканию углов ср и Р:

a=/i sincp-f /2cosp. (4.2)

Соответствующие тригонометрические функции углов ф_и Р будем отыскивать в функции угла т) (угла приложения силы F).

На основании рассмотрения силового треугольника (см. рис. 4.1, б) по теореме синусов можно записать

TOC o "1-5" h z 17 ПГ П

(4.3)

sincp sinr) sin(l80—ф —г))’ откуда

T=Fsinr/sm<p, (4.4)

tgф = Fsinr|/(F—Fcosri). (4.5)

Но в формулу (4.2) входит БШф, а не 1§ф. Преобразуем 1§ф в sin ф:

sn^=Fsinr|/(F—Fcosr|)1/2. (4.6)

Для отыскания cosp воспользуемся уравнением статики

5>в(й)=о,

раскрывая которое, получаем

—Pl2 cos р/2+Fcos ц • /2 cos Р+Fsin г) ■ /2 sin Р = 0, (4.7)

откуда

tgP=(F—2Fcosri)/2Fsinri. (4.8)

Преобразуем тангенс угла в косинус

cos р=2Fsin 1) / (Р 2—4FFcos г|+4F2)1/2. (4.9)

Подставляя (4.6) и (4.9) в (4.2), получим

/iFsinr) . /22Fsinr)

° (F2-2FFcosTi + F2),/2’r(F2-4FFcosr1-|-4F2),/2′ 1 J

Если г) = 90° (тело оттягивается горизонтально), то

h F. hlF /J1t4

Я (F2 + F2)1/2^(F 2 + 4F2)1/2 l J

После подстановки численных значений входящих в формулу

(4.11) величин получим а «0,82 м.

78

Для нахождения атт возьмем частную производную от выражения (4.10) по г) и приравняем ее к нулю. Опуская промежуточные ‘ выкладки, получим следующее выражение:

U [(F 2 — 2FFcos r| + F2) cos г) — FFstn 2 r|]

(Р2 —2PFcosr| 4-F2)3/2 =

(4.12)

/2 [{Р2 —4PFcos г) +4F2) 2cos r| —4PFsin2 г|]

(Р 2—4PFcos Г| +4F2)3/2

i Вьщелить cost) в явном виде из выражения (4.12) затруднительно.

Задача может быть решена с помощью ЭВМ либо обычным : графическим построением (т. е. приближенно). Суть построения сво-

: дится к тому, что находят значение функции левой части выражения

; (4.12) и изображают в виде графика, на котором по оси абсцисс

| откладывается угол г|. Такой же график строится для правой части

■ функции выражения (4.12); абсцисса точки пересечения двух графиков и дает искомое значение угла. В нашем случае г|«83° и атах = 0,84 м.

Из приведенного следует, что лучше всего оттягивать тело от скважины под небольшим углом к горизонту (вверх).

■ Представленная задача имеет ряд особенностей. Заметим, что : такие несложные статические задачи вызывают у студентов при

решении определенные трудности, которые связаны с нетривиаль — . ностью самой задачи. Первая особенность состоит в том, что

в задаче сразу задают две силы (по модулю и направлению), а в качестве неизвестной величины выступает модуль третьей силы и, казалось бы, не имеющая отношения к задаче величина а. Может возникнуть вопрос—в задачах статики для системы сходящихся сил обычно требуется найти две неизвестные величины [в соответствии с уравнением равновесия (3.12)]. В данной задаче неизвестных величин действительно две, но силовой треугольник разрешается одним геометрическим действием. Вторая особенность состоит в необ­ходимости определить величину а. Вен тонкость задачи как раз ‘ и состоит в том, что при равновесии тела под действием приложенных

сил их направления должны пересечься в одной точке. Отсюда L отрезок KD строго определяется положением тела, т. е. углом р,

что является следствием условия равновесия.

Наконец, третья особенность задачи состоит в том, что отыскание угла, при котором тело может быть оттянуто на максимальную I величину, требует ее решения как оптимизационной. Подобного рода

задачи нередки в практике разведочного бурения.

Комментарии запрещены.