ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СПУСКАЕМОГО В СКВАЖИНУ СНАРЯДА
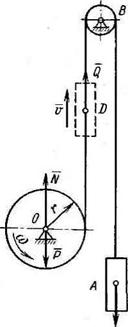
На расторможенный барабан лебедки радиусом г весом Р намотан канат, к концу которого подвешен буровой снаряд А весом Q (рис. 7.3). Пренебрегая массой каната, трением об оси и моментом инерции блока В определить ускорение движения снаряда, а также угловое ускорение барабана.
Данная задача во многих отношениях является характерной. Постановка задачи показывает, как следует упрощать сложную реальную механическую систему для выяснения ее основных наиболее существенных черт. В частности, в данной задаче не было учтено, что лебедка не является сплошным однородным цилиндром, сопротивления вращения лебедки не равны нулю, при сматывании каната момент инерции лебедки уменьшается, канат обладает массой, блок также обладает массой и сопротивления при его вращении также не равны нулю, при движении снаряда в скважине возникают сопротивления, сила тяжести спускаемого снаряда увеличивается за счет сматывающегося каната и т. д. Может возникнуть естественный вопрос, отражает ли в таком случае полученное решение задачи реальный процесс опускания снаряда? В итоге ответ на этот вопрос 158
Рис. 7.3. Схема снаряда, подвешенного на канате, намотанном на барабан лебедки
|
|
может дать только опыт. Но уже основываясь на полученном решении, можно утверждать, что реальные ускорения вряд ли будут существенно отличаться от теоретически вычисленных на основе приведенной расчетной схемы. Это объясняется тем, что влияние всех перечисленных факторов на процесс движения снаряда по сравнению с учитываемыми в задаче несущественно. В случае необходимости точного учета других факторов должны ставиться и решаться другие задачи.
В представленной на рис. 7.3 механической системе перемещаются два тела, одно из которых совершает поступательное (снаряд), другое — вращательное движение (барабан лебедки). Для решения задачи может быть использована теорема моментов — равенство (6.52) —относительно оси л, совпадающей с осью вращения лебедки.
Движущая система состоит из двух тел, поэтому ее кинетический момент
К^-к^+К^, (7.11)
где Абар, Асн — кинетический момент соответственно барабана и снаряда относительно оси г (снаряд мысленно переносим в точку D и считаем, что он движется вверх под действием направленной в ту же сторону силы Q).
Скорость снаряда v — олг, где со—мгновенная угловая скорость барабана.
|
Qv Qr2o K,„ — — r=—— |
|
(7.13) |
g g
После подстановки (7.12) и (7.13) в (7.11) получаем
|
|
(7.14)
Система приводится в движение только одной активной силой
|
Но da/dt — e. Тогда |
Q. Ее момент равен Qr. Подставляя полученные значения кинетического момента и момента силы в (6.52), имеем
(7.15)
|
(7.16) |
г 26 r{P+2Q)c’
и
|
|
|
W—£r — |
(7.17)
Предположим 6=2000 Н, Р=500Н, г=0,12 м, g=9,81 м с % тогда w = 8,72m-c-2, е = 72,67 с~2.