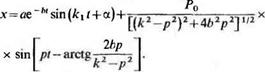Бурение грунтовых зондов, установка энергетических колодцев

В настоящей главе даются основные, принципиальные сведения, относящиеся к линейным (свободным и вынужденным) колебаниям материальной точки. Владение аппаратом линейных колебаний для инженера по разведочному бурению настоятельно необходимо. С од­ной стороны, этот аппарат вполне пригоден для решения конкретных задач из области бурения, с другой — без владения этим аппаратом ревозможно разобраться в более сложных колебательных явлениях и процессах. Следует также подчеркнуть, что на начальных этапах изучения любого колебательного явления в бурении необходимо стремиться к описанию его одной из наиболее простых расчетных схем с последующим усложнением этой схемы, если в том возникает потребность.

Изложение основ прямолинейных колебаний материальной точки начнем с рассмотрения свободных колебаний точки без учета силы сопротивления под действием только одной восстанавливающей силы F„, определяемой’выражением Fx——Cx, где С—коэффициент жест­кости; х— текущая координата колеблющейся точки.

Дифференциальные уравнения таких колебаний имеют вид

В выражении (9.1) к носит название угловой частоты свободных | колебаний:

(9.2)1 (9-3) ^

к1 — С/т,

где т — масса колеблющейся точки.

Общее решение уравнения (9.1) имеет вид

х =Ct sin kt + C2 cos kt,

где Ci и C2 — постоянные интегрирования.

Если вместо постоянных С) и С2 ввести постоянные в и а, но] такие, чтобы С^—а cos a, a С2 = а sin а, то легко можно получить второй вид решения дифференциального уравнения (8.1)

(9-4);

x=flsin(&f+a).

Колебания, совершаемые по закону (9.4), называются гармо — 1 ническими.

Величина а, равная наибольшему отклонению точки М от центра колебаний (положения статического равновесия), называется амп­литудой колебаний. Величина kt + a называется фазой колебаний, а a— начальной фазой. Промежуток времени, в течение которого точка I совершает одно полное колебание, называется периодом колебаний

(9.5)

Т = 2п/к.

(9.6) i

Значения Cj и С2 или а и а определяются по начальным условиям: х=х0, vx = v0 при ( = 0. Тогда

а={х1 + сЦк2)т, a=arctg(&xo/r0).

Постоянная сила Рх, приложенная к колеблющейся точке (или j телу), не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы Fx, а только смещает центр этих колебаний в сторону действия силы Рх на величину статического отклонения 6„ = РХ/С.

Аппарат свободных колебаний точки без сопротивления можно применять для изучения колебаний подвешенного на канате бурового инструмента.

Для свободных колебаний точки при наличии сопротивления, пропорционального скорости, дифференциальное уравнение будет следующим:

‘■^■+2Ь~+к2х=0, (9.7) 1

dr dl и

где b = р/2ш—коэффициент, имеющий размерность, с-.1; р—коэф­фициент сопротивления колебаниям.

Решение дифференциального уравнения (9.7) зависит от соотноше­ния величин Ь и к. Можно выделить три случая: 1) к>Ь; 2) к<Ь и 3) к=^Ь.

Рассмотрим первый случай. Он характерен для колебаний точкг Lc малым сопротивлением. Если ввести обозначение к1=(к2 — Ь2)112 то общее решение дифференциального уравнения (9.7) для этогс случая будет иметь вид

(9.8 (9.9

х = е~ы(С1 sin&i f+C2Coski t), или по аналогии с равенством (9.4) х = ае ~т sin [к t + а).

Входящие в выражения (9.8) и (9.9) величины Ct и С2, а такж а и а являются постоянными интегрирования и определяются п> начальным условиям.

Колебания, происходящие по закону (9.8) или (9.9), называю затухающими, так как благодаря множителю е~ы величина ае~ с течением времени убывает, стремясь к нулю.

Период затухающих колебаний определяется по формуле

(9. К

Тх=2п1(кг-Ь2У12.

Период затухающих колебаний всегда больше периода соответ ствующих гармонических колебаний.

Для случая, когда Ь>к, решение уравнения (8.7) имеет вид

(9.11.

…………………….. + С2е’-‘-г|’

где г—(Ь2—к2)112.

Наконец, для случая, когда Ь — к, решение будет следующим:

(9.12)

x=e-bt(Cit + C2).

Движение точки, описываемое выражениями (9.11) и (9.12), не будет колебательным, и она под действием восстанавливающей силы будет постепенно приближаться к положению равновесия (v = 0). Эти два случая относятся к движению точки в очень вязкой жидкости.

Рассмотрим теперь важный для практики случай колебаний, возникающих, когда на точку, кроме восстанавливающей силы Fx, действует периодически изменяющаяся со временем сила

(9.13)

Qx = Qo sin pt,

где Со—амплитудное значение силы; р—угловая частота изменения силы.

Сила Qx носит название вынуждающей, или возмущающей силы. Дифференциальное уравнение вынуждающих колебаний точки при отсутствии сопротивления записывается в виде

d2x, .

—f+k2x=P0sinpt, dt2

(9.14)

(9.15)

(9.17)

(9.18)

Первое слагаемое правой части уравнения (9.15) соответствует свободным колебаниям точки, второе—вынужденным. При р<к фазы вынужденных колебаний и вынуждающей силы все время совпадают. При р>к сдвиг фазами вынужденных колебаний и вынуждающей силы равен п (когда сила Qx имеет максимальное значение и направлена в одну сторону, колеблющаяся точка мак­симально смещена в противоположную сторону). В случае, когда р = к, т. е, когда частота вынуждающей силы равна частоте собственных колебаний, отмечается так называемое явление резонанса. При резонансе решение уравнения (9.14) имеет вид Р t x = asm(kt + a)—-^—cospt. (9.16) Как видно из (9.16), размахи вынужденных колебаний при резонансе возрастают пропорционально времени. Сдвиг фаз при резонансе всегда соответствует я/2. В заключение рассмотрим движение точки, на которую действуют восстанавливающая сила, сила сопротивления, пропорциональная скорости, и вынужденная сила. Дифференциальное уравнение колеба­ний точки для этого случая имеет вид

cl2x (1х. , .

—-, +k х= PoSinpt. At* At

Его общее решение запишется

dt2 dt

Рассматриваемые колебания также являются сложными. Они складываются из собственных (первое слагаемое правой части) и вынужденных (второе слагаемое). Собственные колебания благодаря сопротивлению довольно быстро затухают и по истечении некоторого промежутка времени <у, называемого временем установления, ими практически можно пренебречь. В технике нередко используют так называемый коэффициент динамичности

Кп А]Ъ$ >

(9.19) шплитуда вынужденных колебаний;

■ и> су г, ■ i J

80 = Оо/С; С—коэффициент жесткости. 188

Вынужденные колебания обладают следующими важными для практики свойствами:

1) амплитуда вынужденных колебаний не зависит от начальных условий;

2) вынужденные колебания при наличии сопротивлений не затухают;

3) частота вынужденных колебаний равна частоте вынуждающей силы и за исключением особых случаев не зависит от характеристик колеблющейся системы;

4) при малой вынуждающей силе можно увеличить амплитуду вынужденных колебаний, если уменьшить сопротивления, а частоту собственных колебаний системы сделать близкой частоте вынуж­дающей силы; обычно таким образом достигают усиления интен­сивности различных процессов (например, при вибропогружении различных элементов в грунты, при приготовлении глинистых рас­творов, разглинизации стенок скважины и т. д.);

5) при больших значениях вынуждающей силы можно существенно снизить амплитуду вынужденных колебаний (почти до нуля), если выбрать значение к много меньше р и увеличить сопротивления; это — один из эффективнейших методов борьбы с вибрацией в бурении. Обычно он осуществляется с помощью установки амортизаторов, коэффициент жесткости которых выбирается в соответствии с рас­четом. Смазка бурильных труб, а также применение специальных промывочных жидкостей существенно снижает вибрацию вращающей­ся колонны бурильных труб.

Вынужденные колебания, возникающие в различных элементах буровых устройств, как правило, являются следствием вращения несбалансированных масс. В одних случаях несбалансированность вредна и ее устраняют всеми возможными способами, в других — создают искусственно (например, в центробежных вибровозбудителях).

Все изложенное выше в полной мере может быть отнесено к крутильным колебаниям тел. Структура всех формул для крутильных колебаний тел будет аналогичной представленным выше. Однако в качестве координаты в этом случае будет угол поворота, в качестве массы точки — осевой момент инерции тела, в качестве сил — моменты сил и т. д.

Комментарии запрещены.