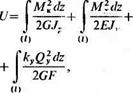Бурение грунтовых зондов, установка энергетических колодцев

При решении различных практических задач возникает необходи­мость определения перемещений, когда имеет место общий случай нагружения, а в поперечных сечениях возникают нормальные и попе­речные силы, изгибающие и крутящие моменты одновременно, к тому же брус может быть не только прямым, но может иметь малую кривизну или состоять из прямых участков, образующих плоскую или пространственную систему. Перемещения в этом случае наиболее просто находятся при помощи энергетических соотношений на основе общего выражения потенциальной энергии нагруженного бруса.

Определению потенциальной энергии предшествует анализ внут­ренних силовых факторов, возникающих в брусе. Этот анализ производится с помощью метода сечений и завершается построением эпюр изгибающих и крутящих моментов, а в тех случаях, когда это необходимо,— построением эпюр нормальных и поперечных сил. 246

Потенциальная энергия всего бруса определяется с помощью выражения

Г M)dz CN2c1z Г kxQldz

J 2EJy ’ J 2EF ’ J IGF

(О (о

где kx и к у—безразмерные величины, зависящие от геометрической формы сечения (для прямоугольного сечения бруса кх = ку = 6/5, для сплошного круглого сечения к= 10/9, для тонкостенного кругового профиля к — 2 и т. д.).

Если конструкция сложная и состоит из нескольких элементов, имеющих форму бруса, то после интегрирования в пределах каждого бруса должна быть суммирована энергия по числу составляющих элементов.

При определении перемещений в сопротивлении материалов пользуются теоремой Кастилиано, интегралом Мора и способом Верещагина. Подробно указанные способы рассмотрены в соответ­ствующей литературе, например в [8, 27]. Для этих же целей может быть использована и общая теорема взаимности работ и перемещений.

Комментарии запрещены.