ПОНЯТИЕ ОБ УСТОЙЧИВОСта РАВНОВЕСИЯ ДЕФОРМИРУЕМЫХ СИСТЕМ
ПОНЯТИЕ ОБ УСТОЙЧИВОСта РАВНОВЕСИЯ ДЕФОРМИРУЕМЫХ СИСТЕМ
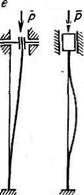
Под устойчивостью понимается свойство системы сохранять свое состояние при внешних воздействиях, а под потерей устойчивости— отклонение от исходного равновесного состояния системы. Для анализа устойчивости может быть выбрана, например, следующая идеальная схема. Однородный стержень имеет строго прямолинейную ось, его материал однороден, силы приложены по центру стержня. Этому стержню сообщается отклонение от положения равновесия. При этом рассматриваются отклонения, которые не только малы, но могут быть меньше любой малой, наперед заданной величины. Если после устранения причин, вызвавших отклонение, стержень возвращается в исходное состояние равновесия, то последнее считается устойчивым, если не возвращается—неустойчивым. Этот подход позволяет определить такие значения внешних сил, при которых устойчивое положение равновесия становится неустойчивым. Такие силы называются критическими и рассматриваются как предельные.
При расчете на устойчивость рабочая нагрузка назначается как п-я доля критической. Под величиной п понимается коэффициент запаса устойчивости, величина которого назначается в зависимости от конкретных условий.
В пределах малых перемещений для стержня, шарнирно закрепленного по концам, изгиб при потере устойчивости происходит по полуволне синусоиды и критическая сила
|
д |
|
ж |
|
|
|
|
|
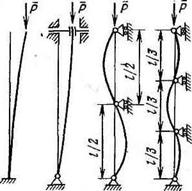
Рис. 13.3. Различные случаи закрепления концов стержня при продольном изгибе и значения коэффициента р: а—ц=1; о—ц=2: в — ц=2; г—ц=0,5; д—ц=1/3; е—ц=0,5; ж—ц=0,5; ? ц=0,7 |
|
б |
|
г |
|
|
Используя особенности упругой линии, полученное решение можно распространить и на другие случаи закрепления концов стержня. Обобщая все такие случаи, можно написать общее выражение для критической силы сжатого стержня (формулу Эйлера) в виде
P^n’EJHulV, (13.53)
где р—коэффициент приведения длины.
На рис. 13.3 показано несколько видов закрепления стержня и указаны соответствующие значения коэффициента приведения длины р. При учете пластических деформаций расчет стержня на устойчивость может быть заменен обычным расчетом по пределу текучести, но со сниженным допускаемым напряжением
ст. Р=*фотс, (13.54)
где ф — коэффициент снижения допускаемого напряжения.
Формула для расчета стержня на устойчивость выбирается в зависимости от так называемой гибкости
Х=р///, (13.55)
где i—радиус инерции сечения стержня.
Если ^>(л2£/пп)1/2, то пользуются формулой Эйлера, если Х<(п2Eju^Y12 — формулой (13.54). В указанных двух неравенствах стп — предел пропорциональности.
Значения коэффициента ф для различных материалов и при различных величинах гибкости приведены в табл. 13.2.
Для других различных случаев потери устойчивости существуют и применяются соответствующие методики расчета.
|
X |
Ст2, СтЗ, Сг4 |
Ст5 |
Чугун |
Дерево |
|
0 |
1 |
1 |
1 |
1 |
|
10 |
0,99 |
0,98 |
0,97 |
0,99 |
|
20 |
0,96 |
0,95 |
0,91 |
0,97 |
|
30 |
0,94 |
0,92 |
0,81 |
0,93 |
|
40 |
0,92 |
0,89 |
0,69 |
0,87 |
|
50 |
0,89 |
0,86 |
0,57 |
0,8 |
|
60 |
0,86 |
0,82 |
0,44 |
0,71 |
|
70 |
0,81 |
0,76 |
0,34 |
0,6 |
|
80 |
0.75 |
0,7 |
0,26 |
0,48 |
|
90 |
0,69 |
0,62 |
0,1 |
0,38 |
|
100 |
0,6 |
0,51 |
0,06 |
0,31 |
|
110 |
0,52 |
0,43 |
— |
0,25 |
|
120 |
0,45 |
0,36 |
— |
0,22 |
|
130 |
0,40 |
0,33 |
— |
0,18 |
|
140 |
0,36 |
0,29 |
— |
0,16 |
|
150 |
0,32 |
0,26 |
— |
0,14 |
|
160 |
0,29 |
0,24 |
— |
0,12 |
|
170 |
0,26 |
0,21 |
— |
0,11 |
|
180 |
0,23 |
0,19 |
0,10 |
|
|
190 |
0,21 |
0,17 |
— |
0,09 |
|
200 |
0,19 |
0,16 |
— |
0,08 |