Бурение грунтовых зондов, установка энергетических колодцев

Движение точки или твердого тела обычно рассматривается по отношению к неподвижной системе отсчета. Однако в ряде случаев возникает необходимость изучать движение точек и тел по отношению к системам отсчета, которые сами каким-то образом перемещаются по отношению к неподвижной системе. Определение кинематических характеристик точки в этом случае позволяет осуществлять анали­тический аппарат сложного движения точки.

Приведем ряд определений. Движение точки М относительно подвижной системы отсчета называется относительным. Движение подвижной системы отсчета относительно неподвижной называется переносньш. Движение точки М относительно неподвижной системы в этом случае будет называться абсолютным. Абсолютное движение складывается из относительного и переносного. Например, лодка перемещается по реке. Движение лодки по отношению к воде будет относительным, движение воды по отношению к берегам реки будет переносным, а движение лодки, каким его будет видеть наблюдатель, стоящий на берегу реки, будет абсолютным.

Задача кинематики в случае сложного движения точки состоит в том, чтобы зная относительное движение точки и переносное движение тела или пространства (подвижной системы отсчета), найти абсолютное движение точки, т. е. определить ее траекторию, скорость и ускорение в этом движении.

Абсолютной скоростью v и абсолютным ускорением w точки называют ее скорость и ускорение в абсолютном движении. От­носительной скоростыр аоти и относительным ускорением vvOTH точки называют ее скорость и ускорение в относительном движении, т. е. в ее движении по отношению к подвижной системе отсчета. Переносной скоростью йпер и переносным ускорением й’пср точки М называются скорость и ускорение той точки, неизменно связанной с пространством подвижной системы отсчета, с которой в данный момент совпадает движущаяся точка М.

Абсолютная скорость точки равна геометрической сумме перенос­ной и относительной, скоростей этой точки:

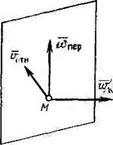
Рису 5.7. К определению направления вектора ускоре­ния ‘Кориолиса

Ускорение точки в сложном движении представляет собой геомет­рическую сумму трех ускорений: переносного, характеризующего изменение вектора переносной скорости точки в переносном движении; относительного, характеризующего изменение вектора относительной скорости в относительном движении, и ускорения Кориолиса. харак­теризующего изменение вектора относительной скорости точки в пе­реносном движении и переносной скорости в относительном движении:

(5.45)

*

Вектор ускорения Кориолиса равен удвоенному векторному произ­ведению мгновенной угловой скорости вращения (поворота) подви­жной системы отсчета (угловой скорости переносного движения) на относительную скорость:

г“ 2й1Я. р х гОГп (5.46)

Рассмотрим, как определяются модуль и направление ускорения Кориолиса. Модуль определяется по правилу векторного произведения

И’, — ЗсОпррПвп, sin ф. (5.47)

где ф —угол между ыпср и vorH. ,

Формула (5.47) дает возможность установить случаи, когда ускорение Кориолиса обращается в нуль. Таких случаев может быть три:

1) <опср=0, это означает, что переносное движение отсутствует либо является поступательным, либо оно таково, что в данный момент его угловая скорость равна нулю;

2) г’,,™ = 0, это значит, что точка находится в состоянии от­носительного покоя либо относительное движение точки таково, что ее скорость в данный момент времени обращается в нуль;

3) ф = 0 или ф=180°, это значит, что относительное движение точки в данный момент происходит перпендикулярно к плоскости переносного вращения.

Направление вектора ускорения Кориолиса также находится в соот­ветствии с правилом векторного перемножения: он направлен пер­пендикулярно к плоскости, проведенной через векторы юпср и ёР1Н, 112 в сторону, откуда кратчайшее совмещение первого вектора со вторым видно происходящим против хода часовой стрелки (рис. 5.7).

Описанный в настоящем разделе математический аппарат сложного движения в бурении используется при рассмотрении движения частицы породы по шнековому транспортеру, при изучении процесса погруже­ния обсадных труб методом расходки и вращения, при рассмотрении кинематики катящейся по забою шарощки, при исследовании движения жидкости на вращающихся лопастях насосов и турбин и др.

Комментарии запрещены.