Бурение грунтовых зондов, установка энергетических колодцев

Кинематические цепи систем робототехники весьма разнообразны и, как правило, представляют собой так называемые незамкнутые пространственные^стержневые системы с несколькими сводами движе — ! ния, звенья которых соединены в различные низшие кинематические ‘ пары, причем требуемые относительные движения звеньев осуществ­ляются встроенными приводами. Представление о кинематических цепях роботосистем, как о ‘ незамкнутых цепях, условно вследствие того, что индивидуальные приводы звеньев образуют замкнутые 17 3477 257

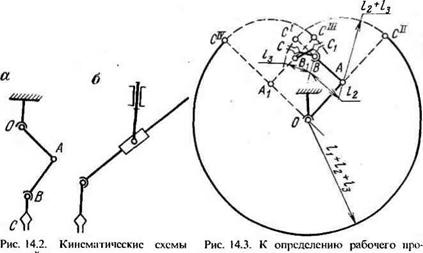
простоипix манипуляторов: а с последова гельно сферической, вра­щательной н сферической кинематичес­кими парами: <> с последовательно двумя вращаю. папами, поступательной и сферической нарами

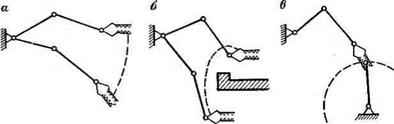
странства манипулятора

локальные кинематические цепи, т. е. механизмы, движение каждого из которых определяется одной обобщенной координатой. При наличии п звеньев с индивидуальными приводами для реализации простейших относительных движений такую робототехническую си­стему следует считать механизмом или машиной с п свободами движений.

Простейший пространственный манипулятор (рис. 14.2) состоит из трех подвижных звеньев, образующих последовательно сферичес­кую, вращательную и сферическую кинематические пары. Захват такого манипулятора обладает семью степенями свободы движения, не считая тех, которые свойственны самому механизму захвата. При необходимости обеспечения большого радиуса действия в схему манипулятора вводится поступательная кинематическая пара (рис. 14.2, б). Такой манипулятор имеет шесть степеней свободы движения, не считая собственно механизма захвата.

Для сравнительной оценки систем робототехники определены п» характерные свойства и параметры, к которым относят рабо1 ,е пространство, классификацию движений захвата, маневренность, зону обслуживания, угол и коэффициент сервиса, коэффициент возрастания скорости.

Рабочее пространство манипулятора и классификация движений схвата. Рабочим пространством манипулятора называют простран­ство, ограниченное поверхностью, огибающей все возможные пре­дельные положения звеньев манипулятора. Рабочее пространство 258

N

Ч

Рис. 14.4. Схемы движений манипуляторов в рабочем пространстве

/

/

должно определяться с учетом реальных конфигураций звеньев и их относительной подвижности. Приближенное представление о рабочем пространстве манипулятора может быть получено по его кинематичес­кой схеме. Так, рабочее пространство манипулятора, показанного на рис. 14.2, й, ограничивается снаружи частью сферы радиуса (рис. 14.3), равного сумме длин трех звеньев + /2 + /3 с центром в точке О и частью CnOC, v поверхности тора, образованной движением центра окружности радиуса /2 + /3 по окружности, проекция которой на плоскости отображается отрезком АА1. Внутри рабочее пространство ограничено конусной поверхностью АО A, и усеченной конусной поверхностью АВВ1А1. При этом учтены предельно до­пустимые углы относительного поворота звеньев. Для целей про­граммного управления движением роботосистем необходимо опре­делять уравнения граничных поверхностей рабочего пространства. К особенностям таких поверхностей относятся ограниченность их размеров и сложная структура.

Значительное количество свобод движения роботосистем дает возможность реализации различных движений внутри рабочих про­странств в зависимости от наличия или отсутствия препятствий. Можно выделить четыре класса таких движений. Первый класс включает движения звеньев роботосистемы, несущей свободный объект в свободном рабочем пространстве (рис. 14.4, а), второй — целенап­равленные движения захвата при наличии препятствий в рабочем пространстве (рис. 14.4, б), третий — движение звеньев в свободном рабочем пространстве при наложении связей на движение захваченного предмета (14.4, в), четвертый—движение звеньев при наличии препят­ствий в рабочем пространстве и связей, наложенных на движение захваченного предмета.

Маневренность роботосистем. Маневренностью роботосистем на­зывают свойство сохранять способность движения промежуточных между стойкой и захватом звеньев при неподвижном захвате. За меру маневренности принимают число свобод движения кинематиче­ской испн роботосистемы при неподвижном схвате. Например, маневренность манипулятора, показанною на рис 14.2. о. определяеюя

одной свободой движения — вращением диады АО—АВ вокруг оси! ОБ, а маневренность манипулятора, представленного на рис. 14.2, б,| определяется нулевой подвижностью звеньев. Маневренность робо-| тосистем может меняться с изменением последовательности рас-1 положения кинематических пар без изменения их общего числа. Так/! после взаимной перестановки кинематических пар А и В маневренность! манипулятора (см. рир. 14.2, а) ухудшается и определяется лишь Г возможностью вращения звена О А вокруг своей продольной оси/ Улучшение маневренности роботосистем позволяет реализовать движе­ния звеньев ’более высоких классов при изменении ситуации рабочих j пространств робототехники.

Зона обслуживания. Зоной обслуживания роботосистемой называют, пространство, каждая точка которого может быть достигнута схватом, например, точка С продольной оси ВС торцовой поверхностью губок 1 (см. рис. 14.2, а). Допускаемая при этом погрешность несущественна. Зона обслуживания может быть теперь определена, как множество возможных положений точки С схвата манипулятора. Например, зона обслуживания (сервиса) того же манипулятора ограничивается снаружи составной поверхностью, которая охватывает рабочее про­странство, а внутри — сферой, очерченной радиусом ОС, равным минимально возможному расстоянию между точками О и С. В за­висимости от размеров звеньев и допускаемых относительных пе­ремещений внутренняя граничная поверхность зоны обслуживания может быть и составной. В любом случае изложенный, выше метод применим и для аналитического представления поверхности.

Угол и коэффициент сервиса. Зона обслуживания не вполне определяет работоспособность роботосистем, так как расположение точки С схвата в зоне обслуживания еще не определяет возможную ориентацию схватоносителя в пространстве (звено ВС на рис. 14.2, а). Для оценки возможных положений схватоносителя мысленно фик — j сируем точку С, оставив за звеном ВС возможность вращения в любом направлении. С точки зрения кинематики механизмов это соответствует размещению в точке С сферической кинематической пары, неподвижным зерном которой будем считать захватываемый предмет. При этом механизм манипулятора превращается в замкнутый пространственный многозвенный механизм или жесткую систему звеньев. Если такой механизм обладает подвижностью, отличающейся! от нулевой, то звено ВС может рассматриваться как кривошип или j коромысло пространственного стержневого механизма, которые в своем возможном вращательном движении опишут некоторый телесный угол с вершиной С. Телесный угол |/, описываемый схватоносителем при его возможном движении в составе простран­ственного замкнутого механизма при условии лишения точки С схвата возможности поступательных перемещений, называется углом сервиса. Известно, что максимальное главное значение телесного угла соот­ветствует площади сферы единичного радиуса, или фтах = 4л. Если после фиксации точки С кинематическая цепь роботосистемы пре — 260

вратилась в неподвижную конструкцию, то, очевидно, угол сервиса ф = 0. Таким образом, приходим к заключению об области изменения угла сервиса: 0<ф<4л.

При сравнительной оценке роботосистем используют отношение действительного угла сервиса к максимально возможному. Отношение действительного угла сервиса роботосистемы в некоторой точке зоны обслуживания к предельно возможному его значению называют коэффициентом сервиса роботосистемы в данной точке зоны об­; служивания

О«0«1. (14.1)

Заметим, что поскольку размещение в точке С схвата сферической | пары — фиктивная операция, то ограничение относительных вращений

звеньев, образующих сферическую кинематическую пару, здесь не учитывается. Коэффициент сервиса определяет количественную сто­рону телесного угла, описываемого схватоносителем, но не отображает его форму. Для качественной оценки телесного угла, описываемого схватоносителем, вводят коэффициент формы телесного угла

v = vmin/vmax, * 0<v<l, (14.2)

где vmin и vmax—наименьший и наибольший углы плоских сечений телесного угла 0 с вершиной в точке С.

Аналитически угол сервиса роботосистемы можно определить по i следующему алгоритму.

1. Выбрать некоторую неподвижную систему координат, ориен­тированную относительно стойки (предпочтительно декартову про­странственную систему координат).

2. Составить эквивалентную кинематическую схему пространст­венного или плоского механизма исследуемой роботосистемы путем закрепления точки С схвата в произвольной точке С зоны об­: служивания с текущими координатами в выбранной системе координат

! (например, х, у, г).

3. Определить подвижность эквивалентного механизма по методу, ‘ изложенному, например, в работе [7].

4. Составить уравнения для определения параметров движения I схватоносителя по подходящему методу кинематического анализа

; механизмов. С целью упрощения решения задачи целесообразно

‘ разделить все линейные размеры геометрической схемы механизма

‘ на длину схватоносителя (приведение линейных’ величин к безраз-

■ мерному виду).

; 5. Решить составленную систему уравнений и определить так

называемую коромысловую кривую, описываемую начальной точкой схватонбсителя, которая, очевидно, будет кривой линией на сфере ; единичного радиуса лак функция параметров механизма и координат

точки С(л(. г.:. ic):

д = .(.’с, Гг, !с); J’c, zc); z = z(.’c, Vc, zc)- (14.3)

261

6. Воспользоваться формулой для определения площади единичной сферы, ограниченной полученной коромысловой кривой линией. Эта площадь и будет численно равна телесному углу ф в произвольной фиксированной точке С зоны обслуживания. Для вычисления телесного угла в конкретной точке достаточно в полученную формулу для определения ф подставить соответствующие значения координат хс, ‘< • "с-

{

7. Определить коэффициент сервиса 0, разделив телесный угол ф на 4л.

8. Исследовать на экстремум функцию ф = ф(лу, г<~, l() как

функцию трех переменных величин в замкнутой области, являющейся зоной обслуживания, для определения экстремальных значений угла сервиса исследуемой роботосистемы.

Все упомянутые выше параметры кинематических цепей роботов и манипуляторов, в том числе предназначенных для целей развед­очного бурения, определяются по заданным структурно-кинематиче­ской схеме и параметрам механизма, что составляет задачу струк­турно-кинематического анализа механизма.

Для целей проектирования роботосистемы, удовлетворяющей по­ставленным требованиям, должны быть заданы числовые значения упомянутых параметров, что будет являться основанием для решения задачи определения структуры и геометрических размеров механизмов. Эта задача относится к структурно-кинематическому синтезу механиз­ма, является достаточно сложной и должна решаться с использованием специальной литературы.

Комментарии запрещены.