Бурение грунтовых зондов, установка энергетических колодцев

В последнее время в практике бурения геологоразведочных скважин большого диаметра в крепких, породах начинает использовать колон­ковый породоразрушающий инструмент, оборудованный цилиндричес­кими шарошками. При вращении инструмента относительно оси скважины шарошки, обкатываясь по забою, разрушают его.

При создании надежного в работе и долговечного породораз — рушаюшего инструмента с цилиндрическими шарошками возникают многочисленные, требующие решения кинематические и динамические задачи. Одна из них будет рассмотрена ниже. Ее постановка и решение осуществлены автором. Сущность задачи сводится к определению полного ускорения различных точек шарошки. В последующем полученный результат использован автором для определения момента, возникающего в осях шарошки. Заметим, что тот же результат 124

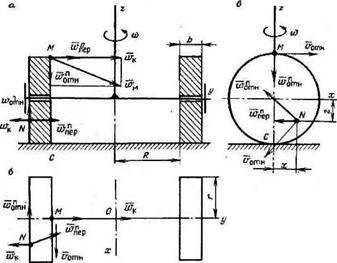
Рис. 5.11. Расчетная схема пары катящихся по забою цилиндрических шарошек

может быть получен на основе изучения гироскопических эффектов при движении шарошки.

Расчетная схема пары шарошек, вращающихся вокруг оси скважины — и собственной оси г. показана на рис. 5.11. Сформулируем задачу. Инструмент вращается в скважине с постоянной угловой частотой со. Шарошка представляет сплошной однородный диск радиусом г и шири — | ной Ь. Она обкатывается по забою без скольжения. Возникающим

скольжением, обусловленным различными линейными скоростями по ширине шарошки, пренебрегаем. Расстояние от оси скважины до точки I обкатывания С, представляющей собой мгновенный центр скоростей,

; равно R. Необходимо определить полное ускорение точки М,

1 находящейся на внутренней поверхности шарошки в крайнем верхнем

положении, и точки N, расположенной на внешней поверхности шарошки и удаленной от осей г и. т (рис. 5.11), в) на расстояние соответственно V и I. На рис: 5.11. а. див для наглядности показаны соответственно три проекции инструмента: фронтальный вид, план и боковой вид.

При решении задачи будем исходить из топ что каждая точка, обкатывающейся по забою шарошки, совершает сложное движение. С одной стороны, точка участвует вместе с осью шарошки во вращательном двйжении вокруг оси скважины (переносное движение), с другой—перемещается по окружности вокруг оси шарошки (от­носительное движение).

Полное ускорение любой точки шарошки может быть определено по формуле (5.48).

Сначала определим ускорение точки М.

• Относительная угловая скорость вращения шарошки определится как

иОТн = соЛ/г. (5.94)

Так же, как и переносная угловая скорость, относительная угловая скорость шарошки—величина постоянная. Поэтому две составляющие вектора полного ускорения обратятся в нуль:

И пег = о и и’Д™ = 0. (5.95)

Нормальная составляющая переносного ускорения

в’пср=ю2Л. (5.96)

Она проецируется в натуральную величину на фронтальном виде (рис. 5.11, о) и в плане (рис. 5.11,6).

Нормальная составляющая относительного ускорения

и’5тн = Юотн r=io*R*/r. (5.97)

Эта составляющая проецируется в натуральную величину на. фронтальном и боковом (рис. 5.11, в) видах.

Ускорение Кориолиса

и’„ = 2юготн sm ф. (5.98)

Так как г„.. = ы„..г=оз«. то sin ф = 1. тогда

\=2к>г R. (5.99)

Ускорение Кориолиса проецируется в натуральную величину на фронтальном виде и в плане.

Полное ускорение точки М

и«=К + "Л1/2 = [«о+и-.)2 + (-и-тв)2] 1/2 =—у—(Зг2+ R 2) ‘’2.

(5.100)

Определим ускорение точки N:

Ц’™Р=ю2 [(R+b)2 +.v2] 112. (5.101)

Эта составляющая проецируется в натуральную величину только на плане

. со2/?2 ,

<™=—^-(*2+z2)‘/2. (5.102)

Эта составляющая проецируется в натуральную величину только на боковом виде

H’„=2corOTHsincp1 (5.103)

, , ,,соR.

lte=,,UV } =—Ix^ + z4) (5.104)

stotfs^lzl/lJT+z4)1’4. (5.105)

Ускорение Кориолиса проецируется в натуральную величину на. фронтальном виде и плане.

II !

Тогда

Как видим,- ускорение Кориолиса точек шарошки не зависит от ширины шарошки, но зависит от координаты z. j Полное ускорение точки N найдем через его проекции на оси г х, у и z:

— 2

м>=— Jx2[R2 + riJ — + r1\K + b)r-2Kx~1+R*z*. (5.107)

г ‘ — —

Подставив соответствующие численные значения величин, по формуле (5.107) можно определить полное ускорение любой произ­вольно выбранной точки шарошки.

Обращаем внимание на одно важное обстоятельство. Ускорение • Кориолиса любой точки левой шарошки (фронтальный вид), нахо­

дящейся в верхней части шарошки, направлено к оси переносного вращения, в нижней части — от оси переносного вращения. Это обстоятельство неизбежно будет приводить к появлению динамичес­кого момента, стремящегося повернуть шарошку в плоскости zy против хода часовой стрелки.

Комментарии запрещены.