УСКОРЕНИЕ ТОЧКИ, ПЕРЕМЕЩАЮЩЕЙСЯ ПО ВРАЩАЮЩЕМУСЯ СТЕРЖНЮ (ТРУБКЕ)
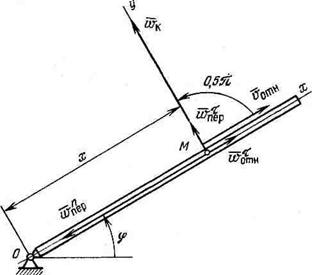
Данная задача позволяет наглядно проиллюстрировать изложен-, ный в разделах 5.5 и 5.6 материал и приобрести определенный навык в решении аналогичных и более сложных задач. Стержень (трубка) вращается в плоскости чертежа вокруг точки О против хода часовой стрелки по закону tp = f2/2 (рис. 5.9). Вдоль стержня (трубки) из точки О перемещается точка М по закону х=12. Найти модуль абсолютного ускорения точки М в момент времени tj = 2 с.
Аналогом этой задачи в бурении могут служить задачи о движении частицы горной породы по шнековому транспортеру, о движении частицы жидкости по лопатке гидротурбины и некоторые другие.
В рассматриваемом случае переносным движением является движение трубки, относительным—движение точки относительно трубки. Записываем выражение (5.48). Для определения первых двух составляющих абсолютного ускорения мысленно останавливаем относительное движение (движение точки М вдоль трубки). Кинематические характеристики будут иметь значения: е—=1с 2. д-=4 м, н’,г, ср=4 м -с-2, H’ncp = u>ncpv, u>„ep=d(p/dt, (оПСр = 2 с-1, и’"ср = 4- 4= 16 м — с~2.
Для определения двух вторых составляющих абсолютного ускорения мысленно останавливаем движение трубки. Соответственно woT« = d2/dt2 — 2 м — с-2, и’оТН = 0, поскольку относительное движение является прямолинейным, и’к = 2сопсрготн, и’к = 2-2-4=16м-с-2.
|
Рис. 5.9. Схема ускорений тонки, перемещающейся по вращающейся трубке |
На чертеже показываем все составляющие абсолютного ускорения. Касательная составляющая переносного ускорения направлена по касательной к окружности, описываемой точкой М вместе с трубкой, в сторону движения. Нормальная составляющая направлена вдоль трубки к точке О (центру вращения). Касательная составляющая относительного ускорения направлена вдоль трубки в сторону относительного движения точки М. Ускорение Кориолиса направлено перпендикулярно к трубке в сторону ее вращения.
Для определения модуля абсолютного ускорения можно воспользоваться методом проекций на оси х и у. На основании этого метода получим w = 24,4 м-с-2. По направляющим косинусам можно найти направление вектора ускорений.