Бурение грунтовых зондов, установка энергетических колодцев

Схемы сообщества, подобные той, что была при­ведена на рис. 42, можно встретить в любом учебнике морской биологии. Такие схемы нужны и полезны и в

технике, и в биологии, но они — лишь первый шаг к по­ниманию устройства и жизни сложной системы. Второй шаг —ее принципиальная схема. В радиотехнике это электрическая схема. Она удобна тем, что ее язык уни­версален. Универсальным должен быть и язык трофоди — намики, чтобы можно было описывать структуру и функ­ционирование биоценозов со всем разнообразием их связей. —

Раз любая живая система открыта и существует лишь благодаря непрерывному притоку и оттоку вещества и энергии (не зря говорят: «поточная система»), то ее в принципе можно описать в форме соответствующего кас­када: «падая» с одного трофического уровня на другой, вещество и связанная в нем энергия разделяются на не­сколько потоков. Основных потоков, существует три. По­ступившее на любой уровень вещество, во-первых, обра­зует биомассу своего уровня (Р), во-вторых, оно частич­но выделяется в виде конечных продуктов углеродного обмена —СОг, а свободная энергия, выделившаяся при этом, рассеивается в форме тепла (Т). В-третьих, вещес­тво выделяется в виде органических экскретов, хитино­вых покровов, отпадающих при линьке животных, и т. п.

(Е).

Например, для звена первичной продукции, где ве­щество синтезируется из углекислого газа. и воды при участии солнечной энергии, уравнение прихода и расхода по разным статьям бюджета имеет следующий вид:

‘ — Р-р+Т + Е, .

где Р — валовая продукция; р — чистая продукция, илв весовой, прирост биомассы; Т — траты вещества на дыха­ние и Е — прижизненное выделение органических мета­болитов. Все элементы уравнения можно измерить, вы­разив их в единицах количества углерода или в калори­ях, что будет одинаково универсально. Примерное чис­ленное соотношение элементов балансового равенства для первичных продуцентов таково: —

100 = 50р + 35Г+ Л5Е.

У гетеротрофных организмов существуют те же ос­новные входы и выходы, так что уравнение балансового равенства очень похоже на предыдущее:

или в примерном численном выражении:

100 = 30 р + 20 {Ех + Е2) + 50 Т,

где Р — продукция гетеротрофного уровня; р — потреб­ленная пища; Е—выделенные твердые отходы метабо­лизма, Е2 — выделенные, жидкие отходы метабо­лизма и Т — траты вещества на дыхание. Все входы и выходы также могут быть выражены в единицах количе­ства углерода или энергии. .

Сведения об отдельных трофических уровнях нетруд­но теперь объединить и применить их к описанию тро­фических цепей. Любая цепь, состоящая из первичных продуцентов (I), растительноядных (II) и поедающих их хищников (III), может быть представлена в виде кас­када «дырявых кастрюль»,.отверстия которых соотносят­ся друг с другом (в одной кастрюле), как соотносятся между собой статьи материально-энергетического бюд­жета организма (рис. 43). Заметим,- что в каждый ни-

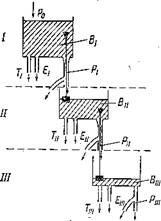
Рис. 43. Гидродинамиче­ская модель трофического каскада.

В — биомасса уровня, Р — прирост, Е~выделение экскретов, Т — траты на дыхание. Уровни: / — первичные продуценты (во­доросли), // — растительноядные животные,///—хищники, питаю­щиеся растительноядными жи­вотными.

жележащий уровень попадает лишь часть биомассы, син­тезированной на вышележащем уровне, так как значи­тельная часть организмов погибает и разлагается, не успевая быть съеденной.

Допустим, что из первой кастрюли во вторую, ниж­нюю, поток Pi выливается со скоростью 10 л/ч. Из вто­рой кастрюли в следующую также попадает лишь 1/3,

т. е. около 3,3 л/ч, а 2/3 отводятся в другие каналы (Гц і: /-‘п.) • .

Пусть по каналу Рщ из самой нижней кастрюли тоже оттекает лишь треть воды, т. е. около 1 л/ч, а 2/3 •отчуждаются по каналам Тщ и Ещ. Если сечения отвер­стий Pi, Рц и Рщ в кастрюлях равны между собой, то такое соотношение скоростей вытекающих потоков (10:3,3:1) возможно лишь в том случае, если вода в кастрюлях установится на уровнях, соотносящихся друг с другом как 100:10 :1. Действительно, по уравнению Торичелли, уровень воды в баке (К) связан со скоростью ее истечения из него (и) уравнением

‘ гі = %yr2gh,

. ^ ‘ • где и — потери на трение (ими в данном случае можно. пренебречь) и g — ускорение свободного падения. Из этого уравнения следует, что если уровни воды в баках. соотносятся как 100: 10 : 1, то скорости истечения отно­сятся как 10 : 3,3 : 1.

Такая гидродинамическая модель несколько упроща­ет картину, существующую в трофической цепи. В ней не учтены некоторые детали, а взятый числовой пример отражает лишь частный случай из многих весьма разно­образных соотношений параметров, которые наблюда­ются между уровнями трофической пирамиды в реаль­ных сообществах. Важно другое: модель принципиаль­но верно передает динамическую ситуацию, существую­щую в главном трофическом каскаде любого сложного сообщества, так как аналогом притекающей в кастрюли воды является либо углерод пищи, либо содержащаяся в пище энергия (на первом уровне это энергия солнца). Удельные скорости тока. воды через отверстия кастрюль («Р») аналогичны удельным скоростям продукции (обычно ее выражают в граммах продуцируемого орга­нического вещества на 1 г или 1 кг биомассы организ­мов этого уровня). Уровням воды в кастрюлях аналогич­ны биомассы организмов на каждом трофическом уровне ь сообщества. В соответствии с гидродинамической мо­делью каскада биомасса первичных продуцентов обычно в 5— 10 раз превышает биомассу травоядных, а биомас­са хищников соответственно ниже биомассы их пред­шественников по цепи. Величины удельной продукции организмов в последовательных трофических уровнях со­относятся между собой в таком же согласии с моделью.

Насколько верно в принципе предсказание модели относительно соотношения биомасс разных трофических уровней и скоростей продукции и насколько реальные их соотношения отличаются от теоретически возмож­ных, видно из нескольких примеров. По данным извест­ного океанолога В. Г. Богорова[35], соотношение биомасс рачков, обитающих в толще воды (зоопланктон), более крупных животных, обитающих на дне моря (бентос) и плавающих в воде крупных животных (нектон) в целом по Мировому океану равно 21:10:1 млрд. т. А годовая продукция тех же групп животных соотносится как 53:3:0,2. Отметим, что биомассы названных групп живот­ных находятся по отношению друг к другу примерно в том же положении, что и «дырявые кастрюли» в гидро­динамической модели. Таким образом, правило «пира­миды биомасс», вытекающее из этой модели, хорошо со­блюдается в море. Основание этой пирамиды — водорос­ли, служащие пищей всем животным. В биоценозах су­ши и пресных водах, а также в прибрежных морских биоценозах их биомасса намного выше биомассы жи­вотных, как это и предполагается гидродинамической моделью. Однако в целом по Мировому океану биомас­са водорослей равна, по данным В. Г. Богорова, всего 1,7 млрд. т, что значительно ниже общей биомассы мор­ских животных (32,5 млрд. т). Однако это количество водорослей вполне обеспечивает питание последующих уровней за счет очень высокой скорости продукции, ко­торая водорослям свойственна (550 млрд. т в год по сравнению со скоростью продукции всех животных, рав­ной 56 млрд. т в год). При определенных параметрах потоков воды такую картину можно получить и в гидро­динамической модели.

При всей своей наглядности гидродинамическая мо­дель малоудобна для научных целей. Более удобной бы­ла бы-электрическая модель. Но наиболее удобна мате­матическая модель, реализованная на ЭВМ. Такие мо­дели существуют, и их исследование дает интересные результаты. Институт океанологии АН СССР в те­чение нескольких лет разрабатывает под руководством

М. Е. Виноградова машинную модель потока энергии через пелагическое сообщество тропических районов Ти-‘ хого океана. Для этого используются данные, собирае­мые сотрудниками института во время экспедиций на известном научно-исследовательском судне «Витязь».

Но вернемся к «дырявым кастрюлям», чтобы сделать еще некоторые, выводы. Читатель, присмотревшийся к рисунку и его объяснению в тексте, поймет теперь, ка­ким, образом поточный характер системы, на первый взгляд исключающий как будто бы всякую стабильность, приводит к определенному соотношению биомасс орга­низмов на разных трофических уровнях, т. е. к опреде­ленной и стабильной структуре сообщества. ‘

На события в трофическом каскаде можно взглянуть и с точки зрения управления ими. Уровень II контроли­руется уровнями I и III, а уровень III уровнем II.

Если добавить к этому, что на каждом трофическом уровне находится обычно много разных видов, имеющих специфические особенности питания и продуцирования, то нетрудно понять, что возможности взаимной регуля­ции в трофических сетях весьма велики, о чем мы уже не раз говорили. Такую взаимную регуляцию в трофи­ческой цепи называют внутренним управлением.

Структуру трофической пирамиды можно выразить не только в единицах количества вещества, но и в кало­риях, заключенных в нем, в калориях на кубометр воды или на квадратный метр поверхности дна, если речь идет об организмах донных. Вот один конкретный пример:

Энергия чистой		Энергия в звене
первичной		травоядных
продукции		животных
15		1,5

Энергия в звене хищников, питающихся травоядными 0,15

калорий на 1 м3 поверхности дна в сутки.

ч Этот пример опять-таки отражает лишь один из мно­гих возможных случаев. В различных сообществах соот­ношение запасов энергии на разных уровнях различает­ся, однако «закон пирамиды» остается неизменным, от­ражая основную черту структуры сообщества. ;

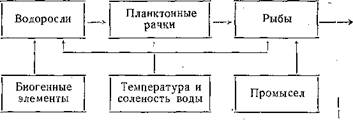
Чем же вызываются различия в трофической струк­туре разных сообществ? Прежде всего разнообразием

конкретных условий среды, существующих в разных мо­рях и районах океана. Например, в одних районах мощ­ный подъем глубинных вод, содержащих большой запас биогенных элементов, необходимых для успешного фо­тосинтеза, вызывает интенсивный рост биомассы водо­рослей. А в других — биомасса мидий на отмели, воз­можно, из-за дополнительных источников пищи (напри­мер, приносимый из других сообществ детрит) оказы­вается выше «нормы».

На каждом трофическом уровне действуют свои оп­ределяющие его биомассу многочисленные внешние фак­торы, образующие внешнее управление звеном или тро­пической цепью, например:

внешние управляющие факторы

В звене первичной продукции ими могут быть не только биогенные элементы, но и интенсивность света, й температура. На всех уровнях каскада это может быть температурный фактор или соленость воды, а на уровне рыб — и заболевания рыб, и массовая гибель из-за раз­ных внешних причин, и промысел. Несколько забегая вперед, скажем, что разнообразие факторов, влияющих на продукцию каждого уровня как раз и позволяет ис­кусственно видоизменять природные системы в сторону, выгодную человеку. Принцип внешнего управления — также одно из основных средств в планировании и созда­нии искусственных морских ферм. Например, в каком — нибудь заливе можно систематически вносить в воду биогенные элементы, стимулируя первичную продукцию, а на этой основе и последующие звенья пищевой цепи. Такие фермы уже создаются, биогенные элементы вно­сятся с бытовыми сточными водами — одновременно ре­шаются две проблемы: пищевая и сточных вод. Биологи должны учитывать влияние внешних факторов не толь­ко для промысловых целей, но и для изучения1 природ­ных продукционных систем. Вот пример модели, предло­женной для звена фитопланктона известным американ­ским океанографом Гордоном Райли. Она показывает выедание фитопланктона растительноядными животны­ми, связь его продукции с потоком ассимилируемой энергии и такими факторами, как турбулентность вод­ных масс и концентрация биогенных элементов:. ‘

где Р — популяция фитопланктона на единицу объема воды; Рн — фотосинтетический коэффициент, являющий­ся функцией освещенности, поглощения света водой и концентрации биогенных элементов, а также турбулент­ности воды; RP — дыхание фитопланктона с коррек­цией на температуру воды и # —коэффициент выедания фитопланктона, пропорциональный плотности популяции растительноядных животных. Хотя эта модель учитыва­ет не все факторы, влияющие на продукцию фитопланк­тона, она дает результаты, близкие к реальным событи­ям, связанным с динамикой фитопланктона (см. рис. 1).

Для зоопланктона, питающегося водорослями, анало­гичное уравнение выглядит так:

—Щ— = Н(А — R — С — D),

где Я -— популяция зоопланктона, А — коэффициент выедания им фитопланктона, пропорциональный биомас­се последнего до величны 8% веса тела животных в день, R — дыхание зоопланктона, С — выедание зоо­планктона хищниками следующего уровня и D — есте­ственное отмирание рачков.

Но вернемся к вопросу об управлении структурой и параметрами пищевых цепей в биоценозах. Возможно­сти воздействовать на них лежат не только в использо­вании таких абиотических факторов, как свет, темпера­тура, концентрация биогенных элементов (которые мож­но в той или иной мере задавать в условиях морских ферм). Можно изменять и структуру самой пищевой це­пи, вставляя в нее некоторые «искусственные» элемен­ты. Пример таких воздействий — успешные результаты акклиматизации животных — перенесения ценных для че­ловека видов из одного моря в другое. Так, можно со­слаться на удачное переселение одного из дальневосточ­ных видов лосося — горбуши — в Баренцево море. На­чатый около 10 лет назад этот большой эксперимент (на нескольких реках Кольского полуострова, впадающих в Баренцево море, были построены специальные хозяй­ства для выращивания мальков из икры’—«рыбовод­ные з&воды») привел к тому, что теперь здесь. начат промышленный лов горбуши. Точно так же из Азовского моря в Каспийское успешно переселяли кефаль. В пос­левоенные годы в научных журналах и газетах писали об удачном переселении другой группы организмов —- беспозвоночных: в Каспийское море были завезены it прижились там нереисы, служащие хорошим кормом для рыб. Проводятся такие работы и за рубежом. Боль­шую пользу принесло переселение одного вида сельди из Атлантического океана в Тихий. Акклиматизация при­носит хорошие результаты только в том случае, если переселяемый вид «вписывается» в новом водоеме и в существующую там пищевую сеть, и в окружающие аби­отические условия. И если до сих пор вселение новых видов базировалось не столько на теории пищевых це­пей, сколько на общих представлениях о жизни и жиз­ненных потребностях переселяемых видов, то в будущем оно станет опираться именно на теорию. Тогда можно будет не только заранее предвидеть — приживется пе­реселенец или нет, но и предсказать, какова будет его возможная биомасса и скорость продукции в новых ус­ловиях, как его вселение повлияет на структуру других элементов пищевой сети.

Комментарии запрещены.