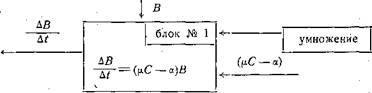Бурение грунтовых зондов, установка энергетических колодцев

Морские биологические системы очень сложны. Но элементы, из которых они состоят, условно можно считать простыми. Сложные системы ученые изучают на их моделях. Чтобы построить. модель, необходимо знание символов элементов, символов их связей друг с другом и их простых свойств. Необходимо также уме­ние оперировать этими символами, соединяя их тем или иным образом и используя результаты такого соедине­ния. Возьмем простейшую биологическую систему, счи­тая ее «элементарной», и проследим последовательные этапы ее описания на разных языках, широко приме-

няемых в науке. Мы можем пройти путь от азбуки сим­волов к их соединению в определенные научные поня­тия и до введения их в электронно-вычислительную ма­шину (ЭВМ). Машина сделает Самую трудоемкую ра­боту— произведет необходимые расчеты. Обсуждение результата завершит логику исследования нашей эле­ментарной системы. ‘

Что же считать самым элементарным в насыщенном жизнью океане? Организм? Это кажется самым естест­венным. Но один организм, взятый сам по себе, так же мало характеризует события в океане, как мало пере­дает мысль человека одно слово, случайно выхваченное из его речи. Чтобы понять мысль, нужно услышать хотя бы несколько сказанных им фраз — совокупностей слов. Начнем поэтому рассказ о живых системах моря не с организма, а с популяции организмов. Она и будет на­шим «элементарным» объектом.

Популяция — это совокупность особей одного вида, находящихся на данной территории и имеющих возмож­ность общатпся друг с другом (например, для встречи брачных пар). Популяцией является и «облако» клетокч какой-нибудь одноклеточной водоросли, парящее в тол­ще воды, и группа морских ежей на дне. Жизнь попу­ляции—прежде всего ее питание, рост и воспроизвод­ство себе подобных. і

Водоросли питаются, потребляя в качестве источника углерода растворенные в воде карбонаты и используя энергию солнечного света. Ежи поедают растущие ря­дом многоклеточные, водоросли, черпая из них углерод и энергию.

Но питание это только «вход» системы. На ее «вы­ходе» — продукты жизнедеятельности (метаболиты). У водорослей — кислород и растворенные органические. соединения, выделяемые ими в воду. У ежей — углекис­лота и тоже органические выделения — твердые и раст­воренные..Зная «вход» и «выход» популяции, можно про­следить за ее ростом. Начнем с того, что изобразим графически популяцию, ее пищу и выделяемые ею ме­таболиты:

получим то, что принято называть блок-схемой:

Соединив эти символы стрелками, т.. е. значками про­цессов

Потребление ■ Выделение пищи ■ метаболитов

Естественно, что чем больше биомасса популяции, тем больше она потребляет пищи. Графически это по­казано дополнительной стрелкой, идущей от биомассы к потреблению. Знак «-)-» у стрелки показывает, что связь положительна, т. е. усиливает рост биомассы.

Но эту же систему можно описать с помощью дру­гого языка;— математического. Для этого нам придется обозначить все элементы системы определенными (ко­нечно, произвольными) буквами:

концентрация пищи в объеме воды (мг/л) — С, концентрация биомассы в объеме воды (мг/л)—В, концентрация выделенных метаболитов (мг/л)—М. Введем символические изображения процессов: удельная скорость потребления пищи (л/(мг-сут­ки)) — |Д,

удельная скорость выделения метаболитов (1/сут­ки) — а[29].

Пусть dB — прирост биомассы за бесконечно малый отрезок времени dt. Ясно, что скорость изменения био­массы dB/dt равна разности между скоростью потреб­ления пищи цВС и скоростью выделения метаболитов а В. Следовательно, баланс выразится уравнением

-^- = рВС-аВ = (?С-*)В. (102)

Решение этого ур-авнения известно и его МОЖНО найти в любом справочнике: .

В = Вйе^с~«». (103)

Здесь буквой В0 обозначена биомасса в начальный момент времени. Графически последнее изображение

системы выглядит как___________

бесконечно восходящая —йг-гЕ.,

кривая. —

Описание системы с 1

помощью буквенных сим — .

волов намного богаче и _г — :

А

совершеннее описания, —~L-~^

сделанного языком блок — схемы. Пользуясь форму­лой (103), можно рассчи­тать, например, какова будет биомасса бактерий — через 10 суток, если их исходная биомасса равна 1-Ю-5 мг/л и если — они растут в благоприятных условиях, когда (цС — а) достигает 10 .сут.-1. На­ходим В = 1 • 10-5 ■ е10′ 10=

= 1038 мг/л = 1029 т — и это в одном литре! Через несколько дней неограни­ченного роста биомасса Рис. 35. Модель экспоненциалы ‘ бактерий превысит массу ного роста популяции.

ГплцТТЯІ Гтпаннпр ТТППРТТР / — бесконечно большой источник

солнца! странное поведе — пищи. 2— «концентрация» пищи, ко-

ние! Позже МЫ еще вер — ™Рая благодаря поплавку с затычкой

4 поддерживается всегда постоянной;’ НЄМСЯ К Нему. з — биомасса, поплавок с затычкой

Но И ТО И ДРУГОе ОГГИ — ‘■* —■110л0ЖИтельная обратная связь,

’ гJ Самописец 6, соединенный с поплав-

СЗНИЯ НЄ ПОКЭЗЫВЯЮТ НЄ — ком, рисует изменение биомассы.

прерывного изменения

биомассы. Чтобы график роста популяции получался из модели сам собою, без расчета вручную по уравнению, можно, построить «техническую модель», заменив потоки пищи и выделений, например, потоком воды или элек­трическим потоком (рис. 35).

Такая замена возможна, потому что, хотя пища и рыделеция химически различны, те и другие содержат

углерод и могут быть рассчитаны в одинаковых еди­ницах, как и электрический ток, на входе и выходе модели. Если техническую модель соединить с само­писцами, то тот же результат — неограниченный рост по­пуляции—будет получен автоматически, непосредствен­но из работающей модели, что весьма удобно. _

Работающую модель можно получить и совершен­но иным путем, самым быстрым и самым современ­ным— с помощью ЭВМ. Такой путь позволяет изучать очень сложные системы, не строя каждый раз громозд­кую техническую модель. Но прежде чем поручить та­кую работу машине, попробуем разобраться, что, собст­венно говоря, машина станет делать. Как и в техниче­ской модели, машине необходимо прослеживать процесс во времени. Для этого она будет отмеривать его с опре­деленными интервалами времени At, величину которых зададим.

Для первого интервала Ati = t — to рассчитаем на основе уравнения (102) конечную разность биомасс: ABi = Bi — В0. Заменим уравнение (102) приблизительно эквивалентным ему уравнением, но составленным из ко­нечных разностей времени и биомассы:

В і — В0 ABj / /^» d

—t=t=-Air = ^C-^B о-

Такой метод приближенного численного решения диф­ференциальных уравнений так и называется — решение в конечных разностях. Отсюда прирост биомассы ABi, за время A^i равен

ДВ^^С^а)^!, (104)

а величина биомассы В і ко времени t будет равна

Вх — BQ— A-fij = + (IаС — а)В0А^. (104′)

Затем Возьмем следующий конечный интервал вре­мени At2=t2 — t и проделаем то же самое, вставляя в уравнение (104") значение биомассы В, полученное на предыдущем шаге вычислений. Получим значение В2 для времени f2:

В2= Во -|- ДІ? і “Ь ДВ% — Во “Ь а) Я0Д*1 +

— +([АС-а)51Д/2. (104")

Потом проделаем точно такие же шаги по времени із, U, U, … Это весьма трудоемкая и однообразная ра­

бота: интервалы должны быть очень малы, а стало быть «шагов», или расчетных циклов, будет очень много. На­пример, чтобы просчитать рост популяции за 10 суток с интервалом 0,1 суток, необходимо 100 шагов. Рацио­нальнее поручить такой расчет машине, четко сформу­лировав стоящую перед ней задачу. Для этого с языка привычных понятий и буквенных символов надо перейти на язык машины.

Не нужно пугаться слов «машинный язык». Каж­дый, кто проделал описанные выше операции, уже поч­ти способен использовать вычислительную машину, по­тому что «для ЭВМ.» важно «знать» одно — логику только что проделанных операций. Теперь надо лишь составить правило, по которому мы только что считали (математики называют его алгоритмом). А полную программу действий для машины можно просто опи­сать на любом языке (русском, английском — она сама переведет программу на свой собственный язык) или нарисовать’ последовательность действий на бумаге. Итак, в чем же заключается правило счета? Проследим его последовательно. • ■

Этап 1. Как читатель помнит, умножались имеющи­еся у нас значения В на (р, С—а) и по уравнению (104) на каждом шаге получалось значение AB/At. Нарису­ем эту операцию схематически:

Получился первый элементарный блок действий (блок №1).

Этап 2. Потом полученное значение А В/ At умножа­ли на At, получая АВ, и. прибавляли к начальному В0 сумму всех А В, Шагая по времени от 0 до какого-то t, например до £=10, т. е. сумму (AB/At)At при t от 0 до 10. Суммирование так и запишем сокращенно, обо­значив пределы интервала времени: начало — под зна­ю

ком сигмы 2, а корец— над нею 2 , или все вместе:

. . … (=9 . ‘ ‘ ■ ” .

2 (^7") Правда, дальновиднее написать в более ^ / д в

общей форме: Б(-д7) Д^> так как считать, может быть,

придется не до времени 10 суток, а до — 20 или 30 или вообще до времени t. ‘

Теперь изобразим все сказанное графически — и го­тов блок № 2:

суммирование

, о В0

	блок № 2
во+Т( ‘ • 0	~кг)“

А В A t

Для случаев, когда суммируются бесконечно малые приращения, англичане предложили в свое время сим­вол суммирования — английскую букву S вместо гре­ческой сигмы Б. При скорописи буква S с обозначени-

t t

ем пределов J переродилась в знак f — интеграл. Ес­’ о. о

ли использовать аналоговую машину или допустить, что цифровая ЭВМ может считать с бесконечно малым шагом времени dt, то знак суммы в блоке № 2 заменит­ся на знак интеграла

. о Во, — ‘

I ■ : —

	блок № 2
В0+ J( 0	dS, dt )dt

лв

• dt

интегрирование

В

Этап 3. Соединим вместе блок № 1 — умножение и блок № 2 — интегрирование. Получится замкнутый цикл — блок-схема модели популяции (рис. 36). Не­трудно увидеть, насколько она богаче той, которая ри­совалась нами ранее, в более простых символах: стои­ло над нею поработать, : ‘

dB dt

Елок N2, интегрирование

Выход

Блок N1, умножение

— Ввод I цс-4

(рС-а)В

Рис. 36. Блок-схема модели популяции.

Во

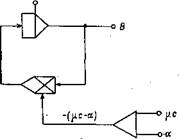
■ і. ‘ ■ " Рис. 37-. Блок-схема решения урав­нения (102) на аналоговой вычис­лительной машине.

Теперь, с этой блок-схемой можно уже и обращаться к специалисту, работающему на ЭВМ. Если машина ана­логовая, то на ней просто подбираются электрические блоки, соответствующие, аналогичные блокам в блок-схеме. В таком слу­чае программист перери­сует нашу блок-схему, заменив квадратики с на­писанными в них дейст­виями равнозначными и ■ наглядными символами.

Например, вместо блока умножения будет нарисо­ван символ

Вместо блока интегрирования будет нарисован символ

Во

Сверху — ввод начальных данных В0.

Операции, выполняемые решающими устройствами (блоками] аналоговых вычислительных машин, и их условные обозначения

/ Блок Операция Условное обозначение Блок умно­жения Генератор функций ^вых = 0,01 £/Вх, і X. X ^вх» 2 Воспроизведение не­линейных зависимо^ СТЄЙ С/вых = ^(£/вх) Увх,1 ° _L_ ^вьіх ‘Jex,2 ° ^вж°— F(U)’y>~0 ибьх

Вся блок-схема для моделирования будет теперь мак­симально проста, и ее легко составить и прочитать (рис. 37). Точно так же ее можно дополнять символами других операций, которые будут нужны при анализе бо­лее сложных систем. Символы можно взять из табл. 2.

Но чаще обращаются не к аналоговой, а к цифро­вой ЭВМ. Форма обращения к ней другая, но не слож­нее той, которую мы только что описали, так как это основа всего — лишь логический путь ваших собственных действий, высказанный другим языком. У каждого вида машин, как у каждой нации людей, свой собственный язык. Но, кроме того, разработано несколько универ­сальных языков, самый распространенный из них — АЛГОЛ (ALGOrithmic Language — алгоритмический язык), и каждая машина имеет, специально составлен­ную программу-переводчик, называемую ‘транслято­ром (Translation — переводить), с помощью которой она понимает АЛГОЛ. Для аналоговой машины про­грамма действия записывается графически, а для циф — , ровой — словами. Расскажем ее сначала подробно для ч себя. Машина буквально все «схватывает на лету». Ей не нужно длинных фраз, а достаточно одного-двух слов, но зато самых главных, выражающих суть ко­манды. Будем в наших фразах такие слова подчерки^ ват и в скобках давать либо их буквальный англий­ский перевод, либо их символическое изображение. И то, и другое можно взять из табл. 3.,Параметры же, с которыми машина будет оперировать, выделим, напи­сав их заглавными буквами. Потом составим только из

этих английских слов, символов и параметров про­грамму действий для машины.

— Разговор с машиной надо начать с сообщения о том, что она должна: —

1. Начать (begin) группу действий, о которых она узнает, читая нашу программу действий дальше. За­помним сразу, что в самом конце мы должны будем ей сказать и о том,, что пора закончить все действия. Команда на операцию начать называется: операторные скобки. Это напоминает арифметические скобки: мы

открываем скобки, пишем арифметические выражения внутри и потом закрываем их. Заметим, что внутри од­них скобок могут находиться другие. ..

Таблица 3 Изображение некоторых основных символов языка АЛГОЛ array массив begin начать do делать (цикл) end конец for для integer целый procedure операция real вещественный step шаг until (пока’не’…) до : = присвоить значение X умножить <  меньше « меньше или равно = . равно >  больше больше или равно Ф не равно

2. Дальше мы должны перечислить все величины, с которыми машине предстоит оперировать, и пояснить, что это за величины. Одни величины могут быть любы­ми, какие только встречаются в реальной действитель­ности, т. е. действительными (real) — например, целые числа, дроби и т. д. Другие могут принимать значения только целые (integer)—например, число живых ор­ганизмов в популяции может быть равно 1, 2, 3,…, но не 3/4 организма. Третьи величины, возможно, потре­буется собрать в один массив ( array) под одной бук­вой, но с разными индексами. Например: метаболиты одного вида Мь метаболиты другого вида М2, третьего вида М3 и т. д., скажем до 12 видов. В таком случае это массив (array) М (/1:12/).

3. Теперь машина должна ознакомиться со схемой основной операции (procedure), по которой ей придет­ся многократно считать, — операции ИНТЕГРИРОВА­НИЯ. Такие схемы хорошо известны, стандартизирова­ны и их можно выписать без изменений из справочни­ка. Выберем, например, наиболее часто используемый метод Рунге — Кутта.

4. Надо присвоить (: = ) нашим величинам, какие-то определенные исходные значения. Например, величине БИОМАССА В (в единицах мг/л) присвоить значение

0. 00001 (В:= 0.00001) и т. д. (в десятичных дробях ставится точка, а не запятая).

_ При постоянном изменении исходных значений вели­чин их ввод (input) лучше осуществить отдельно, напри­мер, после ознакомления машины с программой.

5. Далее необходимо сообщить машине, что выпол-. нять она будет циклические, т. е. одни и те же опера­ции многократно: для ВРЕМЕНИ Т, которому мы при­своили значение, например, 0.02 (будем использовать единицы времени — сутки) с шагом, например, 0.02, по­ка не достигнем такого-то времени, например, 10 суток, делай цикл. Используя табл. 3, слова этого приказа машине запишем так: for Т: = 0.02 step 0,02 until 10 do.

6. Теперь машина знает, каким образом работа рас­падается на циклы, но еще не знает, какова полная группа действий внутри цикла. Поставим снова опера­торные скобки и прикажем начать (begin) с умноже­ния. Результат умножения — это изменение биомассы (обозначим эту величину символом 1ZM) за один шаг:

IZM : = ([і. X С — а) X В. .

Не забудем внести эту реальную величину в началь­ный ознакомительный список (см. пункт 2). Дальше машина должна, как мы помним, выполнить операцию ИНТЕГРИРОВАНИЕ; сократим это длинное слово до символа INT. В скобках при этом символе укажем ве­личину, которую мы получаем, и выражение, которое

вводилось в блок интегрирования. Все вместе: INT (В, IZM).

Теперь интересующую нас величину надо дать на выход (output) из машины и указать, что надо отпеча­тать одновременно и время, к которому эта величина ‘ была достигнута: output (В, Т). На этом — конец (end) одного цикла. Когда же машина проделает заданное условием пункта 5 необходимое количество циклов, то можно считать, что она выполнила все, что от нее тре­бовалось, и программа закончена. Поэтому последней командой будет:.

7. Конец (end) программы.

Остается только выписать все выдел&нные нами слова, символы, цифры •— и АЛГОЛ-программа для ЭВМ готова[30]. Поскольку мы определяем биомассу, на­зовем программу «ВЮ-1». ■ .

АЛГОЛ-программа «ВЮ-1».

Begin

real Т, В, С, (a, a, IZM; —

, Procedure INT (переписываем стандартную опе­рацию из справочника)

В: =0.00001; С: = 2; р.: = 17; а: = 24;

for Т: = 0.02 step 0.02 until 10 do

begin IZM: = (і* X С— а) X B; INT (B, IZM);

output (T, B); end t end

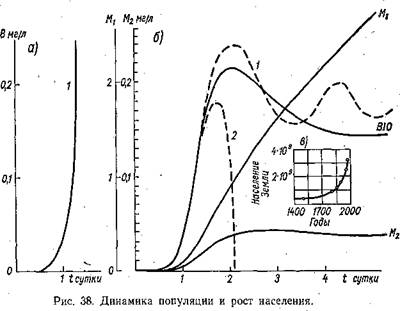
На рис. 38 а в виде кривой представлен результат реализации нашей программы «ВЮ-1». В. Н. Егоровым (Институт биологии южных морей) на ЭВМ «Минск-22». Меньше чем через минуту после начала счета машина прекратила печатать результаты и отказалась считать дальше, так как получаемые величины биомассы превы­шают сколько-нибудь разумные значения. Взрыв, насто­ящий взрыв биомассы! Опытный человек, только бросив взгляд на блок-схему, сразу же сказал бы, что система

совершенно неустойчива, она придет к взрыву, потому что в схеме есть положительная обратная связь — залог автокатализа, самоускорения, взрыва, но нет «сдерживающих центров». Атомный врыв, взрыв взрыв­чатых веществ, воспламенение горючих смесей и мно­гие, многие другие — все это процессы с положительной обратной связью, динамика этих систем точно описыва­ется именно уравнением (102).

а — расчет по программе ВІО-Г: / — биомасса популяции; б — расчет по программе BIO-2: биомасса популяции: BIO — п£и отводе метаболитов М2 с константой скорости А&—1; / — при отводе М2 с Ав>1; 2 — при отводе Ма с &s< 1; Ліі и М2 — метаболиты; в — рост населения земного шара.

Рост популяции организмов без вмешательства сдер­живающих факторов был бы аналогичен атомному взры­ву илц взрыву воспламеняющихся смесей — здесь тот же разветвленно-цешюй механизм и то же обратное по­ложительное воздействие продуктов реакций — биоло­гических в одном случае, физических и химических в других.

В действительности, как хорошо известно, рост био­массы популяции с определенного момента начинает

замедляться и наконец затухает совсем, или даже сни­жается. Реальный рост биомассы выражается S-образной кривой аналогично вырожденно-разветвленным цепным химическим реакциям (Он так и называется «S-образный рост»). ‘

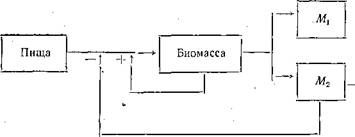
Причины замедления и прекращения роста популя­ции разнообразны, но изучены еще недостаточно. Боль­шое значение имеет исчерпание пищевых и энергети­ческих ресурсов и другие. Во всяком-случае одна из ^них — накопление в среде продуктов жизнедеятель­ности организмов. Например, хорошо известно, что при спиртовом брожении накопление в среде спирта посте­пенно приостанавливает процесс. То же самое касается и морских бактерий, и морских водОрослей, и живот­ных — с той лишь разницей, что выделения, тормозящие их рост, иные. В общей форме торможение роста про­дуктами жизнедеятельности выражается схемой с отри­цательной Обратной связью.

1

На схеме показан случай, когда первым тормозящим факторОм (ингибитором роста) является продукт М2. Но если этот продукт быстро отводится из среды, а остает­ся лишь Мь то ингибитором роста стал бы именно он. : ■

— Нам теперь ничего не стоит довести эту схему до ста­дии моделирования, вплоть до ЭВМ. Пусть мы решили воспользоваться цифровой вычислительной машиной, скажем, той же самой «Минск-22». Мы теперь отлично понимаем," что в разговоре с машиной математика, во — обще-то говоря, ни при чем и что ЭВМ — это не атри­бут математики, а мощное оружие в руках любого ис­следователя. Чтобы подчеркнуть это, избежим «буквён-

ных» формул (хотя они компактнее), а запишем все просто привычными нам словами, выделяя в каждом по­нятии первые две-три буквы, с тем, чтобы потом исполь­зовать в программе не целиком слово, а несколько букв. Итак, по схеме: .

1. ИЗМенение 1 биомассы = БИОмассаХ(ПОТребле — ние — ВЫДеление — СМЕРтность); Потребление = Ко­эффициент X ОРГаника X (1 + Коэффициент 2 X Ме­таболит 2);

2. ИЗМенение 2 метаболита 1 = Коэффициент З X X БИОмасса X ВЫДеление;

3. ИЗМенение 3 метаболита 2 = Коэффициент 4ХВИО- массаХВЫДеление — Коэффициент БХМЕТаболит 2.

Все-таки гораздо лучше записывать в «математичес­ком» виде! Но закончим так, заменив русский шрифт латинским, так как большинство трансляторов для циф­ровых машин требует латинских букв. Например, от слова ИЗМенение 2 вместо выделенного сокращения ИЗМ2 напишем: IZM2; вместо Потребление напишем РОТ и т. д. Составим, используя эти обозначения вели­чин, программу-для ЭВМ на АЛГОЛЕ, как АЛГОЛ — программу «ВЮ-1», и назовем ее «ВЮ-2». Выпишем из справочника или из учебника по программированию1 со­держание операции интегрирования по Рунге — Кутту, учитывая, что содержание процедуры — это группа дей­ствий, которые надо взять в операторные скобки begin… end. Кроме того, внесем еще два мелких изменения, по­скольку используемый транслятор «Минска-22» требует не подчеркивания команды, а постановки знака апост­рофа (’. . … ’). ПРИ команде выдачи на печать ре­зультатов использования не термина output, а слова STANDARD. При нем в скобках указывается цифрами, через сколько интервалов надо печатать результаты на листе, перфоленте и как их там расположить. С учетом всего этого и распишем программу. Мы записали ее не самым оптимальным и красивым способом; заботясь об одном: лишь бы было просто и понятно нам и ЭВМ.,

‘Г у тер Р. С.. Р е з н и к о в с к и й П. Т., Резник С. М. Программирование и вычислительная математика, вып. 1, вып. 2. М., «Наука», 1971. — — — — — . . _ . .

Алгол-программа BIO-2

’BEGIN’ ’REAL’ T, BIO, ORG, WYD, SMER, POT, Ml, М2, Kl, K2, КЗ, K4, K5;

’ARRAY’ IZM (11 :3 I);

’PROCEDURE’ INT (Y, F); ’REAL’ Y, F;

’BEGIN’— переписываем стандартную процедуру из справочника, например — ’REAL’ PI, Р2, РЗ/ Р4, Yl; PI :=0.02XF; Y1 : = Y;

Y: = Yl+Pl/2; P2:=0.02XF; Y: = Y14-P2/2; P3: =0.02 X F; Y: = Y1 + P3; P4: = 0.02XF;

Y: = Y1 + (P1 +2XP2 + 2XP3 + P4)/6;

’END’;

Kl : = 20; К2: = Ю; КЗ: =0.6; K4:=0.4; K5: = l; BIO: =0.00001;

ORG: = 2; SMER: = 2; M1: = 0; M2:=0;

’FOR’ T: = 0.02 ’STEP’ 0.02 ’UNTIL’ 5.1 ’DO’ ’BEGIN’ POT: = K1 XORG/(l+K2XМ2);

WYD : = 0.7 X POT+ 0.5; ■

IZM (11 I): = BIO X (POT — WYD — SMER);

IZM (121): = КЗ X WYD X BIO;

IZM(|3|): = K4X WYDXBIO —K5XM2;

INT (BIO, IZM (111)); INT (Ml, IZM (121));

INT (М2, IZM (IЗI));

STANDARD (”18”, ”10”, ”3”, T, ”30”, ”6”, BIO, ”50”, ”6”, Ml, ”70”, ”6”, М2);

’END’; .

’END’ .

Среди результатов расчета, выполненного ЭВМ, нас будет интересовать: 1) изменение биомассы популяции,

2) изменение концентрации первого метаболита М и 3) изменение концентрации второго метаболита М2. Эти па­раметры и просим машину выдать на печать.

Будем считать, что среди выделений организмов каж­дый из метаболитов М и М2 составляет определенную долю, токсичный метаболит М2 отводится из системы со скоростью, пропорциональной его наличной концент-

радии, и он угнетает организмы, снижая активность потребления ими пищи, и увеличивает их смерт­ность. .

На рис. 38 б приводятся результаты реализации на­шей программы «В 10-2» А. В. Леоновым (Государствен­ный океанографический институт) на ЭВМ «Минск-22М». Ход изменения биомассы популяции, изображенный на рисунке кривой ВЮ, в точности соответствует наблюдае­мой в опытах картине.

В этой программе мы приняли, что метаболит М2 от­водится из системы с константой скорости К& = 1. Если он отводится быстрее {Ks>iy, то развитие популяции соответствует кривой 1 и представляет собой затухаю­щие колебания. Со временем величина биомассы устано­вится на определенном уровне, как это происходит и в случае представляемой кривой ВЮ. Если метаболит 2 отводится очень медленно (/(5 <1 или /С5 ~ 0), то по­пуляция очень быстро погибнет (кривая 2).

В начальных участках кривых нет заметного при­роста биомассы популяции. Подобное состояние назы­вают лаг-фазой. Затем наступает фаза экспоненциаль-^ ного роста — взрывного, автокаталитического. В начале Э|Той фазы при низкой концентрации организмов влия­ние популяции на среду своего обитания ничтожно, и популяция развивается так же точно, как и в случае, когда отрицательного обратного воздействия метаболи­тов не было, — взрывоподобно (ср. с рис. 38 а): Но картина меняется, когда биомасса популяции достигает больших значений: здесь уже начинает сказываться от­рицательная обратная связь — «загрязнение» среды продуктами жизнедеятельности организмов, метаболита­ми Мг — И в зависимости от того, с какой скоростью от­водятся эти метаболиты, биомасса популяции выходит на определенный постоянный уровень (кривые ВЮ, 1), или, если они отводятся из среды недостаточно быстро (кривая 2), популйция начинает погибать. В лаборатор­ных опытах действительно приходится предпринимать специальные усилия, чтобы популяция не погибла. В природных же условиях среди миллионов видов орга­низмов, населяющих океан, на любой метаболит нахо­дится свой «мусорщик», для которого именно этот мета­болит оказывается лакомым кусочком. «Мусорщики» от­водят метаболиты из среды, усваивая их и тоже

начиная развиваться взрывоподобно, пока их собствен­ные продукты жизнедеятельности не начнут тормозить их развитие. Всегда находятся следующие и следующие «мусорщики», и таким образом прокатывается волна жизни. Водоросли выделяют органические ве­щества, которые потребляют бактерии-гетеротрофы, ми­нерализующие органическое вещество. Токсичный для них минеральный продукт их жизнедеятельности — ам­миак — используют нитрифицирующие бактерии, окис­ляя аммиак до нитритов, этот продукт подхватывается следующим видом микроорганизмов и окисляется до нитратов, а нитраты снова используются водорослями для синтеза аминокислот и белков, необходимых им для построения своего тела. Круг замыкается. Такое мирное сосуществование оказывается выгодным всем обитате­лям океана, ни одна популяция не погибает, ведя мир­ную «торговлю» метаболитами с соседями и поддержи­вая этим свою биомассу на определенном стационарном уровне— вся биологическая система оказывается нахо­дящейся в динамическом равновесии. Конечно, кроме этих факторов, действует и множество других, не менее — важных, например, отношения типа «хищник — жерт­ва», но и в этом случае устанавливаются определенные равновесные соотношения между .различными популя­циями. Океан оказывается огромным биостатом и одно­временно — хемостатом, так как потоки метаболитов — химических соединений — оказываются упорядоченны­ми, и благодаря этому концентрации этих химических компонентов морской воды стационарны.

Но и здесь случаются локальные метаболические войны, находятся нарушители мирного сосуществования популяций, и морская вода окрашивается, буквально, в кровавый цвет. «Red tide» — красный прилив —такой термин утвердился в океанологии за одним из явлений нарушения биохимического равновесия в океане, мест­ной «поломки» биостата, когда не вполне объяснимый пока взрыв популяции красных водорослей отравляет вокруг все живое. Однако агрессора усмиряют пока что довольно быстро; так как и его жизнь зависит от дру­гих, и местный биохимический конфликт не перерастает в’мировую"войну популяций.

Описание «красного прилива», продолжавшегося, по словам1 автора,- шесть месяцев, дано в статье Б. Лефев — ра «Океан в опасности»[31], откуда мы приведем выдерж­ки: «В ноябре 1946 года жители Форт-Майерса (штат Флорида) были поражены, увидев «красное море», на поверхность которого всплыло множество мертвой рыбы (от 100 до 150 кг на квадратный метр). Вначале поду­мали, что это последствия противозаконного сбрасыва­ния какого-то химического вещества. Однако в действи­тельности дело обстояло иначе.

На самом деле это было внезапное «нашествие» по — лурастительных, полуживотных организмов — динофла — геллятов, размножению которых способствовало нали­чие в прибрежных водах излишнего «корма». Эти микро­организмы, развитие которых стимулировалось избыт­ком кобальта и витамина В12 и которые жадно поглощали фосфор и азот, в изобилии содержавшиеся в отбросах, до такой степени расплодились, что даже окрасили море». . —

Затрагивая проблему сохранения окружающей нас среды, будем иметь в виду, что человечество становится все более существенной частью глобального биостата. Об этом говорит даже простой рост его численности, по­казанный на рис. 38 в[32]. Сравнивая последний рисунок с предыдущими (38 а, б), отметим неожиданное сходство: картина на рис. 38 в не отличима от начальных этапов развития популяции организмов, моделирование которой мы только что провели с помощью ЭВМ. Если сохра­нить использованные выше названия, то на кривой рос­та на рис. 38 в. также можно выделить лаг-фазу, соот­ветствующую адаптации, к условиям среды, и фазу экс­поненциального роста, начинающуюся в 18 веке. Как будет идти эта кривая дальше, зависит, помимо других обстоятельств, и от того, с какой эффективностью чело­вечеству удастся решить — проблему защиты окружаю­щей среды, распоряжения отходами своей многогран­ной жизнедеятельности. Влияние метаболитов челове­чества — продуктов его жизнедеятельности, прежде все­го надо говорить о промышленности, — на начальном участке экспоненциального роста не сказывалось замет­ным образом на среде обитания в целом, хотя локаль­ные нарушения равновесия в среде отмечались в исто­рии неоднократно. Наконец, сейчас мы находимся вбли­зи критической точки, когда метаболиты популяции за­метным образом влияют на среду или угрожают ей, и теперь от скорости отвода одних метаболитов и от воз­можности ограничения и запрета других, быть может, зависит, пойдет ли развитие популяции по кривой ВЮ и 1 (колебания вблизи оптимальных значений в пределах Земли) или по кривой 2 на рис. 38 б. Расхищение пище­вых и энергетических ресурсов может усугубить неже­лательное направление развития.

Важную роль в отводе метаболитов, как мы уже го­ворили, играют биологические «мусорщики», которые обязательно найдутся почти для любого вида отходов жизнедеятельности человека. Развитие новых популяций «мусорщиков» нуждается в контроле и регулировании, иначе оно может привести биостат в состояние такого равновесия, которое нежелательно для человека (вспом­ним «цветение» красных водорослей). Но для контроля и регулирования надо знать более точно, как устроен биостат, какие связи в нем существуют, насколько он устойчив, че‘м определяется его устойчивость.

Значит, мы должны усложнить нашу модель и рас­сматривать не одну популяцию, пусть и с учетом хими­ческих компонентов, в том числе метаболитов, а сово­купность популяций в их химическом и биологическом взаимодействии.

Комментарии запрещены.