Бурение грунтовых зондов, установка энергетических колодцев

Океан, как и клетка, является открытой систе­мой, открытой для обмена веществом и энергией с окру­жающей средой (для внешнего метаболизма), и следо­вательно, он должен обладать определенными свойства­ми, характерными для любых открытых систем, делающими их похожими друг на друга. Чтобы отчет­ливо представить себе особенность этих свойств,’ сравним динамику процесса в открытой и закрытой (для обмена веществ) системах. Для примера возьмем двуокись угле­рода, растворенную в морской воде. Пример закрытой системы — фотосинтез в закрытой склянке, в которой из живых организмов находятся только фотосинтезирую­щие водоросли. Если концентрация водорослей постоян­на, то скорость фотосинтеза, регистрируемая по убыли двуокиси углерода, прямо пропорциональна наличной концентрации С02, (сі):

(92)

Начальное условие с = с (0) при t — 0.

Значение интеграла можно найти в таблице интегра­лов. Получим.

(93)

с, ~сг(0)e-*ia<.

По виду уравнения (93) можно легко предсказать, что же произойдет с. СОг в закрытой системе. С увели­чением времени t экспонента, а значит и с і постепенно становятся все меньше. При достаточно большом вре­мени опыта, в крайнем’ случае при t, стремящемся к бес­конечности (f->оо), экспонента равна нулю, и следова­тельно, Сі = 0, . —

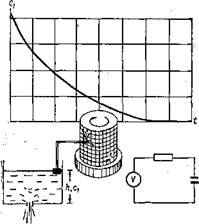
’ Можно не прибегать к интегрированию, чтобы полу­чить точную зависимость с от t, а воспользоваться. ка­кой-нибудь хорошо известной из практического опыта аналогией. Такой метод, называемый методом анало­гового моделирования, широко и эффективно исполь­зуется при изучении различных динамических систем. Например, опыт с «дырявой кастрюлей» (рис. 31) . Уро­вень воды h в такой кастрюле, аналогичный по матема­тическому смыслу концентрации а, понижается со вре­менем, по уравнению (92), тем быстрее, чем выше

Рис. 31. Гидродинамическая и t электрическая модели. реакции (92) в закрытой системе. .

уровень воды и чем больше величина отверстия, которая аналогична константе скорости kn. Такой метод, назы­ваемый гидродинамическим моделированием, успешно использовался до недавнего времени для самых серьез­ных и важных расчетов. Или же хорошо известное даже из школьного курса обстоятельство, что напряжение U в электрической ^С-цепи падает точно в соответствии с уравнением (92):

dU 1

■и,

dt

(920

напряжение U аналогично концентрации с, а величина 1/# аналогична константе скорости кц.

Этот метод благодаря быстроте электрических про­цессов и возможности простой, точной, надежной и на­глядной регистрации результатов на самописцах или ца цифропечатающих устройствах широко используется в настоящее время. Самописец, соединенный с потенцио­метром или с поплавком в «дырявой кастрюле», проин­тегрировав уравнение (92), начертит точно по уравне­нию (93) график зависимости концентрации СОг. от времени опыта в виде кривой, изображенной на рис. 31 (напомним, для закрытой системы). .

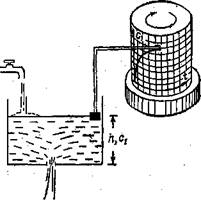
Рис. 32. Гидродинамическая модель реакции (94) в открытой системе.

Теперь легко можно промоделировать этот процесс для условий открытой системы. Подсоединим к «ды­рявой кастрюле» кран и приоткроем его (рис. 32). Очег видно, если мы достаточно’ открыли кран и дыра в ка­стрюле не слишком велика, несмотря на то, что часть воды из кастрюли выливается, в ней начнет прибывать вода. Но по мере того, как уровень воды будет повы­шаться, скорость оттока воды через дырку, пропорцио­нальная уровню воды, тоже будет возрастать. Наконец* наступит момент, когда скорость притока воды из крана и скорость оттока воды через дырку станут совершенно одинаковыми и уровень воды закрепится на одном, оп­ределенном месте, а именно на месте, определяемом ско­ростью потока из крана и величиной дыры в кастрюле;. Здесь существенны два обстоятельства. Первое: этот постоянный, стационарный, уровень может сохраняться неизменным как угодно долго, пока не изменится поток из крана. Второе: получим совершенно тот же. по вели­чине стационарный уровень, если в любой момент вре­мени— в самом начале, как только открыли кран, в се­редине или в конце, когда установился стационарный уровень, — плеснем в кастрюлю дополнительную порцию воды, причем как угодно большую, пусть даже кастрюля наполнится до краев. Если при этом уровень воды пре­высит тот самый предопределенный притоком из крана и дырой (т. е. кинетическими параметрами) стационар— ный уровень, то при такой высоте уровня воды в ка­стрюле напор будет велик, и скорость истечения воды через дыру превысит скорость притока воды из крана—• уровень начнет понижаться и до тех пор, пока не займет свое предопределенное положение. Такое свойство от­крытых систем — предопределенность стационарного со­стояния кинетическими параметрами и независимость его от состояния системы в достационарное время — назы­вается эквифинальностью. Аналогично этому будет и по­ведение нашей открытой химической системы, динамику которой мы уже промоделировали, имея в виду, что из­менение уровня воды в кастрюле аналогично изменению концентрации вещества в морской воде, приток из кр. а-’ на — поступлению вещества в океан, а отток через дыр­ку— исчезновению вещества из морской воды.

Оставим, однако, аналоговые модели для более слож­ных задач, тех, аналитическое — решение которых (т. е. точное математическое решение в виде формул) полу­чить очень трудно либо вообще невозможно. Пока слож­ность задачи позволяет получить формулу, даже прибли­женную, ее стоит получить, потому что аналитическое ре­шение обладает определенным достоинством, .которого не знает даже мощнейшая ЭВМ, а именно — общностью, тем, что исследователь не связан с конкретными циф­рами и параметрами. Начнем анализ открытой системы опять с растворенной СОг, потом попытаемся обобщить результат. Предельно упростим задачу, пренебрежем для этого обратным потоком k2 и остальной частью карбо­натной системы. В левой части уравнения запишем то, что наС интересует: скорость изменения концентрации С О 2,01: :dci/dt. В правой части сведем. баларс: мы должны при наших упрощениях учесть обмен С02 с атмосферой и по-

требление СОг на фотосинтез. Таким образом, учиты­ваем в приходной части: 1) скорость образования СОг в системе равна нулю ri, (+) = 0; 2) скорость поступления С02 из атмосферы ®ь (+) пропорциональна ее раство­римости Yi при данных условиях и ее концентрации с’ в атмосфере w, (+) = аіуіс/; в расходной части: 1) ско­рость расходования СОг на фотосинтез, как-уже делали, примем равной гь (_) = йігСь 2) выделение С02 в атмо­сферу СО СКОРОСТЬЮ W, (_) = 61С1. •

Теперь запишем балансовое уравнение, приведя его к виду, удобному для обобщения:

■ dCd =П, (+> + «’1, (+) — П, (-> — п>1, (-) =

= Otjf jCj ^1^1 ==: alT 1^1 (^12 ^l) (94)

Если бы мы хотели учесть еще какие-либо статьи ба­ланса, мы аналогично добавили бы в правую часть соот­ветствующие слагаемые. Уравнение (94) можно, решить очень легкй, если считать величину с постоянной.

Интегрируя уравнение (94) при начальном условии Сі = Сі(0) — при t = 0, получим:

„ “iVi {„ кл “iTici

с^-^г)^+К) С95)

В отличие от закрытой системы, как это и предсказано гидродинамической моделью, здесь при достаточно боль­шом времени t-*~°о, когда экспоненциальный член ста­новится равным нулю, значение сі перестает понижаться и действительно достигает предела (обозначим его Сі):

— а,-‘ с, .

Сх~ ^12 + 5! ’ . ■ (96)

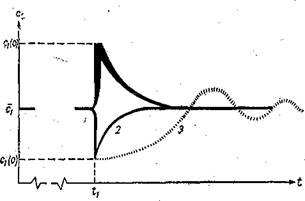
Т. е. СО временем В открытой системе концентрация Cl достигает стационарного значения а, причем это зна­чениеСі не зависит от самой наличной концентрации С02 в морской воде, а определяется концентрацией ее в атмо­сфере (с,) и кинетическими параметрами (эквифиналь — ность). Предположим, что внезапно произошло возму­щение в момент временн ой разовое увеличение концен­трации С02, например, из-за вулканического выброса в океане (кривая 1 на рис. 33) или’уменьшение сь на­пример, из-за резкой интенсификации фотосинтеза (кри­вая 2 на рис. 33). Тогда, согласно уравнению (95), кон­центрация СОг (сі) постепенно автоматически вырав­няется до прежнего стационарного уровня с і сверху (кривая 1) или снизу (кривая 2) соответственно, неза­висимо от того, до таких значений произошло первона­чальное изменение концентрации ССЬ; ее стационарное значение соответственно принципу эквифинальности пре­допределено кинетическими параметрами.-

Рис. 33. Переходный процесс в открытой динамической системе первого — кривые (/), (2) и более высокого — кривая (3) порядка после возмущения в момент вре-. мени t, в результате которого произошло повыше — ниє (1) или понижение (2) концентрации Сі от стацио­нарной cj до Сі (0).

Легко заметить, что временные переходные характе­ристики, представляемые этими кривыми на рис. 33, ана­логичны пространственным переходным характеристи­кам на рис. 30. Суть аналогии ясна — и в том и в другом случае речь идет о переходе соответственно. во времени и; в пространстве от возмущенного состояния к стацио­нарному, эквифинальному. Оба рисунка совместно дают представление — о пространственно-динамической струк­туре океана, о саморегулировании в нем и о причинах его устойчивости.

Из уравнения (94) стационарное значение с легко получить без всякого интегриррвания, просто из условия

стационарности. Перепишем, учитывая условие стацио­нарности (dci/dt = 0), уравнение (94), отметив черточ­кой стационарные с. Получим алгебраическое уравне­ние — . ‘

aihc’i — (£12 + 8i) £1 = 0, (94′)

W ^12 +

(960

решим его

Выражения (960 и (96) полностью совпадают.

Используя этот простой способ, покажем, что вся си­стема в целом, со всеми ее химическими компонентами, аквифинальна и что океан, следовательно, подобно живой клетке, стремится в ответ на возмущение вернуться в определенное природными условиями стационарное со­стояние. Не будем при этом ограничиваться какими-то определенными химическими компонентами и определен­ными видами обмена веществ.— это может быть и реч­ной сток, и обмен с атмосферой, и обмен с дном.

Для п компонентов этой системы, в том числе для изображенных на рис. 29, аналогично выше описанному может быть выписано п линейно независимых дифферен­циальных уравнений, совокупность которых полностью описывает динамику системы: ~

~^Г~ = П, (+) — п, (_) + Wi’ (+) — wt, <-) = •

— = а(Т/с« ~Ь w‘, <+) — {ki, і++ A) ci

.. (г= 1, 2, ..я), (97)

где Гр (+), гц-)— скорости соответственно образования и расходования г’-того компонента; Сі, с/ — концентрации компонентов соответственно в системе и вне ее, откуда этот компонент поступает в систему; аг-, уи Si— коэффи­циенты, вид которых зависит от того, каким образом реализуется обмен веществ с окружающей средой.(не­которые из них могут быть равными нулю или еди­нице). — • — …

Из общей совокупности, уравнений (97) можно опре­делить все стационарные концентрации с,-, пренебрегая
для этого производными dci/dt, как в (94′), и решая полученную таким образом систему алгебраических уравнений:

Г1> ( + ) (С1> СЪ ■ • •> Сп) ~ г1, (—) (с1> ^2) • • •> сл) ~Ь ( + ) (^li ^2і • • •> £„• ^2, . • •, Сл)

— «»,,(_) (с J, С2, С„, сі, 4 .Сл)=0

. ‘ (/=1, 2………. я). (98)

Так как уравнение (98) не содержит начальных и теку­щих концентраций Сг(0), а, то определяемые из урав­нения (98) стационарные концентраций а никак не за­висят от начальных с,(0) и вообще от концентраций ком­понентов в любой момент времени. Таким образом, для всей системы в целом выполняется принцип эквифиналь — ности.

Но трудно предполагать, чтобы приток веществ в океан всегда был постоянным. Другими словами, в на­шей гидродинамической модели (см. рис. 32) кран, ско­рее всего, пульсирует. Если интервалы между пульса­циями гораздо больше, чем время «ответа» системы — время ее возвращения в прежнее состояние, то такие возмущения никак не скажутся на состоянии системы, даже если приток из крана соизмерим с количеством воды в кастрюле. В случае же океана приток ничтожен по сравнению с его массой, и даже частые «пульсации» не скажутся на его химическом облике.

Читатель мог бы промоделировать реакцию системы, скажем, на экспоненциально растущее возмущение — за­грязнение океана.

Если из рис. 29 для упрощения изолировать элемен­ты с/, Сі, Сі от остальной части системы и рассматривать как прямой (km), так и обратный (&2i) потоки, то при термодинамически устойчивом равновесии должно быть

с2 ^12 TS

Cl ~ *21 ~А’

где К — константа равновесия. Аналогично предыду­щему, из уравнений (97) легко-показать, что соотноше­ние стационарных концентраций СОг, ок и растворенного

где. . . .

органического вещества (РОВ) определяется выраже­нием

■ Л = 8А/(аіїіС1 + а2Ї2С2),

т. е. отношение стационарных концентраций сг/сі-не рав­но константе’ равновесия К = &12/&21, как это должно быть при условии термодинамического равновесия. Эти выводы можно распространить и на всю систему цели­ком, т. е., несмотря на протекающие процессы трансфор­маций соединений углерода, в системе как угодно долго могут поддерживаться термодинамически неравновесные концентрации веществ. Океан, таким образом, как и клетка, как и любой живой организм, является «хемо­статом», термодинамически неравновесной системой, со­храняющейся в стационарном состоянии благодаря об­мену веществ с окружающей средой; это термодйнами — чёски неравновесное стационарное состояние и есть его «жизнь». Напрашивается вопрос: нельзя ли рассчитать, как долго будет сохраняться это состояние стационар­ности. Клетке удается сохранять его сутками и годами, организму — десятками и сотнями лет. А океану? Можно ли рассчитать предопределенное параметрами системы (как и в случае клетки, организма) время жизни океа­на? Пока не известно.

Обычно химики, когда нет ни теоретической, ни экс­периментальной опоры, апеллируют к массам элементов системы. Последуем этому пути: масса клетки 1 • 10-18— — 1-Ю-20 кг, время жизни сутки X fi] масса организма /г-10-1 — /г-102 кг, время жизни п — /г-102 лет; масса океана 2 • 1021 кг, «время жизни» больше 1010 лет. «Про­жито» 3 — 5 • 109 лет. Так что океан еще пока молодой организм в расцвете сил?

Конечно, приведенные выражения и рисунки до чрез­вычайности упрощают картину, хотя и передают основ­ной смысл и тенденцию. Стационарные концентрации, конечно же, не достигаются плавным монотонным изме­нением, аналогичным кривым 1 и 2 на рис. 33 (здесь,, преднамеренно упрощая картину, представляем рассмат-

риваемую систему как динамическую систему первого порядка). В действительности же ее порядок заведомо выше первого. Кривая 3 на рис. 33 отражает реакцию более сложной системы на то же самое возмущение. Как мы видим, в этом случае переходный процесс от возму­щенного состояния к стационарному может носить иной характер, например может оказаться колебательным. Однако для нас сейчас существенно лишь то, что в этом случае, при затухающих колебаниях, принцип эквифи — нальности не нарушается, а при колебаниях незатухаю­щих действует принцип сохранения средних значений — система устойчива.

Наивно было бы полагать, что замечательная устой­чивость «параметров» океана обеспечивается только этими принципами. В действительности, кроме этих мощ­ных, но грубых механизмов регулирования, на каждом уровне системы функционируют специальные механизмы тонкой регулировки, причем обычно обеспечивается мно­гократная и разнообразная подстраховка — залог на­дежности работы всей системы. Эту автоматику с под­страховкой можно увидеть, проследив за ионами Н+.

Комментарии запрещены.