Планетарный вихрь и движение вод
Планетарный вихрь и движение вод
— На поверхности воды трудно представить холмы или впадины. Если прекратятся усилия, которыми поддерживаются неровности водного рельеф, а (например,, центробежное ускорение), то поверхность будет — быстро — выравниваться токами воды. Однако эти представления оказываются несостоятельными, если перенести их из — лаборатории на морскую’ .поверхность большой протяженности. Допустим, что морская поверхность по — нижаетюя к центру какого-нибудь района. Наклон поверхности — вызовет градиент давления, который будет стремиться переместить воду и заполнить понижение..
Если плотность воды однородна, величина градиента давления зависит только от наклона поверхности у и выражается формулой
= =g tg т. (7)
вде а — плотность воды; g — ускорение свободного падения. Под действием градиентной силы единичный объем воды будет приобретать секунда за секундой все большую скорость, и если бы не было помех, впадина быстро заполнилась бы водой.
Однако, благодаря суточному вращению Земли, на* (всякое тело, движущееся по земной поверхности, действует поворотная кориолнсова, или геострофическая*, сила. Эта сила направлена перпендикулярно движению— вправо в северном полушарии и влево в южном. В. нашем полушария она вызывает подмыв правых ‘берегов рек и ускоряет износ правых колес поездов. Ее величина пропорциональна скорости движения относительно земной, поверхности и синусу географической широты местам. .
— Fa = т 2со sin ср = истО, (8)
где © — угловая скорость вращения Земли; ф — географическая широта места; и — вектор скорости течения; S —планетарный івихрь.
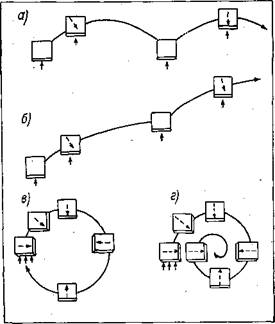
Действие поворотной силы приводит к тому, что ‘траектория частицы воды будет не прямолинейной, а •примет форму петли, показанную на рис. 2 а. В вершинах петель частица движется перпендикулярно к наклону уровня и вызванной наклоном градиентной «силе Fr. Продолжая петлеобразное движение по циклоиде, частица воды (если ее движению не мешает трение) будет уходить все дальше в направлении, перпендикулярном наклону уровня, не изменяя своего среднего положения ни вверх, ни вниз по наклону. Если мы ©мешаемся в процесс движения и заставим наклон уровня увеличиваться во времени, то среднее положение частиц начнет смещаться вниз, противодействуя увеличению найлона. Если мы начнем уменьшать наклон, то среднее положение частиц станет сдвигаться
вверх, против наклона, и будет препятствовать его уменьшению. .Конечно, такие вмешательства или опыты можно осуществлять только «а математических моделях движения.
Присутствующее во всяком движении поворотное ускорение Земли стремится стабилизировать неровно-
|
Рис. 2. .Влияние силы Кориолиса на траекторию. частицы (по Р. Стюарту, 1969). |
Пунктирные стрелки показывают направление силы Кориолиса; одиночные стрелки — направление постоянной движущей силы; тройные стрелки — направление кратковременного толчка.
сти уравенной поверхности океана. Этот эффект нельзя наблюдать в лабораториях, а тем более предвидеть из ‘повседневного опыта, поскольку размеры петель, опи — сьюаемых частицами воды, выражаются /в километрах.
В табл. 1 приведены размеры петель: их ширина L в направлении, перпендикулярном к действующей силе,
|
Параметры колебательных движений при действии постоянной силы 10~3 дин
|
глубина D в направлении действующей силы, максимальная скорость в направлении. силы Ux и поперек нее Uv, а кроме того, время движения вдоль одной петли Т для разной географической широты ср и при постоянной действующей на воду силе, равной 10~3 дин. Это такая шла, которая соответствует градиенту давления при возвышении уровня моря в 2 мм на расстоянии 1 мили (18.52 м).
При, использовании таблицы надо иметь в виду, что скорость движения, и размеры петель зависят от величины силы линейно, поэтому при изменении силы в ^произвольное число от раз нужно величины L, D, Ux, Uу умножить на т. В то же время величина Т при изменении силы меняться не будет.’
На рис. 2 в дополнение, к петлеобразным движениям чводы, которые возникают при действии на частицы, постоянной силы, приведены траектории инерционного. движения, — которое длится после прекращения действия движущей силы. При отсутствии трения (рис. 2 в) это..движение идет по кругу инерции. Радиус круга инерции ..зависит от скорости течения и географической широты места. При скорости 100 см/с на широте 40° радиус «будет равен 10 км. Оплошные стрелки на рисунке обозначают движущую силу течения, а пунктирные стрелки —поворотную.
Может показаться странным,’ что мы говорили о движении морских’ вод, не принимая во внимание
силу трения. В повседневном опыте эта сила всегда сопровождает движение воды, но в океане во многих случаях можно ею пренебрегать. Дело в том, что сила трения возникает за счет разности скоростей соседних слоев жидкости. Такая разность обычно проявляется, благодаря тому, что на границах потока жидкость как. бы прилипает ко дну и стенкам. Прилипание существует и в океане, однако там расстояния до границ потока. могут быть очень значительны, а разность скоростей мала. Возможность не учитывать силу трения в потоках, не вызванных ветром, и удаленных от дна, подтверждают проверки, сделанные и прямым измерением скоростей, и расчетами. Если же силу трения ввести в вычисления траекторий частиц, что необходимо, например, на мелководье, то получим движения, показанные на рис. 2 б и 2 г.
|
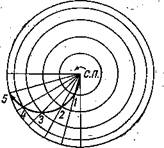
Рис. 3. Искривление прямолинейной траектории засчет — вращения Земли. |
Чтобы понять происхождение .поворотной силы, проделаем мысленный опыт. На рис. 3 показана проекция земных меридианов и параллелей на плоскость, касательную к земной поверхности в точке Северного полюса. Если пустить из точки полюса вдоль меридиана какое-то тело, не связанное трением с земной поверхностью, то под действием, начального толчка это — тело станет скользить по поверхности, сохраняя направление своего движения в перпендикулярной чертежу — плоскости начального меридиана.
’ В то. же время поверхность Земли, не связанная трением с движущимся телом, будет равномерно вращаться под ним со скоростью.360° за 24 ч, или 1440 мин, и; поэтому через каждые 4 мин (1440 мин: 360°) под телом іпройдет, новый меридиан, допустим 1° з. д., 2° з. д.. и т. д. .
Таким’ образом, движение тела будет отклоняться от земных ориентиров вправо. Двигаясь по инерции, тело.(допустим, ракета) через равные интервалы времени^попадает в точки земной поверхности, показанные на рисунке;
цифрами 1, 2, 3, 4, 5. Расстояния между параллелями, на гкоторых лежат точки, — неодинаковы ввиду того, что движение по инерции прямолинейно, а земная поверхность лскривлена.
Очевидно, что как бы мы ни увеличили, массу раже™, три неизменной, скорости движения к югу ракета лройдет над одними и теми же пунктами земной поверхности. Действие силы Кориолиса останется неиэ — менным, а значит, величина силы ‘возрастет, во столько. же раз, ©о сколько возросла масса тела. Таким обра — .зом, так же как и сила тяжести, сила Кориолиса относится к массовым силам. Однако если для силы тяжести мы можем назвать взаимодействующие тела, причем с массами, ‘пропорциональными величине взаимодействия, то сила КориоЛиса, как видно из нашего примера, возникает без взаимодействия с каким-либо телом, иными словами «неизвестно откуда». За это не-‘ «подчинение третьему закону Ньютона силу. Кориолиса относят к числу сил фиктивных. —
(Внимательный читатель, возможно, вспомнил круг :инерции, показанный «а рис. 2 в, и удивился, что ракета не возвратилась в точку запуска по этому кругу. Прилгана здесь та, что. круг инерции справедлив для случая, когда величина поворотного ускорения останется в процессе движения постоянной. Это должно быть, если сеографическая широта не изменилась. Такой случай, конечно, до некоторой степени условен, «о при. радиусе ■круга 10 км изменения широты так незначительны, что «почти не влияют на траекторию. Движения, близкие — к кругам инерции, но менее правильные, удавалось наблюдать в океане. .
Наконец, может возникнуть и такой вопрос: почему шланетарный вихрь уменьшается к — экватору, если угловая- скорость вращения планеты одинакова для всех ее •точек? Причина в том, что течение отклоняет не вся угловая скорость, а лишь ее проекция на перпендикуляр к, площадке, касательной к земной поверхности тз данной точке. Величина проекции равна ©sirup. Именно с такой угловой скоростью площадка поворачивается вокруг своего центра в процессе суточного вращения Земли (вспомните опыты с маятником Фуко). Значит, эффективность влияния силы Кориолиса на движение воздуха и воды меняется на Земле в очень
широких пределах. Поскольку на экваторе эта сила равна нулю, частица, направленная от экватора к полюсу, может пройти значительное расстояние, прежде чем она будет повернута на восток. Примером тому служит антипассат в атмосфере (ом. рис. 13). .