Бурение грунтовых зондов, установка энергетических колодцев

Солнце почти одинаково нагревает оба полуша­рия. Приход его радиации зависит от географической широты. Но одинаковый приток тепла дает различные результаты. В северном полушарии вблизи параллели 55° расположены плодородные берега Англии, Дании, леса Подмосковья, а на той же широте южного полуша­рия, на меридиане Парижа, лежит остров Буве, погре­бенный под толщей вечного льда.

На два полушария можно смотреть как на две при­родные модели планеты и, сравнивая их, оценивать зна­чение особенностей географической оболочки для тепло­вого равновесия земной поверхности. Но сравнительное описание дает лишь качественные ответы. Например, на карте мира видно, что остров Буве лежит в центре океа­нического кольца, огибающего планету в широтном на­правлении, и что к югу от этого кольца расположен об­ширный ледяной материк. ‘

Поиски количественных связей, а также ответов на вопрос о причинах, вызывающих ту или иную обстанов­ку (например, Антарктида — эт. о результат или причи­на холодного климата), требуют создания математичес­ких моделей. Такие модели схематизируют изучаемые объекты, выделяя в них главные связи и зависимости. Рассмотрим это сначала на самой простой модели.

Предположим, что тепло поступает к земной поверх­ности только за счет радиации Солнца, а уходит от по­верхности только за счет излучения в космическое про­странство. Обозначим приход тепла Q, а расход — 1. Если Q>/, то поверхность Земли нагревается, если Q<V — охлаждается. Будем искать температуру равно­весия, когда Q — /. Из учебников физики нам известен закон теплового излучения:

i = sXW, ‘ (71)

где і — величина излучения с единицы поверхности; 0 — абсолютная температура поверхности (температура в градусах Кельвина); % — коэффициент, постоянный для всех поверхностей и температур (постоянная Стефана — Больцмана); s — коэффициент, характеризующий инди­видуальные особенности поверхности.

Умножив выражение (71) на площадь Земли, най­дем величину ее теплового излучения: —

/ = 5Х64- 4«Яа, (72)

где R —г радиус Земли.

Суммарное поглощение солнечной радиации поверх­ностью планеты запишем формулой

, Q = q(-a)«H V (73)

где q ■— радиация, падающая на единичную площадку, расположенную перпендикулярно к лучам Солнца;

а — та часть радиации q, которая отражается планетой в космическое пространство; nR2 — площадь сечения Земли.

Приравняем выражения (72) и (73) и вынесем тем­пературу в левую часть формулы;

4/ -irVtTb. (74)-

— Как известно из наблюдений, средняя температура земной поверхности в современную эпоху примерно 15°С, или 288К. Среднее значение коэффициента а 0,32. Из этих данных найдем значение первого корня в правой

Современная температура

v 0,2 0,4 0,6 о, a« Альбедо поверхности Земли

Рис. 16. Зависимость средней температуры поверхности Зем­ли от ее альбедо.

части формулы (74):

4s X

: 317,1 К. (75)

Предположим, что эта величина остается постоян­ной. Тогда можно построить количественную связь меж­ду температурой. поверхнос­ти и коэффициентом а. Этот коэффициент—альбедо по­верхности (albedo — белиз­на). Он имеет максималь­ное значение для снежно­ледяной поверхности (а^ = 0,8) и минимальное для — водной (а = 0,1). На рис. 16

мы построили график, показывающий связь между сред-, ней температурой поверхности Земли (в °С) и ее альбе­до. График вычислен по формуле

(76)

= 317,1 V (1 — а) -273.

Из рисунка видно, что планеты, получающие одина­ковое тепло от своих солнц, могут иметь большие разли­чия температур в зависимости от характера своей по­верхности. В нашем примере это различие меняется в диапазоне почти 100° С. Конечно, построенная модель (ее идея заимствована из работ М. И. Будыко) очень приблизительна. Она грубо учитывает влияние атмосфе-

ры на тепловое излучение (с помощью постоянно­го коэффициента s) и не разделяет суммарное от­ражение радиации в космическое пространство (ко­эффициент а) на Отражение от облаков и от земной по­верхности. —

По такому же принципу, как была построена модель, т. е. из~ условия теплового равновесия, можно рассчи­тать, как изменится температура какого-то района Зем­ли при появлении или исчезновении на нем ледяного по­крова. Эти расчеты должны, однако, учитывать новое обстоятельство — перенос тепла воздушными и морски­ми течениями.. Особое значение имеет при этом перенос меридионального направления. Остров Буве расположен в центре огромного течения, расход воды в котором в 7 раз больше, чем у Гольфстрима. Однако течение Южно­го океана огибает Землю вдоль параллелей, и это огра­ничивает его влияние на климат. Но верхние слои воды под действием ветра все-таки медленно смещаются к се­веру, неся с собой холод и льды от антарктического по­бережья. .

Приведем несколько цифр, показывающих роль океа­нических течений в формировании климата. Объемная теплоемкость воды примерно в 3200 раз больше, чем воздуха. Это значит, что 1 м3 воды, охлаждаясь на Г, может нагреть на Г столб воздуха сечением 1 м2 и вы­сотой более 3 км. Но 50% всего воздуха атмосферы сосредоточено в ее нижнем пятикилоцетровом слое. По­этому теплоемкость всей земной атмбеферы равна теп­лоемкости трех верхних метров океана. Еще более вну­шительны величины тепла, выделяющегося при замерза­нии и испарении воды. При замерзании одного объема воды от. нее отнимается тепло, достаточное для нагрева­ния на 1° 250 000 объемов воздуха, а при испарении — 1 800 000 объемов.

Перечисленные свойства воды приводят к тому, что океан реагирует на изменения солнечной радиации, в том числе на ее годовой ход, совсем иначе, чем твердая суша. Поглощая или отдавая большое количество теп­ловой энергии, он мало изменяет свою температуру.

Физиологическое ощущение холода различно при со­прикосновении со сталью и деревом одинаково низкой температуры. Причина заключается в том, что на месте соприкосновения двух тел (например, палец—‘дерево)

мгновений устанавливается температура Ьт, которая де­лит разность между начальными температурами поверх­ностей (йд — ‘Од) на два отрезка, отношение между ко­торыми обратно пропорционально коэффициентам теп — лоусвоения тел: .

Коэффициенты теплоусвоения определяются форму­лой

ь = уТак = са УК, (78)

где с — удельная теплоемкость вещества; а — его плот­ность; Я — коэффициент теплопроводности; К — коэф­фициент температуропроводности.

Коэффициент теплоусвоения, как видно из отно­шения (77), определяет способность тела противиться изменениям температуры на его поверхности. По форму­ле (78) можно подсчитать, что коэффициенты теплоус­воения меди, железа, песчаника и дерева относятся как 114:47:6:1. Труднее получить коэффициенты тепло — уовоения для воды и воздуха. Опыт нам подсказывает, что ощущение человеком температуры этих сред зависит от их подвижности. Происходит так потому, что вместо молекулярной температуропроводности в движущейся среде нужно учитывать турбулентную температуропро­водность, связанную с вихревым перемешиванием. Эта температуропроводность в десятки тысяч раз больше мо­лекулярной. Так, коэффициент молекулярной температу­ропроводности воды 1,4 -10-3 см2/с, а турбулентной — ме­няется в зависимости от скорости течений в пределах от 1 до 100 см2/с. При /С= 1; 10; 100 коэффициент тепло­усвоения у воды будет больше, чем у песчаника, соот­ветственно в 22; 70 и 220 раз.

,. До сих пор мы говорили о тепловом взаимодействии двух тел. Но одно из тел мы можем заменить эквива­лентным в каждый момент времени потоком тепла, на­пример потоком лучистой энергии. Реакция океана, су­ши и атмосферы на колебания этого потока и стала предметом исследования Такахаси.[18] Его модель включа­ет два уравнения. Первое выражает изменения тепло­содержания столба атмосферы, имеющего единичное се­чение:

= *($,-»), (79)

где С — теплоемкость столба; Ф — температура воздуха; 0s —■ температура поверхности; t — время; х — коэффи — цйент, учитывающий все виды теплообмена воздуха с подстилающей поверхностью.

Согласно уравнению (79), атмосфера прозрачна для солнечных лучей и нагревается только снизу от поверх­ности планеты, что почти соответствует действительно­сти. Изменение температуры воды или грунта определя­ется уравнением температуропроводности:

= (80)

Так же как и рассмотренные раньше уравнения дви­жения, уравнение (80) выражает баланс некоторой суб­станции. Баланс составлен для неподвижного кубика, вырезанного в пространстве воды или грунта. Левая часть уравнения обозначает скорость изменения тепло­вой энергии внутри кубика, деленной на теплоемкость и плотность вещества (эти величины сокращены в левой и правой части). Правая часть — разность между пото­ками тепла, вызванными теплопроводностью среды и пе­ресекающими нижнюю и верхнюю грани кубика. Вспом­ним, что похожим образом мы выражали результирую­щее воздействие на две грани кубика силы трения.

К двум уравнениям (79) и (80) добавляется гранич­ное условие, показывающее, чему равен тепловой поток Ф через поверхность моря или грунта:

‘ ■® = Q-/-x(»,-ft)t (81)

где Q — солнечная радиация, поглощаемая поверхно­стью; I — тепловое излучение поверхности, уходящее в космическое пространство.

Такахаси исследовал поведение модели при измене­ниях поглощенной радиации, заданных формулой

A Q = 0,01 Q0 cos tot, (82)

где Qo — среднегодовое значение радиации; со — частота

колебаний от очень быстрых, соответствующих суткам, до очень медленных, соответствующих тысячелетиям.

‘ —- 1—— І і і а- Ю 5 10 * 10’3 10~2 юш рад/год

В результате расчетов была получена связь между частотой колебаний радиации и амплитудой колебаний температуры океана. Эта связь имеет вид, близкий к кривой на рис. 17. Из рисунка следует, что чем меньше частота колебаний (т. е. длиннее их период), тем боль­ше изменение температуры. При нулевой частоте, ины­ми словами, при увеличении радиации на постоянную ве-

Рис. 17. Связь между час­тотой колебаний радиации и амплитудой ‘ колебаний температуры океана (по К.

Такахаси, 1965).

личину’ 0,01 Qo, температура поверхности океана изме­нится на 3,3° С, а при частоте, соответствующей годово­му периоду колебаний, — на 0,2°С.

Отсюда находим дополнительное объяснение суро­вости природы о. Буве — окружающий его океан не ус­певает за летнее время нагреваться настолько, чтобы растаял лед, покрывающий остров. Как подтверждают наблюдения, средняя величина сезонных колебаний тем­пературы на поверхности океана —около 2°, а на по­верхности суши— 20° С.

Советский геофизик С. Я — Сергин подошел к резуль­татам Такахаси с позиций теории управления. Он обра­тил внимание на то, что кривая на рис. 17 приблизи­тельно соответствует уравнению ~

‘ л(.)=т|а=. га

где Л(ю)’—ослабление амплитуды колебаний на выходе звена (температура) при увеличении частоты колеба­ний со на входе (радиация); А (0) —соотношение между амплитудами колебаний на выходе и входе при со = 0; Т — постоянная времени, характеризующая инерцион­ные свойства звена.

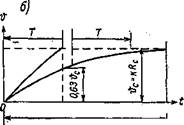
. Формула (83) относится к инерционному звену пер­вого порядка. Переходной процесс такого звена показан

на рис. 18. Из рисунка видно, что длительность пере­ходного процесса примерно равна утроенному значению постоянной времени, Сама же постоянная определяется как величина проекции касательной на линию установив­шегося значения новой температуры Фс-

Постоянную времени Мирового океана С. Я. Сергин получил по данным графика рис. 17 и формулы (83). Постоянная оказалась равной 2 тысячам лет с возмож-

‘

Яе

Рис. 18. Переходный процесс инерционного звена первого по­’ ■ рядка. ‘

tc *зТ

а — изменение во времени радиа — дии Я; б — изменение во времени температуры •&. " установившее­

ся новое значение температуры (входная характеристика звена);

/?с — установившеёся новое значе — * ние радиации (входная характерне- С тика звена; ^ — продолжитель­ность переходного процесса; Г— постоянная времени звена.

ным отклонением до 4 тысяч лет. Таким образом, про­должительность переходного процесса изменения тем­пературы океана имеет порядок 10 тысяч лет. Эта про­должительность не зависит от величины, на которую изменяется поступление радиации.

В один из периодов геологической истории океана значительная часть его воды перешла путем испаре­ния и осадков в континентальные ледяные щиты. Со­временные ледяные щиты Антарктиды и Гренландии зна­чительно меньше тех, которые были при максимальном развитии оледенений, но и они хранят такое количест­во льда, которое при таянии способно повысить уро­вень Мирового океана на 65 м и затопить приморские, наиболее населенные районы суши. Если мы вспомним затраты тепла на таяние льдов, то поймем, что процесс разрушения щитов очень длителен. Например, на него не хватило бы запасов тепла всего современного
океана. Ледяные щиты аккумулируют не только влагу, но и огромные запасы холода, а потому их надо считать вторым инерционным звеном в системе теплового вза­имодействия океана, суши и атмосферы;

В 1955 г. американским геологом В. Стоксом была высказана гипотеза, что взаимодействие двух инерци­онных звеньев — Мирового океана и ледяных щитов — должно иметь очень важные климатические следствия. Если система с такими звеньями будет выведена из со­стояния температурного равновесия с поступающим теп­лом Солнца, то она войдет в режим долгопериодных температурных колебаний, когда холодные ледниковые эпохи будут чередоваться с теплыми межледниковыми.

Физические причины таких колебаний были описа­ны Стоксом в статье «Новый взгляд на ледниковый пе­риод».1 Гипотеза Стокса, хотя и в качественной форме, объясняла то удивительное обстоятельство, что с нача­ла ледникового, или четвертичного, периода Земли (500 тысяч лет назад) оледенения проходили волнами, чередовавшимися с теплыми межледниковыми време­нами. Во время Последнего межледниковья (100 — 70 тысяч лет назад) на Восточно-Европейской равнине и средней Волге произрастали, вечнозеленые деревья, включая тисс, а дуб выходил за Полярный круг. Мак­симум же последней ледниковой волны наступил 20 ты­сяч лет назад. Это было время мамонтов, когда сред­неиюльские температуры в Европе упали ниже 6° С. До начала четвертичного периода средняя температу­ра океана была значительно выше современной (по Стоксу — на 10°). Следствием высокой температуры было большое испарение, влагосодержание воздуха и осадки. Какой-то первоначальный толчок, например повышение суши в районе полюса, нарушил равнове­сие влагооборота. Осадки, выпадающие На повышен­ную поверхность суши, не таяли, а создавали ледники. Альбедо поверхности повышалось и вызывало охлаж­дение.’ Падение температуры вело к уменьшению влаж­ности и осадков. Таким образом, между испарением и ростом ледников существовала отрицательная обрат­ная связь, которая могла бы ограничить рост ледни-

‘Stokes W. L. Another look at the ice age. — «Science», 1955, vol 122, N 3174, p. 815—821,

ков. Однако огромная температурная инерция океана эффективно препятствовала процессу охлаждения. Это достигалось перемешиванием охлаждавшихся поверх­ностных вод с глубинными, в то время теплыми во­дами. ,

Таким образом, оледенение смогло развиться в пол­ную силу и ледники вышли на берега океана. В даль­нейшем, в связи с понижением температуры и влаж­ности, скорость роста щитов за счет осадков стала уступать скорости их разрушения за счет таяния и отко­ла айсбергов. Ледники начали сокращаться, и созда­лись условия для возвращения океана к нормальной для него высокой температуре. Если бы не температур­ная инерция океана, то произошло бы быстрое — нагре­вание его вод, а возросшая при этом влажность и осад­ки остановили бы разрушение ледников. Но однажды охладившийся океан нуждается в тысячелетиях накоп­ления тепла, чтобы вернуться к прежней температуре. К этому времени ледяные щиты успевают частично или полностью разрушиться. Наступает теплый межледни­ковый период, за которым следует очередная волна оледенения.

Те же процессы взаимодействия были рассмотрены в 1966 г. С. Я. Сергиным, но в более полной, а главное, количественной форме.[19] Обратимся к схеме взаимодей­ствия, предложенной Сергиным (рис. 19). По этой схе­ме земная поверхность и атмосфера образуют систему, управляемую солнечной энергией.

Внешнее воздействие на систему — радиация Солнца. ‘ Она проходит сквозь атмосферу и трансформируется в тепло на поверхности планеты. Результатом этого воз­действия будет изменение средней температуры поверх­ности и изменение температурных градиентов. Последнее обстоятельство не учитывалось Стоксом, однако, по расчетам Сергина, оно имеет принципиальное значение для поведения системы и может переводить ее из области затухающих колебаний в область автоколебаний.

Чем вызван этот градиент и какие он имеет послед­ствия? Изменение температуры происходит главным

образом в направлении меридианов — от экватора к по­люсам. Оказывается, что величина этого изменения су­щественно зависит от площади, занятой в полярных районах материковыми и морскими льдами. Чем боль­ше эта площадь, тем ниже температура воздуха в по­лярных районах. Расчеты показывают, например, что льды Арктики понижают среднегодовую температуру на 15° С, а ледяной щит Гренландии вызывает отрица­тельную температурную аномалию в 16° С. Температу-

Морение и материковые льды

&

Осадки

Облачность

Атмосф.

ч77 ‘ 1 // 7*-^ _ Ср. температура поверхности

Температурные градиенты

Солнечная

‘О’ЛИ^ИЩ

О—г-

равиация Ср. т-ра

радиация

I &05ссь

воздуха

t

Испарение■

Рис. 19. Общая функциональная схема земная поверхность —

атмосфера (по С. Я — Сергину, 1966).

А — атмосфера, Я — поверхность планеты.

ра на поверхности открытого океана никогда не может упасть ниже—2° С. Вблизи границы вода — лед созда­ются значительные разности температуры — к центру ледяных массивов температура падает, и это падение пропорционально площади льдов (в центральных рай­онах Гренландии среднегодовая температура воздуха. —30°, Антарктиды —60°С). С другой стороны, повыше­ние температуры воды с удалением от льдов вызывается теплом Солнца и происходит тем быстрее, чем больше поступление этого тепла й, значит, чем ‘ ближе рас­положена к экватору граница льдов. Значит, темпера­турный градиент — величина переменная, зависящая от площади льдов и прежде всего льдов’ морских, посколь­ку площади материковых льдов (например, Антаркти­ды) ограничены размерами подстилающей твердой по­верхности. ‘ ‘ : ‘ ;

Таким образом, мы можем записать:

G=A(S

где G — средний для поверхности Земли градиент тем — — пературы, a S — средняя площадь, занятая льдом (мор­ским и матеоиковым). . ‘

С другой стороны, чем больше пространственное из­менение температуры поверхности, тем больше разнос­ти приземного давления атмосферы. Это происходит потому, что теплая поверхность нагревает воздух и уве­личивает высоту лежащего над ней слоя атмосферы. Холодная поверхность охлаждает воздух и атмосфер­ная оболочка над ней сжимается. На больших высотах происходят движения, в результате которых толщина атмосферы выравнивается за счет притока воздуха к холодным областям. Таким образом, к охлажденным поверхностям наибольших высотах стекаются дополни­тельные массы воздуха, которые создают области вы­сокого приземного давления. Над нагретыми поверх­ностями возникает обратная картина. Значит, большие разности приземной температуры создают большие градиенты приземного давления атмосферы. Но разли­чия давления:— это движущая сила, создающая призем­ный ветер. Чем больше разность давления, тем сильнее ветер. Мы можем записать зависимость ветра от гра­диента температуры:

(85)

W=f2(G),

где W — скорость ветра.

На рис. 19 эта связь показана линией «температур­ные градиенты». Нарастающая скорость ветра увели­чивает скорость испарения с поверхности океана. Эта связь показана линией «атмосферная циркуляция». Ис­парение увеличивает облачность и осадки. Осадки вли­яют-на образование снежных и ледяных покровов, ко­торые вместе с облачностью определяют альбедо пла­неты и с его помощью регулируют подачу солнечного тепла; . . . . •

На рис. 19 показана также связь между средней температурой поверхности океана и состоянием атмо­сферы. Эта, связь заключается в том, что подстилаю­щая поверхность нагревает атмосферу и этим путем

увеличивает ее возможность поглощать водяной пар без конденсации его в облачность и перехода в осадки. Нагревание океана сопровождается также выделением из него в воздух углекислого газа, который в раство­ренной и — химически связанной форме содержится в океане в значительно большем количестве, чем в атмо­сфере. Присутствие в воздухе двух газов — водяного пара и углекислого газа — очень сильно влияет на проз­рачность атмосферы относительно теплового излучения. Добавление этих газов делает пропускную способность атмосферы к тепловым лучам избирательной. Чем вы­ше температура тела, тем меньше длина его тепловых волн. Короткие волны солнечной радиации беспрепят­ственно проходят через воздух, содержащий водяные пары и углекислый газ, но длинные волны теплового излучения земной поверхности поглощаются этими га­зами. Таким образом создается парниковый эффект земной атмосферы.

Связи, показанные на схеме, были выражены урав­нениями и введены в электронную аналоговую модель. Это устройство позволило определять поведение систе­мы земная поверхность—атмосфера в ответ на различ­ного рода случайные возмущения на входе, т. е. в ве­личине поступления тепла. Причины этих возмущений могут быть разными. Это прямое изменение поступаю­щей радиации или изменения поглощаемого Землей тепла за счет изменений ее атмосферы и состояния по­верхности. —

Записи, снятые с электронной модели, показали из­менения во времени массы ледников и температуры земной ^поверхности (рис. 20). Эти изменения даны в отклонениях от среднего состояния.

В процессе подготовки модели было найдено, что не­которыми связями системы можно пренебречь ввиду их незначительной роли в энергетических процессах. Так, в модели земная поверхность представлена в двух состо­яниях— льды и океан. Суша учитывается косвенным образом — поправкой на испарение океана. Но изменения площади морских льдов оказались принципиально важ­ными.

Если в модель ввести линейную зависимость площа­ди льдов от температуры океана, то модель работает в затухающем колебательном режиме. Однако в реаль­
ном океане связь между температурой и площадью морских льдов весьма сложна, что вызвано соленостью морской воды. В противоположность воде пресной вода океана имеет максимальную плотность при температу­ре замерзания. Поэтому охлажденные частицы воды, становясь более тяжелыми, чем подстилающие их во­ды, уходят с поверхности, не успев превратиться в лед. Таким образом, началу замерзания в океане — должно предшествовать интенсивное плотностное перемешива­ние, которое задерживает рост ледяного покрова.

Рис. 20. Запись авто­колебаний системы земная поверхность — атмосфера (по С. Я — Сергину, 1968).

Палеогеографические данные показывают, что при охлаждении земной поверхности площадь морских льдов возрастала сперва быстро, затем все медленнее и медленнее, напоминая в своем изменении ход синусо­иды от 0 до я/2. Когда такая зависимость площади льдов от температуры вводилась в модель, изменения климата приобретали незатухающий автоколебатель­ный характер, как это. видно, например, из рис. 20. Ко­лебания здесь развиваются без участия внешнего воз­мущения, их источником служат отклонения парамет­ров системы от равновесного состояния. В начальный момент времени температура поверхности имеет сред­нее значение, но уменьшенная масса льдов не соответ­ствует этой температуре (на рисунке масса оледенения показана сплошной линией, а температура поверхности планеты — пунктирной). Такое несоответствие могло бы возникнуть при искусственном уничтожении ледяных щитов. В связи с этим несоответствием температура, как и предсказывают проекты уничтожения льдов, быстро повышается. Однако далекие последствия это­го весьма плачевны. Следя за рисунком слева направо, мы видим, что примерно через 25 тысяч лет развивает­ся новое оледенение Земли.

Системный анализ и математическое моделирование глобальных процессов — это вопросы для географии океана и суши относительно новые. В первой половине

нашего столетия моделированию подвергались преиму­щественно явления локального характера, связанные с развитием или условием равновесного состояния физи­ческих процессов в какой-то точке пространства.

Переходя последовательно от одной точки к другой, океанологи смогли рассчитать карты осредненных, в значительной степени идеализированных морских тече­ний и получить величины переносимого ими тепла и со­лей. Парадоксальным было, однако, то, что объяснить картину циркуляции было иногда труднее, чем рас­считать. Почему у западных берегов Атлантики суще­ствуют стремительный Гольфстрим, а у восточных — не­устойчивое и медленное движение вод, хотя поле ветра над океаном почти симметрично? Почему Гольф­стрим отрывается от берегов Северной Америки рань­ше, чем на него действуют западные отжимные ветры? Почему, пересекая затем ветровое поле, он устремляет­ся в полярные широты? Почему под ним существует глубинное противотечение? Не зная ответов на эти и другие вопросы, мы не можем предсказывать поведе­ние океанической системы. —

Мы рассмотрели наиболее простые модели, служа­щие фундаментом дальнейшего развития теории дина­мической системы океана. Эти модели еще не вошли ни в один из отечественных учебников океанологии или географии, а научные журналы публикуют все новые и новые работы, усложняющие моделирование и прибли­жающие его к реальным условиям планеты.

Таким образом, всякая обзорная работа, посвящен­ная современному моделированию океана, успеет в ка­кой-то мере устареть раньше, чем увидит читателей. Тем не менее понять новое нельзя без опоры на те ра­боты, из критики и усовершенствования которых это новое появилось в науке.

Комментарии запрещены.