Бурение грунтовых зондов, установка энергетических колодцев

Дисперсные системы обладают вязкостью, пластичностью, упругостью и прочностью — свойствами, которые получили на­звание структурно-механических. Эти свойства во многом опре­деляют эксплуатационные характеристики промывочных жидко­стей и тампонажных растворов.

Законы течения и деформации любого тела — предмет изу­чения реологии. Цель реологии — составить такую систему уравнений, которая бы связывала напряжения, деформации, ско­рости деформации и была применима для любых тел.

Любое тело изменяется, деформируется под действием внешних сил. Если деформация тела исчезает при устранении внешних сил, то тело и деформации называются упру­гими. Если тело после снятия нагрузки не принимает свою первоначальную форму, то это свидетельствует, что наряду с упругой деформацией существует и пластическая дефор­мация. Тело называется пластическим, если оно способно без разрушения переносить значительные пластические деформации, намного превосходящие упругие.

Поведение любого тела под воздействием внешних сил опре­деляется его внутренней структурой, величиной и скоростью воз­никновения напряжений, характером их изменения.

Коагуляционным структурам присуща сдвиговая высокая эластичность, которая имеется даже при жестких частицах дис­персной фазы, образующих пространственную сетку. Это связа­но с взаимной ориентацией анизодиаметричных частиц —пало­чек, пластинок или цепочек, образуемых изометричными части­цами в направлении сдвига. Каждому значению деформации сдвига соответствует определенная степень ориентации, непре­рывно возрастающая при деформации. Если напряжения, воз­никающие в коагуляционной структуре, не превышают предела текучести, при снятии нагрузки структура быстро восстанавли­вается. Высокоэластичные деформации коагуляционных струк­тур в тысячи раз и более превышают истинно упругие.

Оценка свойств промывочной жидкости, определяющих ее поведение при движении, связана в первую очередь с вяз­костью. Под вязкостью понимается свойство жидкости со­противляться относительному перемещению ее частиц. Таким образом, вязкость — мера внутреннего трения.

Рассмотрим движение жидкости между двумя параллельными плоскостями, одна из которых неподвижна, а другая перемеща­ется с постоянной скоростью И (рис. 3). Слой жидкости, приле­гающий к подвижной плоскости, будет перемещаться со ско­ростью И, А скорость частиц жидкости на неподвижной плоско­сти равна нулю. Движение от одного слоя жидкости к другому в направлении, перпендикулярном к движению, будет передаваться за счет сил внутреннего трения.

Чтобы сдвинуть одну плоскость относительно другой, нужно приложить к подвижной плоскости некоторую силу F, Равную силе трения. Согласно теоретическим положениям Ньютона, сила F Пропорциональна поверхности соприкосновения S, Ско —

Рости И И обратно пропорциональна расстоянию между плоско­стями П:

F = μSu/N. (I . 3)

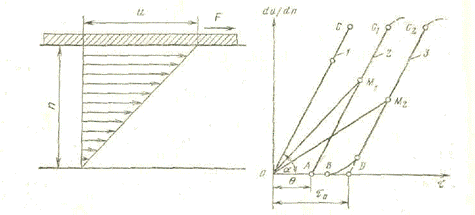
Рис. 3. Изменение скорости Рис. 4. Реологические кривые:

Жидкости по нормали. 1 — ньютоновская жидкость;

2 — Тело Бингама; 3 — тело Шведова

Если расстояние между двумя частицами рассматриваемого слоя жидкости бесконечно мало,

(I.4)

Если силу F Отнести к единице площади, то получится зна­чение так называемого касательного напряжения (закон жид­костного трения Ньютона)

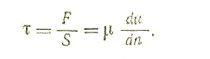(I.5)

Здесь μ — коэффициент внутреннего трения или динамиче­ской (абсолютной) вязкости; Du/Dn — градиент скорости сдвига.

Чаще μ Называется просто динамической или абсолютной вязкостью; размерность μ — Па•с.

Графически (рис. 4) закон Ньютона выразится прямой лини­ей ОС, Проходящей через начало координат с угловым коэффи­циентом Величина, обратная tgα, есть μ .

Жидкости, подчиняющиеся закону Ньютона, называются ньютоновскими. К ним можно отнести воду, истинные растворы, некоторые естественные промывочные жидкости и др. В систе­ме прямоугольных координат ньютоновские жидкости всегда ха­рактеризуются одним постоянным параметром — абсолютной вязкостью μ. Наряду с понятием абсолютной вязкости пользуют­ся и понятием кинематической вязкости v (в М2/с). Абсолютная и кинематическая вязкости связаны между собой отношением

V=μ/ρ, (I.6)

Где р — плотность промывочной жидкости.

Жидкости, течение которых отклоняется от закона Ньютона, получили название неньютоновских.

При введении дисперсной фазы в ньютоновскую жидкость до определенной величины объема вязкость будет увеличиваться и линейная зависимость между т и Du/Dn Не будет нарушаться. По А. Эйнштейну, вязкость такой дисперсной системы μд в зависи­мости от концентрации определяется по выражению

μД = μ(1+AСV), (I.7)

Где a — постоянный коэффициент, зависящий от формы частиц, для частиц круглой формы а = 2,5; СV — объемная концентрация дисперсной фазы.

Формула (I.7) получена в предположении, что раствор очень разбавленный, т. е. настолько, что расстояния между частицами весьма велики по сравнению с их размерами.

Однако при достижении определенного объема заполнения твердой фазы такая линейная зависимость нарушается, что вос­принимается как аномалия вязкости. В зависимости от вида дисперсной фазы и ее концентрации такие системы, часто назы­ваемые пластичными или вязко-пластичными, могут прибли­жаться по свойствам к жидким или твердым телам.

Благодаря возможности непрерывно восстанавливать разру­шенные контакты, дисперсные системы с коагуляционно-тиксо-тропной структурой способны при малых скоростях сдвига течь с высокой, но вполне измеримой вязкостью без заметного разру­шения внутренней структуры (ползучесть). С увеличением ско­рости сдвига не все разорванные связи успевают восстанавли­ваться, и тиксотропная система при каждом режиме течения ха­рактеризуется определенным динамическим равновесием между процессами разрушения и восстановления структуры. Зависи­мость прочности динамической структуры дисперсных систем от скорости сдвига и обусловливает непостоянство их вязкости, или аномалию вязкости.

Для того чтобы вывести тиксотропную промывочную жид­кость из состояния равновесия, требуется приложить определен­ное усилие. Поэтому на графиках (рис. 4) реологическая кривая таких жидкостей не проходит через начало координат и проч­ностные характеристики дисперсной системы можно оценивать количественно.

По Максвеллу, все реальные тела можно расположить в ряд между упруго-твердыми и маловязкими жидкостями по периоду релаксации. Под релаксацией понимают постепенное само­произвольное «рассасывание» упругих напряжений при постоян­ной деформации. Природа этого явления обусловлена непрерыв­ным хаотическим тепловым движением частиц тела, в результа­те которого рассеивается, переходя в тепло, запасенная при де­формировании упругая энергия. Период релаксации определяет время (в с), необходимое для уменьшения упругих напряжений в е раз (е — основание натуральных логарифмов). Период ре­лаксации

λ= μ/E (I.8)

Где Е — модуль Юнга.

Отношение времени действия силы к периоду релаксации оп­ределяет поведение данного тела, как твердого, так и жидкого. При этом любая жидкость может рассматриваться как упругое тело, если время действия силы намного меньше периода ре­лаксации. Напротив, твердое тело обнаруживает способность течь, если время действия силы больше периода релаксации.

Можно было бы, например, ходить по воде, не погружаясь в нее, если бы время каждого шага не превышало периода ре­лаксации для воды, т. е. ничтожно малой величины по сравне­нию с измеримыми (для воды μ=0,001 Па•с, E=1•1010 Па, λ= 1•10-13 с). Для более вязких жидкостей периоды релакса­ции вполне измеримы. Напри­мер, для битумов и асфальтов их можно непосредственно из­мерить.

Рис. 5. Механические модели тел:

А — Упругое тело; 6 — вязкое тело; В — пластичное тело; Г — Вязко-пластичное тело

Следовательно, период ре­лаксации — основная констан­та, объединяющая свойства твердого тела и жидкости. Пе­риод релаксации имеет боль­шое значение для оценки ус-стойчивости промывочных жидкостей и нетвердеющих тампонажных растворов в трещинах горных пород при борьбе с по­глощениями.

Все дисперсные структурированные системы в реальных ус­ловиях обладают различными упругими, вязкими, пластически­ми свойствами. Желая подчеркнуть преобладание одних свойств над другими, вводят соответствующие названия тел (систем): уп­ругое, упруго-вязкое, упруго-вязко-пластичное, вязко-пластичное и т. д.

Судить о характере деформационных процессов, протекаю­щих в системе, позволяют механические модели, которыми ус­ловно представляют реальные жидкости или тела. Модели отра­жают наиболее существенные свойства реальных тел. Упругое тело изображается пружиной, мгновенно изменяющей длину в за­висимости от величины приложенной силы (рис. 5, а), Вязкое тело моделируется невесомым поршнем, свободно двигающимся в цилиндре с вязкой жидкостью (рис. 5,6). Пластическое тече­ние моделируется элементом сухого трения — ползуном (рис. 5, в). Более сложные реологические тела моделируются комбинацией приведенных моделей, например, вязко-пластичное тело состоит из параллельно соединенных поршня и ползуна (рис. 5,г). Каждое тело (модель) получило название по имени первого исследователя.

Количественную оценку деформационного и релаксационного процессов дисперсных систем, объединяющих все промывочные жидкости и тампонажные растворы, дают константы обобщенно­го уравнения Максвелла — Шведова и Кельвина. Относитель­ная деформация, развивающаяся за время T При нагрузке Р = Const,

(I.9)

Здесь Е1 – условно-мгновенный модуль упругости, соответст­вует быстрой эластической деформации ε’о, развивающейся под действием нагрузки Р И исчезающей после разгрузки; Е2 — Эла­стический модуль, характеризующий способность системы к мед­ленным эластическим деформациям ε’2 , развивающимся после завершенной условно-мгновенной деформации; PK1 — ус­ловно-статический предел текучести, при напряжениях ниже пре­дела текучести наблюдается упругость, упругое последействие и весьма замедленное течение с максимальной вязкостью; η1— наибольшая пластическая вязкость; η2— вязкость упругого пос­ледействия, определяющая интенсивность развития эластической деформации.

Согласно уравнению (I.9), относительная суммарная дефор­мация состоит из быстрой эластической ε0/ = Р/Е1 Медленной эластической ε/2 = Р/Е2 И пластической деформации εT =

= .(P—Pki)/η1t

Используя приведенные константы физико-химической меха­ники дисперсных систем, можно для любого технологического процесса получить величины основных структурно-механических характеристик: эластичности Э=Е1/ (Е1 + Е2), Пластичности PK1/ η1 и периода истинной релаксации λ.

По соотношению величин деформаций εо, ε2 И ε1t можно на научной основе оценить устойчивость дисперсной системы и ее пригодность для нужд бурения. Однако получение такой инфор­мации довольно сложно и требует высокой квалификации ис­следователя. Поэтому в прикладных исследованиях описание деформационных процессов, происходящих в дисперсных систе­мах, упрощают.

Считается, что все структурированные промывочные жидко­сти и тампонажные растворы относятся либо к пластичным (телу Бингама), либо к вязко-пластичным (телу Шведова) жид­костям. Реологическая зависимость этих систем на графиках (см. рис. 4) не проходит через начало координат. Величина ка­сательного напряжения, при котором структурированная дис­персная система выходит из состояния равновесия и начинает двигаться, получила название предельного статического напря­жения сдвига 9 (в Па). Поскольку структура жидкости после перемешивания восстанавливается не мгновенно, величина 9 может значительно изменяться в зависимости от продолжитель­ности пребывания жидкости в покое. Как правило, в большин­стве структурированных промывочных жидкостей структура полностью стабилизируется в течение 10—15 мин. В тампонаж­ных растворах прочность структуры растет до окончания твердения (упрочнения) так как этот процесс сопровождается хими­ческим взаимодействием компонентов.

Правильное описание напряжений сдвига для структуриро­ванных систем имеет важное значение как для оценки гидрав­лических сопротивлений, так и для обеспечения нормальных ус­ловий очистки забоя скважин от выбуренной породы.

Зависимость, предложенная Бингамом, имеет вид (см. рис. 4, прямая АС)

Где τ — приложенное касательное напряжение, Па; θ — предель­ное статическое напряжение сдвига (для краткости его принято называть статическим напряжением сдвига); η — коэффициент структурной вязкости (или структурная вязкость), Па•с.

Зависимость (1.10) означает, что сопротивление сдвигу смеж­ных слоев структурированной дисперсной системы следует рас­сматривать как сумму двух величин:

1) напряжений, не зависящих от скорости сдвига;

2) напряжений, пропорциональных градиенту скорости сдви­га и подобных вязкостным напряжениям в обычных жидкостях.

Таким образом, жидкость, подчиняющаяся закону трения Бингама, характеризуется двумя параметрами: θ и η.

Зависимость ВС2 (см. рис. 4) представляет собой форму рео­логической кривой жидкостей, относящихся к телу Шведова, Она состоит из двух участков: криволинейного и прямолинейно­го. Размеры и форма криволинейного и угол наклона прямоли­нейного участка реологической кривой могут быть различны, и, строго говоря, для каждой жидкости должна быть найдена своя характерная зависимость:

Без существенного ущерба для практики сложную зависи­мость ВС2 Представляют прямой линией DC2, Полученной про­должением прямолинейного участка до пересечения с осью каса­тельных напряжений. Прямая DC2 Выражает обобщенный закон трения Шведова — Бингама:

Здесь τ0 — динамическое напряжение сдвига.

Динамическое напряжение сдвига — понятие условное, так как эту величину измерить непосредственно на каком-либо при­боре невозможно. Она может быть определена либо графиче­ским (отрезок OD), Либо расчетным путем.

В большинстве случаев динамическое напряжение сдвига больше статического θ, однако бывает и наоборот. Это свиде­тельствует о более сложном характере поведения дисперсных си­стем. Наибольшее расхождение между τ0 и θ в дисперсных си­стемах с значительным содержанием высококоллоидных фрак­ций.

Таким образом, уравнение (1.11) дает упрощенное описание зависимости градиента скорости течения от напряжения сдвига для вязко-пластичной жидкости. Для более полной характери­стики реологической кривой необходимо знать три постоянных параметра θ, τ0, η.

Имеется обобщенная характеристика вязкостных свойств структурированных дисперсных систем, которая учитывает пластические свойства этих систем в соответствии с законом Шведова — Бингама. Если (согласно закону Ньютона) опреде­лить вязкость как отношение величины приложенного касатель­ного напряжения к величине градиента скорости сдвига, то уравнение (I.10) можно представить в следующем виде:

Или

Обозначив

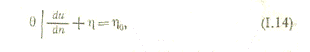
Получим

Где ηо — эффективная вязкость.

Графически (см. рис. 4) η0 Выражается величиной, обратной коэффициенту наклона прямой, проведенной из начала коорди­нат к любой точке (например, М1,М2) реологических кривых {АС1 И ВС2). В отличие от величины т], которая остается посто­янной на всем протяжении участка АС1 И DC2,Величина ηО Будет меняться в каждой новой точке.

Соответственно для кривой, характеризующейся зависи­мостью (I.11), значение эффективной вязкости.

Зависи­мостью (I.11), значение эффективной вязкости

Эффективная вязкость с ростом градиента скорости сдвига изменяется от вязкости практически не разрушенной структуры до вязкости предельно разрушенной структуры, которая опреде­ляется главным образом вязкостью дисперсионной среды. На­пример, для глинистых растворов вязкость практически не раз­рушенной структуры составляет миллионы Па•с, а вязкость пре­дельно разрушенной структуры — сотые и десятые доли Па•с, т. е. теоретический диапазон изменения эффективной вязкости чрезвычайно широк.

Практически значимый диапазон изменения эффективной вяз­кости гораздо меньше, так как стадия изменения ее от практиче­ски не разрушенной структуры до какого-то промежуточного со­стояния разрушения проходит в момент начала течения дисперс­ной системы мгновенно.

В гидравлических расчетах, связанных с течением вязко-пластичных жидкостей в трубах, η0 =η+ τ0D/6и, (I.17)

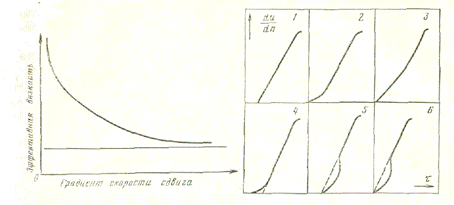
Рис 6. Общий вид зависимости эф — Рис. 7. Реологические зависимости

фективной вязкости от градиента неньютоновских жидкостей:

скорости сдвига 1 — Пластичная; 2 — Псевдопластичная;

3 —неньютоновская; 4 — Вязко-пластичная жид­кость;

5 — тиксотропно-пластичная жид­кость;

6 — тиксотролная

Где D — диаметр трубы (потока жидкости); И — средняя ско-рость движения жидкости.

Приближенный характер изменения эффективной вязкости глинистого раствора с ростом градиента скорости сдвига показан на рис. б.

Эти упрощенные представления о характере деформации в дисперсных системах позволяют более оперативно получать простые параметры, которые можно использовать при оценке техно­логических свойств промывочных жидкостей и тампонажных смесей, а также при гидравлических расчетах.

За рубежом реологическую зависимость для промывочных жидкостей представляют в степенном виде. Так, по Р. И. Уол-керу,

Где Т И R — константы изучаемой промывочной жидкости, опре­деляемые опытным путем.

Коэффициент Т Характеризует консистенцию раствора и по­зволяет интерпретировать его вязкость. Показатель степени R Характеризует отклонение поведения жидкости от ньютоновской.. Для воды и других ньютоновских жидкостей r-1.

Коэффициенты ТиRОпределяются графическим методом, для чего строится график τ=F(Du/Dn). Для определенных значе­ний градиента скорости сдвига находятся Т, А R Определяют по углу наклона кривой.

И. Н. Гуднин предлагает использовать обобщенное уравне­ние:

Которое, по его мнению, более точно отражает действительную взаимосвязь напряжений сдвига и других параметров структури­рованных систем.

Все это свидетельствует о том, что в описании поведения структурированных систем ученые не пришли пока к единому мнению. В бурении до сих пор пользуются наиболее простым описанием — законом Шведова — Бингама и вытекающими из него зависимостями. Это, конечно, не исключает использования других закономерностей.

В заключение необходимо отметить, что термин «неньютоновская жидкость» охватывает целую группу жидкостей, реологиче­ские зависимости которых отклоняются от прямолинейной, вы­ходящей из начала координат. На рис. 7 приведены реологиче­ские зависимости некоторых неньютоновских жидкостей, свиде­тельствующие О Сложности явлений, происходящих в промывоч­ных и тампонажных системах при деформации, и о приближен­ности их описания.

Комментарии запрещены.