Бурение грунтовых зондов, установка энергетических колодцев

Совместное влияние G и п на механическую скорость проход­ки выражается обычно уравнением вида

vu = a„fixnb. (66)

Как правило, и Ь^.1, но преобладают значения х~ и

&< 1. С ростом скорости вращения долота величина b обычно

уменьшается. По американским данным, относящимся к роторно­му бурению, х = 1—1,2 и выше, b = 1—0,5 и ниже.

В последние годы все большее распространение в практике бурения скважин получает уравнение вида

ом = a (G — С) пу, (67)

которое является общим случаем для формулы (54). Очевидно,

с• апУ, (68)

и для данной скорости вращения долота с* = const. Формула (67) удобна при проектировании режимов бурения и для прогно­зирования механической скорости проходки. Она довольно проста и обеспечивает достаточную для практики точность. ‘

Выше отмечалось, что в определенных пределах изменения G характер зависимости vM=vM(G, n) качественно одинаков по дан­ным экспериментов различных авторов. При выводе формулы (67) воспользуемся типичными данными [83], результаты обработки ко­торых представлены на рис. 11 и в табл. 2 и математически вы­ражены уравнением (60).

Анализ указанного материала показывает, что с увеличением G коэффициенты В и р в формуле (60) возрастают; при росте п уменьшается si; с увеличением G усиливается отрицательное влия­ние п на sp, чем больше G, тем выше Si при прочих одинаковых условиях; снижение si с ростом п можно компенсировать повыше­нием G. Зависимости В и р от G следуют линейному закону и могут быть выражены уравнением

TOC o "1-5" h z 5 (или Р) = цй — Ц. (69)

Если не учитывать данные для G —2 тс и выражать G в тон­нах, то для условий, эксперимента цв = 0,684, Дв = 1,174, щ =0,152

и Др = 0,34.

Учитывая выражение (69), записываем формулу (60) в сле­дующем виде: 1

Sl’=ai(G-C), (70)

где

= Цв — Ча lg п (71)

цв-ц^ gn

Oi

Подставим значение si в уравнение (2)

vM = 0,06ах(G — С) п a2(G — С) п.

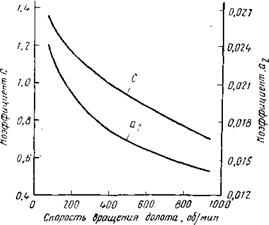
Графики зависимости й2 и С от скорости вращения долота представлены на рис. 15, из которого видно, что и йг и С умень-

шаются с ростом п. Зависимость от п хорошо описывается уравнением

а

(74)

Внеся это значение аг в формулу (73) и обозначив

у = 1 — 62,

получим уравнение (67). Для условий эксперимента а = 0,0648, &г = 0,223 и у = 0,777; для условий бурения в сланцах на юге Луи­зианы у — 0,6. — ч

При объемном разрушении породы и отсутствии влияния огра­ниченности высоты зубьев и степени очистки забоя на разрушение породы величина С тем больше, чем тверже порода. При поверх­ностном разрушении С=0. Чем сильнее влияние зашламленности забоя и чем больше сказывается ограниченная высота зубьев, тем меньше параметр С, крторый может стать и отрицательной вели-1
*П1ной (при этом знак минус в формуле (67) сменится на знак плюс).

При использовании формулы (67) в практических расчетах ве­личина С принимается постоянной даже применительно к турбин­ному бурению, а из выражения (72) следует, что с ростом п ве­личина С уменьшается. Поэтому возникает вопрос о применимо­сти формулы (67) для условий турбинного бурения.

Как видно из рис. 15, при увеличении п в 9 раз параметр С уменьшается в 1,8 раза. Очевидно, при изменении п в пределах рабочих режимов работы турбобуров влиянием п на С можно Пренебречь, если определять значение С для некоторой средней ft.

Учитывая, что С зависит от п, желательно находить парамет­ры уравнения (67) по данным роторного бурения или буревдр электробурами. Методика определения указанных параметров й§- Ложена в работе [23]. ’

Комментарии запрещены.