Аппаратурные принципы радиогеодезических систем
Аппаратурные принципы радиогеодезических систем
В предыдущем разделе мы касались лишь геометрических принципов работы РГС, не интересуясь вопросами их технического осуществления.
Рассмотрим теперь радиогеодезические системы с аппаратурной точки зрения, обратив внимание в первую очередь на физические и технические принципы их работы.
Как явствует из классификационной табл. 10, по характеру излучения РГС подразделяются на импульсные и с непрерывным излучением радиоволн, а по методам измерений — на временные, фазовые и фазово-временные. Во временных системах всегда используется импульсное излучение, поэтому термин «импульсная система» однозначно определяет как характер излучения, так и метод измерения. В чисто фазовых системах используется непрерывное излучение, в фазово-временных — импульсное. .
В импульсных системах прямым образом реализуется временной (импульсный) метод, рассмотренный в § 3. Импульсные системы могут быть как круговыми, так и гиперболическими. Основной недостаток импульсных систем — сравнительно большая абсолютная ошибка, присущая импульсному методу измерения расстояний. Поэтому их выгодно использовать при больших дальностях, когда относительная ошибка измерений невелика.
В последнее время, однако, достигнут значительный прогресс в отношении точности импульсных систем благодаря применению корреляционных методов аппаратурной обработки импульсных сигналов.
Фазово-временные системы, называемые также импульснофазовыми, выделились в отдельный самостоятельный класс РГС. В таких системах импульсы излучения представляют собой радиоимпульсы с некоторой частотой заполнения. Для разрешения неоднозначности обычно используются временные измерения импульсным методом, а для точного определения — фазовые измерения на частоте заполнения.
Подавляющее большинство РГС являются фазовыми.
Перейдем к рассмотрению общих принципов построении аппаратуры фазовых РГС. Существуют два основных вари-. анта такого построения — когерентный и некогерентный (гетеродинный).
 Когерентные фазовые системы. Это системы без модуляции, в которых фазовые измерения производятся на несущих частотах. Такие системы могут быть построены с использованием частотного или временного разделения каналов, обеспечивающего возможность раздельного приема на подвижной станции колебаний от базисных станций. Рассмотрим, например, системы с частотным разделением, основанным на идее когерентного преобразования частоты, осуществляемого путем умножения частоты на некоторый целесообразно подобранный коэффициент. Такие системы могут быть как круговыми, так и гиперболическими. •
Когерентные фазовые системы. Это системы без модуляции, в которых фазовые измерения производятся на несущих частотах. Такие системы могут быть построены с использованием частотного или временного разделения каналов, обеспечивающего возможность раздельного приема на подвижной станции колебаний от базисных станций. Рассмотрим, например, системы с частотным разделением, основанным на идее когерентного преобразования частоты, осуществляемого путем умножения частоты на некоторый целесообразно подобранный коэффициент. Такие системы могут быть как круговыми, так и гиперболическими. •
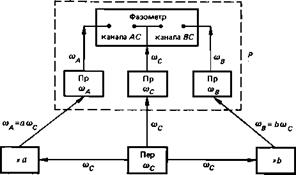
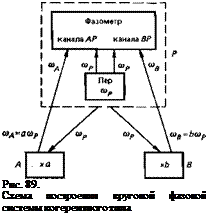
Круговая когерентная система. Принцип построения круговой системы с когерентным преобразованием частоты показан на рис. 89. Передатчик подвижной станции Р излучает колебания частоты ар. Эти колебания принимаются на базисных станциях А и В, где происходит умножение частоты на различные коэффициенты а и b и передача обратно на станцию Р. Таким образом, на подвижную станцию приходят сигналы с различными частотами tiu = fl(Op и ав=Ьар[32]. Двухканальный фазометр измеряет по каждому каналу разность фаз пришедшего сигнала и опорного сигнала от своего передатчика. Как видно из рис. 89, в каждом канале необходимо измерить разность фаз сигналов различных частот: ал и ар в канале АР и ав и top в канале ВР. Обычно для осуществления фазовых измерений сигналы по каждому каналу приводят к какой-то одной частоте, умножая частоту одного из поступающих на фазометр сигналов на соответствующий коэффициент.
Для ослабления помех от гармоник коэффициенты а и b выбирают равными не целым числам, а дробным, например 2/3, 3/2, 3/4, 4/3 и т. д. В частном случае Ь=1/а, например, а=2/3, 6 = 3/2.
Рассмотрим работу одного из каналов, скажем, канала АР.
Колебания частоты сор, пришедшие на станцию Л, приобретают фазовый сдвиг q? i = щ—АР • Колебания частоты со а при распространении до станции Р получают сдвиг <р2 = а>л • Суммарный фазовый сдвиг, который должен быть измерен фазометром, равен
фир = фі + фг = Ир-^£- + «>л-?^£— (4-47)
Пусть колебания приводятся к частоте юл, Для чего сигнал частоты юр перед подачей на фазометр умножается по частоте на а=сол/сор. Так как при умножении частоты умножается и фаза, то получаем
![]() Флр = ©я = 2©л
Флр = ©я = 2©л
V (Dp V V
Аналогично для второго канала ВР, приводя сигналы, например, к частоте toр (умножением сигнала ©в на 1 /& = юр/о»в), получим
При перемещении станции Р расстояния АР и ВР непрерывно изменяются и соответственно изменяются разности фаз (4.48) и (4.49). Очевидно, что приращениям расстояний Дглр и Лгвр соответствуют приращения разности фаз
Афлр = 2<0л = -^-АгАР (4.50)
V *А
Афвр = 2юр—= ——А ГдР. (4.51)
V Ар
Из этих равенств следует, что при изменении расстояний на половину длины волны разность фаз меняется на 2я, т. е. на один фазовый цикл. Поэтому, если при движении станции А осуществлять непрерывную регистрацию фазовых циклов, то для получения изменения расстояний по каждому каналу достаточно зарегистрированное число фазовых циклов М, в общем случае нецелое, умножить на половину длины волны:
А Гар = Мар.-^-; (4.52)
&rBP = MBP—£-• (4.53)
Так как M = N+AN, где N—целое число фазовых циклов,
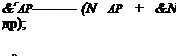 |
|
AN— дробная часть цикла, то
и в этих формулах мы узнаём обычные уравнения фазовой дальнометрии, примененные к случаю движущегося объекта.
Гиперболическая когерентная система. Если в круговой системе, изображенной на рис. 89, на подвижной станции Р оставить только приемно-фазометрическую аппаратуру, а передатчик отделить и разместить его в неподвижной точке С между станциями А и В, то мы получим гиперболическую систему с центральной базисной станцией С (рис. 90). Станция С излучает колебания частоты ©с, а на отражающих станциях А и В происходит прием и преобразование этой частоты совершенно так же, как и в круговой системе. Поэтому работа гиперболической когерентной системы аналогична работе круговой системы с той разницей, что из-за другого расположения передатчика в формулах для разностей фаз будут фигурировать не расстояния, а разности расстояний: гАР— гСР в одном канале и гВР — гСР в другом канале, и в окончательном результате для приращений разностей расстояний получаются следующие соотношения:
![]() А (гар—i’qp) — ^-b (Ni + &N і); &(гвр—r qp) = (N H + AN n),
А (гар—i’qp) — ^-b (Ni + &N і); &(гвр—r qp) = (N H + AN n),
где индексы I и II относятся к каналам базисов АС и ВС.
Так как в гиперболической системе подвижная станция только приемная, то такие системы могут работать с неограниченным количеством подвижных станций (фазовых зондов), называемых часто приемоиндикаторами.
Для определения N и AN при способах радиолага и фазового зонда могут быть использованы цифровые счетчики (индикаторы), ведущие непосредственный счет фазовых циклов. Иногда используется и более «старый» метод графической регистрации фазовых циклов, при котором сигналы с фазометров обоих каналов подаются на регистратор, ведущий двухканальную запись фазовых циклов в виде штрихов на бумажной ленте или фотопленке (фазограмме), на которую также наносятся метки в момент нахождения подвижной станции в исходной и определяемой точках. Величины N и AN находятся путем подсчета количества полных штрихов и оценки дробной доли штриха на интервале между соответствующими метками. Предусматривается также возможность определения знака приращения (по наклону штрихов).
|
с Рис. 90. Схема построения гиперболической фазовой системы когерентного типа |
Как уже упоминалось ранее, если в аппаратуре РГС предусмотрено несколько «комплектов» рабочих частот (многочастотные системы), то в этом случае число N определяется по результатам измерений на всех этих частотах (аналог способа фиксированных частот, см, § 4,глава 1).При этом не требуется геодезической привязки исходной точки маршрута, но надо приближенно знать координаты подвижной станции. Известны и другие (аналитические) методы разрешения неоднозначности [8].
Некогерентные фазовые системы. В когерентных системах требование жесткой связи частот передающих станций заставляет принимать специальные меры по поддержанию этой связи. При разбалансе частот нарушаются фазовые соотношения, и поэтому станции снабжаются дополнительной аппаратурой контроля и подстройки (системами фазовой подстройки частоты). Другими словами, в когерентных РГС необходима постоянно поддерживаемая синхронизация станций.
Этот недостаток полностью устраняется в некогерентных фазовых системах, принципиально не требующих синхронизации передающих станций, которые могут работать совершенно независимо друг от друга. Такая независимость (некогерентность) стала возможной благодаря использованию принципа гетеродинирования, почему некогерентные системы называют также гетеродинными. С применением гетеродинирования в ра — диодальномерных устройствах мы уже неоднократно встречались ранее — при рассмотрении основ фазового метода (§ 4) и в геодезических радиодальномерах (§ 19). Здесь мы кратко остановимся на применении гетеродинного принципа к построению радиогеодезических систем. Использование гетеродинирования в РГС, помимо ликвидации необходимости синхронизации станций, позволяет также выполнять фазовые измерения на низкой частоте со всеми вытекающими отсюда преимуществами.
Как должна быть построена гетеродинная радиогеодезическая система? Известно несколько вариантов ее построения. Во-первых, она может быть круговой или гиперболической. Во-вторых, в ней может использоваться модуляция излучаемых колебаний.
Круговая некогерентная УКВ-система. Из круговых гетеродинных РГС мы ограничимся рассмотрением систем с модуляцией, построенных на основе схемы УКВ-радиодальномера (типа теллурометр) *. Эта схема подробно разбиралась в § 19, и здесь нет необходимости на ней останавливаться. Напомним лишь, что радиодальномер состоит из двух неподвижных станций— ведущей и ведомой, имеющих различные несущие частоты, модулируемые различными масштабными частотами, и измерения выполняются на низкой частоте, равной разности масштабных частот станций и образующейся в результате гетеродинирования несущих частот с последующим детектированием.
Чтобы на основе такого радиодальномера построить круговую радиогеодезическую систему, необходимо:
— ведущую станцию (точнее, ее приемную часть) сделать двухканальной, способной работать одновременно с двумя ведомыми станциями, имеющими различные несущие частоты;
— поместить ведущую станцию на подвижной объект, а ведомые станции установить в пунктах с известными координатами, т. е. разнести на концы базиса круговой системы.
Разумеется, при этом нужно предусмотреть целый ряд технических деталей — автоматическое синхронное переключение масштабных частот на всех станциях, метод регистрации разности фаз по каждому каналу (например, цифровой или записью на фазограмме) и т. п.; эти вопросы могут быть решены в конкретных системах различным образом.
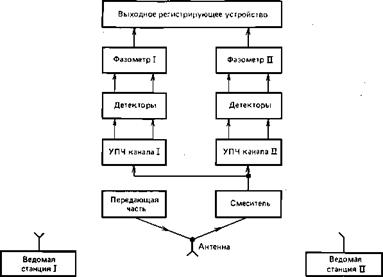
Двухканальность ведущей станции может быть обеспечена при общей антенне и смесителе применением двухканального усилителя промежуточной частоты и последующего раздельного детектирования по обоим каналам (рис. 91).
Круговые системы, построенные на изложенном принципе, обладают двумя очень важными преимуществами. Во-первых, они позволяют измерять сразу сами расстояния, а не их приращения, поскольку неоднозначность разрешается в процессе измерений применением нескольких масштабных частот. Во-вторых, и это еще более важно, они являются наиболее высокоточными из всех типов радиогеодезических систем, что обусловлено использованием схемы геодезического радиодальномера УКВ-диапазона. .
, , * Существуют также круговые гетеродинные РГС без модуляции — например, система Торано 0; подробное ее описание можно найти в [8].
|
Рис. 91. Общая схема круговой гетеродинной системы на основе радиодальномера |
К настоящему времени разработано несколько таких систем, основные данные которых приведены в конце настоящего параграфа.
Гиперболическая некогерентная система. В некогерентных системах гиперболического типа фазовые измерения выполняются на низкой частоте, образованной гетеродинированием немодулированных (несущих) частот станций. Следует отметить, что модуляция в таких системах частично используется, но она играет вспомогательную роль, являясь средством передачи (ретрансляции) низкочастотного сигнала.
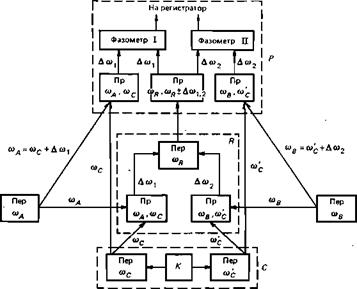
Рассмотрим работу гиперболической гетеродинной системы на примере широко применяемой в СССР системы «Поиск» [33]. Ее блок-схема показана на рис. 92. Система работает в режиме фазового зонДа и измеряет приращения разностей расстояний. Всего в системе пять станций: три базисных — А, В и С, подвижная станция (фазовый зонд) Р и еще одна станция R — ретранслятор. Станции работают в частотном диапазоне 1,6-=- — т-2,5 МГц. На центральной базисной станции С имеется сдвоенный передатчик, излучающий попеременно частоты ©с и ю’с — Попеременный режим обеспечивается коммутатором К, поочередно (4—6 раз в секунду) подключающим антенну к соответствующему генератору. На боковых базисных станциях А и В
|
Рис. 92. • Блок-схема фазовой гетеродинной гиперболической системы «Поиск» |
имеются передатчики, непрерывно излучающие частоты ©А и ©в соответственно. При этом ©а = ©с+Аса і, ©в=юс’+А©2, где Дюі и Д©2 — низкие частоты (численное значение их составляет обычно 460 и 660 Гц). Излучение базисных станций принимается как на подвижной станции Р, так и на ретрансляционной станции R, и в соответствующих приемниках происходит смешение принимаемых частот (гетеродинирование), в результате которого соответствующей фильтрацией выделяются колебания низких частот А©і (в первом канале) и Д©2 (во втором канале). На ретрансляторе частотами А©і и Д(о2 попеременно модулируется несущая передатчика ©я. Модулированное излучение ретранслятора принимается на подвижной станции и детектируется. Таким образом, в первом канале образуются два сигнала частоты Д©ь а во втором канале —два сигнала частоты Д©2. Эти низкочастотные сигналы в каждом канале поступают на фазометр. .
Рассмотрим работу первого канала (соответствующего базису АС). Текущие фазы колебаний, излучаемых передатчиками станций А и С, можно представить выражениями
фл = ю^ + <рл; (4.58)
ФС = ©с< + ф“, (4.59)
где ф° — соответствующие начальные фазы. Излучение от станций А и С принимается на подвижной станции Р и на ретран
сляторе R. Фазы колебаний, пришедших в Р, будут равны
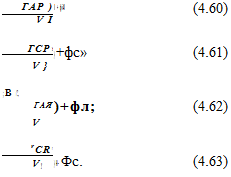 Фея;
Фея;
В приемниках станций Р и R происходит смешение колебаний, пришедших от Л и С, и образование сигналов разностной частоты Д(0] =о)а — ©с, выделяемых низкочастотными фильтрами. Фазы этих сигналов, очевидно, будут равны:
фр=ф-4р — фер = Д©1*— ~^~ + +(фл — фс);
• V V
(4.64)
Фя = фля—Фея = -^-+ (фд—фс)-
(4.65)
Сигнал с фазой фр на станции Р подается на один вход фазометра. Сигнал же с фазой фн передается из R в Р модуляцией по ретрансляционному каналу и подается на второй вход фазометра. При этом за счет передачи его фаза становится равной Фяр = Фя—А(ох Trp ■, т. е.
Фяр = Дю^—©л-^- + ©с-^- — Д®і-^-+(фл—Фс)-
(4.66)
Таким образом, фазометр первого канала определяет разность фаз
Фі = Фя—Фяя= — (®с + Д©і)-^+ ©с-^-+©л-^—®сХ
V V V
Х^+Ащ_ГЕР_ + ь= ГСР-ГАР _ ГАР-ГЦР _
V V О V v
+ (4.67)
V V
где через г|)і обозначены дополнительные, не поддающиеся учету фазовые задержки, неизбежные в реальной аппаратуре.
Так как выражение (4.67) не содержит начальных фаз ф°а и <р°с, то базисные станции не нуждаются в синхронизации.
Из (4.67) видно, что разность фаз <pi зависит от разности расстояний от фазового зонда до центральной и боковой станций гср — гАР. Именно эта зависимость положена в основу измерений. Однако, как видно из формулы, <pi зависит еще от нескольких линейных величин: расстояний Гея, rAR и разности расстояний гАР—rRp, а также от неизвестной нам величины фі-
Рассмотрим, что будет происходить при движении станции Р. Так как расстояния от базисных станций до ретранслятора Ген и гад постоянны, то содержащие их члены не будут изменяться при движении фазового зонда. Величина фі определяется фазовыми задержками в аппаратуре, а также искажениями фазового поля у антенн из-за влияния подстилающей поверхности. Ее возможные изменения не могут быть надежно учтены, и она обычно принимается за величину постоянную. Таким образом, три последних члена в (4.67) при движении станции Р не будут изменяться. Поэтому, если станция переместилась из одной точки в другую, то регистрируемое приращение разности фаз будет, очевидно, определяться выражением
АФ[ = <вс А {гср~ГАр) -А(ох А {ГАР~ TRp) . (4.68)
Выражая приращение разности фаз в фазовых циклах, перепишем (4.68) в виде
2ЛМ + АNx) = *q М’ср-мр) _Дй)1 ММр-гдр) t (4>69)
V V
откуда для приращения разности расстояний найдем
А {гср—глр) — (Nі + АЛ^) + ——— А (гар—гRP),
сое ®с
или
А (гСр—rAp) = Xc(Nl + bNi) + А 1 А (гар — rRp)- (4-70)
(DC
Точно так же можно получить выражение для приращения разности расстояний по второму каналу
А (гср—гвр) ~ (Nu + АЛ^и) Н—————————- А (тВР — гRP). (4.71)
CDc
Так как Дші<(Ос, Acd2<(o’с, то вторые члены в этих равенствах имеют небольшую величину. Они гораздо меньше первых членов и считаются поправочными. При работах, не требующих высокой точности, их вообще не учитывают. В случае необходимости (при аэрофотосъемочных работах) они могут быть определены по приближенным значениям величин (гар — Глр) и (Гвр — Глр).
Числа N и AN определяются по записи фазовых циклов, выполняемой двухканальным регистрирующим устройством. В последних модификациях системы «Поиск» используются также цифровые счетчики фазовых циклов и различные устройства для автоматизации измерений вплоть до выдачи координат на печать и вычерчивания курса фазового зонда [2, 8].
Заканчивая на этом обзор основных аппаратурных решений, отметим одно перспективное направление — использование так называемого бортового хранения фазы опорного сигнала, позволяющее строить системы с односторонней связью между передатчиком и приемником в каждом канале и, в частности, сделать ненужной ретрансляцию опорных низкочастотных сигналов в гетеродинных системах типа «Поиск». В системах с бортовым хранением фазы на подвижной (приемной) и базисных (передающих) станциях устанавливаются исключительно высокостабильные генераторы — атомные стандарты частоты, допускающие строгую синхронизацию друг с другом. Тогда генератор на подвижной станции будет сохранять начальную фазу колебаний, излучаемых передатчиком базисной станции, т. е. будет служить опорным генератором, и фазометр на подвижной станции включается между этим генератором и приемником, принимающим излучение от базисной станции. Таким образом, на подвижной станции становится возможным измерение фазового сдвига колебаний, прошедших только в одном направлении от базисной станции до подвижной. Чем выше стабильность частоты используемых атомных стандартов, тем продолжительней может быть работа системы (расфазировка, обусловленная нестабильностью частоты порядка 10~12 за 1 ч, приводит к линейной ошибке порядка нескольких метров за каждый час работы). В системе с бортовым хранением фазы одна наземная станция может работать с любым количеством подвижных станций, находящихся в радиусе ее действия. Примером системы с бортовым хранением фазы может служить круговая гетеродинная система Торан О, в которой используется рубидиевый эталон частоты со стабильностью примерно 2 • 10“12 за 1 ч.