ЧАСТОТНЫЙ МЕТОД
ЧАСТОТНЫЙ МЕТОД
Сущность метода. Частотный метод измерения расстояний основан на использовании частотно-модулированных (ЧМ) колебаний и сводится к измерению приращения частоты за время распространения ЧМ сигнала до отражателя и обратно, т. е. на расстояние 2 D. Если частота / излучаемого колебания изменяется по линейному закону, т. е. непрерывно увеличивается или уменьшается с постоянной скоростью y=df/dt, то изменение частоты за время X2d=2D/v составит
Af = yt = y^~. (1.72)
Измерив А/, можно вычислить искомое расстояние:
D-^-Д/. (1.73)
При непрерывном излучении вместо непрерывного линейного. изменения частоты практически приходится применять модуляцию по периодическому закону, т. е. периодически изменять частоту относительно некоторого исходного или среднего значения. Периодичность модуляции вносит некоторые особенности (ограничения), которые мы рассмотрим ниже.
Напомним, как в общем виде представляется ЧМ колебание. Если в излучаемом гармоническом колебании
Е = Ет cos (©/ + ф„) (1-74)
частота га изменяется по некоторому закону
© = ©(*), (1.75)
то модулированное по частоте колебание запишется в виде
£4M = Emcos^ + (1.76)
Подставляя в уравнение (1.76) выражение конкретного
закона изменения частоты га(7), можно получить развернутое
выражение для различных случаев модуляции. Например, при гармонической модуляции с частотой Q, т. е. когда
© (f) = ©о + Д© cos Qf, (1.77)
получаем
ЕЧ(Л = Ет cos ^©</ + А© | cos’fltdi + <p0J = Ет cos [©^ + 0 sin Ш — f ф0].
° (1.78)
где 0=Д©/й— так называемый индекс модуляции.
Для дальномерных целей может использоваться модуляция по синусоидальному, треугольному и пилообразному законам.
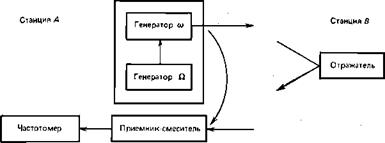
Общая блок-схема для реализации частотного метода изображена на рис. 10. На станции А имеется передатчик, содержащий генератор несущих колебаний и генератор модулирующего сигнала. Под воздействием последнего колебания модулируется по частоте по тому или иному закону, и, таким образом, передатчик излучает ЧМ колебания. В точке В, отстоящей от А на расстоянии D, установлен отражатель. Приемник-смеситель на станции А принимает как отраженное излучение, так и излучение непосредственно от передатчика. Эти два ЧМ сигнала смешиваются в приемнике, на выходе которого выделяется сигнал с частотой, равной разности частот смешиваемых колебаний. Его называют сигналом биений или преобразованным сигналом. Преобразованный сигнал подается на частотомер, измеряющий частоту биений.
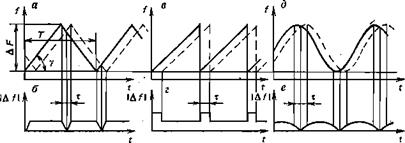
Рассмотрим работу такого устройства. Если ЧМ колебания распространяются на расстояние 2D, то независимо от закона изменения частоты кривая <a(t) в точке приема оказывается сдвинутой по времени относительно точки излучения на величину X2d=2D/v. Это показано графически на рис. 11 для различных видов модуляции — треугольной (а), пилообразной (в) и синусоидальной (д). Следовательно, в приемнике смешиваются два ЧМ колебания, частоты которых могут быть выра-
|
|
|
жены соответственно функциями <a(t) (прямой сигнал) и
«(*——— —(отраженный сигнал). Запишем смешиваемые
колебания в виде
|
^опорн — Ei COS 1 Li |
o)(t)dt + <p01l = Ey cos©,: D J |
(1.79) |
|
— t Eдиет — E2 COS 1 CD |
—— ^-^dt + Ф02 = £2 cos 02. |
(1.80) |
|
о |
При этом обычно амплитуда прямого сигнала намного превышает амплитуду отраженного сигнала, т. е. Еу^Еъ.
Как известно из радиотехники, для смешения сигналов необходимо подать их на нелинейный элемент. Нелинейность вольт-амперной характеристики смесителя приводит к наличию в выходном токе составляющей, пропорциональной произведе-
нию входных напряжений:
І = &£опорн-£дист = “ Е-уЕ^ COS (0і—0а) -|-
![]() f -^-£1£2cos(014-0a).
f -^-£1£2cos(014-0a).
Покажем, что первое слагаемое выражения (1.81) имеет частоту, равную в любой момент времени разности частот прямого и отраженного сигналов. Так как частота есть производная от фазы по времени, а фаза первого слагаемого равна (0Х — 02), для частоты получаем
![]()
![]()
![]()
![]() (1.82)
(1.82)
Поскольку частота физически не может быть отрицательной, формальный знак разностной частоты не имеет значения, и нас будет интересовать только абсолютная величина частоты биений.
Поведение частоты биений во времени при различных видах модуляции частоты излучения показано на рис. 11, б, г, е. Мы видим, что частота биений при синусоидальной ЧМ периодически меняется во времени по сложному нелинейному закону, а при треугольной и пилообразной формах ЧМ частота биений при данной задержке тго=2D/v постоянна во времени, за исключением небольших участков длительностью т, называемых зонами обращения. Влияние зон обращения тем меньше, чем меньше время т по сравнению с периодом модуляции Т. Постоянную частоту биений назовем основной и будем обозначать Afe-
Если не учитывать зоны обращения, то можно сказать, что при треугольной и пилообразной модуляции основная частота биений зависит только от величины задержки хю (т. е. от расстояния D). Эту зависимость нетрудно установить из следующих. соображений. Так как изменение частоты в рассматриваемых случаях совершается по периодически-линейному закону, можно использовать формулу (1.73), справедливую для линейного изменения частоты, а периодичность учесть в параметре у, выразив его через величины, характеризующие периодический процесс. Поскольку у —скорость изменения частоты df/dt, она выражается тангенсом угла наклона частотной прямой к оси времени. Из рис. 11, а, в видно, что в случае треугольной ЧМ
![]() (1.83)
(1.83)
а в случае пилообразной ЧМ
y = AFIT = AF-F, (1.84)
где AF—полоса качания частоты; F — частота модуляции. Подставляя эти выражения в уравнение (1.73), получаем: при треугольной модуляции
D = vAf6/4FAF (1.85)
при пилообразной модуляции
D = vAf6/2FAF. (1.86)
При синусоидальной модуляции частота биений Afc не только зависит от D, но и нелинейно изменяется внутри каждого полупериода модуляции. Однако и в этом случае можно получить зависимость только от D, исключив указанную нелинейность, если рассматривать среднее за полупериод модуляции значение частоты биений, т. е. величину
А/б = —zr ТI Af6(t) | dt. (1.87)
і о
Как показывают вычисления, выражение (1.87) при гармоническом законе модуляции дает результат, совпадающий с формулой (1.85).
Измерение частоты биений. Ошибка дискретности. Частота биений измеряется при помощи частотомера, подсчитывающего среднее значение частоты Д/б — Обычно применяются частотомеры, работающие по принципу счета числа импульсов. Преобразованный сигнал частоты Д/д подвергается ограничению и дифференцированию, после чего полученными импульсами запускается формирователь, вырабатывающий стандартные импульсы постоянной амплитуды, длительности и формы, поступающие на счетчик импульсов.
При таком методе измерения частоты биений возникает так называемая постоянная ошибка, или ошибка дискретности. Дело в том, что при времени измерения, существенно превышающем период модуляции частоты, т. е. когда при измерении четко выражена периодичность модуляции, спектр преобразованного сигнала состоит из дискретных составляющих, отстоящих друг от друга на интервал, равный частоте модуляции F. Поэтому при изменении расстояния то минимальное изменение частоты биений, которое может быть зафиксировано счетчиком в виде изменения числа импульсов на единицу, равно bf=F. А это означает, что минимальное изменение расстояния, которое способен зарегистрировать прибор, составляет в соответствии с уравнением (1.85) или (1.86)
8D = i>6f/pFAF = vFlpFAF = v/pAF, (1.88)
где р = 4 для треугольной и синусоидальной модуляции и р = 2 для пилообразной модуляции.
Так как подсчитываемое число импульсов может быть только целым числом, расстояние может быть измерено с точностью до величины 6D. Величина бD называется постоянной ошибкой потому, что она не зависит от измеряемой дальности. Из формулы (1.88) следует, что прямой путь уменьшения постоянной ошибки заключается в увеличении размаха модуляции AF, т. е. девиации частоты (девиация равна AF/2). Однако практические возможности этого способа довольно ограниченны. При несущей порядка нескольких гигагерц можно достичь величины AF порядка сотни мегагерц. Если AF= = 100 МГц, то ошибка бD при р = 4 составит 0,75 м.
Для исключения постоянной ошибки применяют более сложные методы построения схем дальномера.
Условие однозначности измерения расстояния. Для того чтобы расстояние могло быть измерено однозначно, время задержки отраженного сигнала должно быть меньше половины периода модуляции частоты: т<7’/2, т. е. 2D/v<l/F. Отсюда следует, что максимальное однозначно измеряемое расстояние при заданной частоте модуляции F
Dmtx = v/4F (1.89)
и соответственно обеспечивающая такую дальность действия частота должна выбираться из условия
Pmax ^ W,4Dmax — (1.90)
Практически частоту Fm&x выбирают намного меньше, чем у/4/)тах.- Это обусловлено тем, что при увеличении частоты, т. е. при уменьшении периода модуляции, начинают играть заметную роль зоны обращения, влиянием которых можно пренебрегать лишь при т<СТ72. В этом случае формулы (1.85) и (1.86), полученные без учета зон обращения, становятся некорректными, так как зависимость средней частоты биений от расстояния получается нелинейной, что усложняет калибровку шкалы частотомера и обработку преобразованного сигнала.
О точности частотного метода. Дифференцируя формулы (1.85) и (1.86) и переход к средним квадратическим ошибкам, получим:
т. е. относительная ошибка измерения дистанции обусловлена: нестабильностью частоты модуляции m^fF, нестабильностью полосы качания или девиации частоты m&F/AF, относительной ошибкой измерения частоты биений яід^/А/б и относительной ошибкой определения скорости распространения сигнала mv/v. Точность приборов, реализующих частотный метод, обычно имеет порядок 10-3 (это определяется назначением прибора, а не принципиальными ограничениями).
О применении частотного метода. Случай, когда отражатель неподвижен, был рассмотрен с целью изложения основ частотного метода измерения дальности. Практически же частотный метод применяется главным образом в самолетных радиовысотомерах малых высот и в некоторых радиолокационных системах. В этом случае из-за движения прибора или цели (отражателя) возникает дополнительное изменение частоты вследствие эффекта Доплера и частота биений становится равна сумме дальномерного и доплеровского приращений частоты:
+ = (1.92)
где f (t) — модулированная частота излучения передатчика, VD — радиальная составляющая скорости (проекция модуля вектора скорости на направление передатчик — отражатель); знак перед-последним членом зависит от направления движения.
Это усложняет обработку сигнала для получения информации о дальности, но в то же время дает возможность определения скорости движущегося объекта по доплеровскому сдвигу частоты. Доплеровские системы геодезического назначения рассматриваются в § 22.