 ДАЛЬНОСТЬ ДЕЙСТВИЯ И ТОЧНОСТЬ ФАЗОВЫХ СВЕТОДАЛЬНОМЕРОВ
ДАЛЬНОСТЬ ДЕЙСТВИЯ И ТОЧНОСТЬ ФАЗОВЫХ СВЕТОДАЛЬНОМЕРОВ
.Дальность действия. Как отмечалось в § 1 (стр. 18), оптическое излучение может распространяться только в пределах прямой видимости. В этих пределах реальное максимальное расстояние, которое можно, измерить светодальномером, зависит от дальности действия прибора. Дальность действия определяется как расстояние, после двукратного пробега которого (до отражателя и обратно) мощность принимаемого сигнала становится равной минимально допустимому (пороговому) значению, т. е. значению, при котором еще возможно измерение разности фаз с требуемой точностью. Дальность действия зависит от параметров аппаратуры и прозрачности атмосферы. .
В § 14 приводилась формула для дальности действия импульсных дальномеров класса «Земля—космос» [формула
(3.20) ]. Дальность действия Dm&x для светодальноме{юв с непрерывным излучением, в частности фазовых, может быть оценена по той же формуле, если в ней энергию Е заменить на мощность излучения Р, а спектральный коэффициент прозрачности о отнести не ко всей толще атмосферы, а к слою протяженностью Дтах» т. е. заменить ов на о2*».*:
Здесь Р — мощность излучения источника; Рт in — минимально допустимая мощность на приемнике, или, что то же, пороговая чувствительность приемника по мощности. Р и Ртm выражаются в ваттах. Остальные обозначения те же, что и в формуле (3.20).
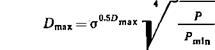 |
||
Выражение (3.53) можно представить в, более удобном для практического использования виде, если перейти от площадей S к диаметрам d и от телесных углов Q к плоским углам а. Воспользовавшись соотношениями S = ztd2/4 и Q=jta2/4, получим
где dorp и <2Пр — диаметры отражателя и приемной оптической системы; оспер и а0тр — плоские углы расходимости излучения, выходящего из передатчика и отраженного отражателем.
Потери света в оптических системах зависят от количества оптических деталей и их прозрачности (включая модуляторы света, оптические фильтры и т. п.). Обычно общий оптический коэффициент пропускания тіопт=т)пер’ПотрТ]пр составляет величину порядка нескольких сотых.
Атмосферное затухание при достаточно длинных трассах или плохой видимости (малой прозрачности атмосферы) может привести к очень большим потерям света. Так, при хорошей видимости, соответствующей коэффициенту прозрачности о=0,9 (затухание ~0,5 дБ/км), при длине трассы 20 км получаем о2о=0,014, а при средней видимости, соответствующей о=0,8 (затухание ~ 1 дБ/км), величина о2г> на той же дистанции уменьшается до 0,0001.
В уравнении. дальности действия (3.54) неизвестная величина Ьшах содержится в обеих частях равенства. В другом виде его представить не удается. Такие уравнения в алгебре называются трансцендентными и решаются, в сущности, методом подбора. Пороговая чувствительность определяется заданной ошибкой измерения и способом регистрации сигнала и может быть в принципе рассчитана с достаточной точностью для каждой конкретной дальномерной системы. Обычно уравнение дальности представляют в виде кривой зависимости Dmах от о, выражающей дальность действия при различных состояниях атмосферы.
Пути увеличения дальности действия следуют из анализа рассмотренных формул. Это увеличение мощности излучения (или яркости) источника, увеличение диаметров оптических систем, уменьшение Рты и т. д. Однако далеко не все эти пути
приемлемы или легко осуществимы. Наиболее эффективными средствами можно считать использование лазеров [20], а также разработку дальномерных систем с активным отражателем, имеющим собственный источник излучения [13, 15, 19].
Применение лазеров в качестве источников излучения позволяет, кроме общего увеличения дальности действия из-за большей интенсивности излучения, резко повысить дальность действия светодальномера в светлую часть суток за счет монохроматичности излучения лазера путем постановки в приемной оптической системе узкополосного оптического фильтра, пропускающего сигнал и подавляющего фон (см. § 13, стр. 135—136).
Из существующих светодальномеров наибольшей дальностью действия (около 80 км) обладает американский лазерный дальномер Теодолит 3G (см. табл. 4).
Точность светодальномерных измерений. Исходя из общей формулы (1.68) для точности фазовых дальномеров можно сделать применительно к светодальномерам следующие выводы.
Ошибка измерения разности фаз тф зависит от многих факторов, связанных с конкретно используемым способом фазовых измерений. Для современных светодальномеров она обычно лежит в пределах 0,14-1° и носит в основном случайный характер. Ее линейный эквивалент, т. е. ошибка в расстоянии, обусловленная ошибкой тф (величина —v— тф =
в формуле (1.68)), в соответствии со сказанным на стр. 159 может составлять при аналоговом методе измерений Я/3000, а при цифровом Х/5000 или даже Я/Ю000. При частоте 15 МГц (Я,=20′ м) это дает погрешность примерно 2—3 Мм.
Ошибка постоянной поправки тк зависит от конструкции прибора, его точности и способа определения поправки и имеет, как правило, систематический характер. Эта ошибка в современных приборах меньше 5 мм, а в отдельных случаях (высокоточные приборы с синхронной демодуляцией, принудительное центрирование при определении поправки) она составляет доли миллиметра.
‘ Совместное влияние всех ошибок, не зависящих от величины расстояния, обычно дает, таким образом, результирующую погрешность 3—5 мм.
Поскольку значение скорости света в вакууме с= = 299792458 м/с известно сейчас со средней квадратической погрешностью 1,2 м/с, т. е. с относительной ошибкой 4 • 10~9, этой составляющей общей погрешности можно пренебречь. В пропорциональной расстоянию части общей ошибки существенными оказываются, таким образом, погрешность частоты модуляции и погрешность фактического значения показателя преломления воздуха.
Для приборов большой дальности действия необходима стабильность частоты от (1—2) • 10-7 до 10-6. Такая стабильность может быть достигнута лишь при использовании термостатированных кварцевых резонаторов.
Погрешность знания показателя преломления воздуха зависит от ошибок определения метеорологических элементов — температуры, давления и влажности воздуха. Теоретически величину показателя преломления можно определить с точностью 10~7, но практически такая точность может быть достигнута только применением дисперсионного метода определения показателя преломления, т. е. в двухволновых светодальномерах.
Пользуясь формулой (2.25) из § 8 (стр. 74) и приведенными там же значениями производных, можно записать, что ошибка в расстоянии, обусловленная ошибками метеоэлементов, а также ошибкой знания эффективной длины волны излучения Шх (ее называют дисперсионной ошибкой), составит
(mD)x. r. P.e = D — КГ» V(0,04)V + (1,0fm + (0,4)2 tn% + (0,05)2m .
‘ (3.55)
I /Wn і t p «
Относительная ошибка —— D ‘ ‘— равна ошибке показателя преломления тп1п^тп.
Для современных (лазерных) дальномеров дисперсионную ошибку т% можно принять равной нулю. Что касается ошибок метеоэлементов, фигурирующих в приведенной формуле, то здесь важно подчеркнуть, что они выражают собой ошибки, с которыми нам известны «истинные» — средние вдоль трассы (среднеинтегральные) значения температуры, давления и влажности, т. е. величины <Т>, <Р> и <е>. Каждая из ошибок mr, trip и те складываются из двух компонентов: так называемой ошибки представительства и ошибки собственно измерения данного метеорологического элемента.
Так как метеоэлементы измеряются обычно лишь на концах линии (а иногда и только на одном ее конце), то ошибка представительства выражает собой ту погрешность, с которой осредненное только по двум крайним точкам значение метеоэлемента будет представлять его «истинное» — среднеинтегральное — значение. Значения ошибок представительства зависят от длины трассы, ее характера и конкретных атмосферных условий и в среднем могут быть охарактеризованы такими величинами: 0,7° для температуры, 0,7 мм рт. ст. для давления и 0,8 мм рт. ст. для влажности.
Второй компонент — ошибки собственно измерений метеоэлементов (в дискретных точках), выполняемых обычно при
помощи барометра-анероида (давление) и аспирационного психрометра (температура и влажность). В среднем значения этих ошибок можно принять равными 0,2° для температуры, 0,3 мм рт. ст. для давления и 0,5 мм рт. ст. для влажности. Некоторые дополнительные погрешности могут вызываться влиянием временных изменений измеряемых метеоэлементов, однако они могут быть значительно ослаблены выполнением метеоизмерений через достаточно небольшие промежутки времени с осреднением результатов (частота измерений устанавливается эмпирически, сообразуясь с условиями погоды, временем суток и т. п.; практически в большинстве случаев достаточно повторять измерения каждые 15 мин, а при необходимости особо точного контроля, например при исследовательских работах, возможно применение метеоприборов с непрерывной регистрацией). Полезно запомнить, что ошибка в температуре на 1° дает ошибку в показателе преломления, а следовательно, и в расстоянии, равную 1 • 10-6, ошибка в давлении на 1 мм рт. ст.— 4* 10~7, а ошибка во влажности на 1 мм рт. ст.— 5 • 10-8; эти цифры есть не что иное, как значения производных в формуле для общей ошибки.
Таким образом, каждую из ошибок тт, тР и те можно для оценочных расчетов представить в виде
ffl метео = Шпредст "Ь ^изм, (3.56)
где Шпредст — ошибка представительства; тизм — ошибка измерения метеоэлемента. Если мы учтем это соотношение в формуле (3.55) и затем подставим приведенные выше численные значения для всех составляющих ошибок, то для относительной ошибки расстояния (mD)T, p,e/D или, что то же, для тп получим величину 0,9 «10і6. Отметим, что в менее благоприятных условиях, чем те, для которых были приведены численные значения ошибок, ошибка т<я> увеличивается до (2—3) • 10-6.
Если учесть все источники ошибок и принять во внимание повышение инструментальной точности за счет многократных измерений, то результирующая ошибка измерения расстояний светодальномерами, выраженная уравнением вида (1.71) (§ 4), составит для большинства приборов
mD = ±[(3-т-10) мм + (1-т-10) мм/км]. (3.57)
Разумеется, эта оценка относится только к одноволновым светодальномерам. Сведения о точности двухволновых светодальномеров приведены при их описании в § 15.