Бурение грунтовых зондов, установка энергетических колодцев

Радиогеодезические системы, в отличие от радиодальноме­ров, осуществляют измерения до подвижного объекта. При этом возможны различные варианты осуществления измерений.

Первый вариант дает возможность получить расстояние между неподвижной точкой А с известными координатами и движущейся точкой Р (рис. 86, а) или приращение этого рас­стояния. Второй вариант дает возможность получить разность расстояний между движущейся точкой Р и неподвижными точ­ками Л и В с известными координатами (рис. 86, б) или при­ращение ^той разности расстояний.

Непосредственно расстояние АР в первом варианте или раз­ность расстояний АР — ВР во втором варианте можно получить при помощи временных (импульсных), фазово-временных или многочастотных фазовых РГС. Под многочастотными понима­ются системы, каждая станция которых может работать на не­скольких рабочих частотах, обеспечивающих разрешение много­значности фазовых измерений. О таких системах говорят, что они работают в дальномерном режиме. Наряду с этим большое распространение получили так называемые одночастотные фа­зовые системы, в которых каждая из станций может работать только на одной определенной («своей») рабочей частоте, так что частоты всех станций системы образуют один рабочий комплект частот, в отличие от многочастотных систем, где та­ких комплектов несколько. Одночастотные РГС непосредст­венно измеряют лишь приращения линейных величин (см.

ниже); в этом случае многознач­ность разрешается с использова­нием непосредственного счета фазо­вых циклов при перемещении под­вижной станции. Если такая система реализована в первом варианте (рис. 86, а), ее называют работаю­щей в режиме радиолага, а если во втором варианте (рис. 86, б) — ра­ботающей в режиме фазового зон­да. Соответственно и способы раз­решения многозначности в этих слу­чаях именуют способом радиолага и способом фазового зонда.

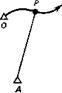
При способе радиолага одна из станций, например, распо­ложенная на подвижном объекте Р, излучает радиоволны и принимает их после отражения (точнее, ретрансляции) от не­подвижной станции А. При движении объекта Р индикатор под­вижной станции непрерывно фиксирует изменение разности фаз между излучаемыми и отраженными сигналами. Следова­тельно, при способе радиолага измеряется лишь изменение (приращение) расстояния между станциями, а не само это расстояние. Чтобы иметь возможность определять по этим дан­ным расстояние между станциями в любой момент времени, надо, очевидно, заранее знать исходное расстояние АО, т. е. расстояние между станциями в момент нахождения подвижной станции в начальной точке О маршрута ее движения. Другими словами, исходная точка маршрута должна быть геодезически привязана.

При способе фазового зонда суть дела сводится к следую­щему. Неподвижные станции А я В излучают колебания раз­ных частот. При этом частоты станций могут быть либо жестко связаны друг с другом, когда частота одной станции зависит от частоты другой станции (когерентный вариант), либо совер­шенно независимы, автономны (некогерентный вариант). При­емная станция в точке Р, называемая собственно фазовым зон­дом, принимает излучение обеих неподвижных станций. (В не­когерентном варианте требуется дополнительная неподвижная станция для создания опорного сигнала разностной частоты, передаваемого на фазовый зонд, но сейчас это для нас несуще­ственно.) При движении фазового зонда его индикатор непре­рывно фиксирует изменение разности фаз между сигналами, пришедшими от станций А и В. Следовательно, при этом спо­собе измеряется изменение (приращение) разности расстояний от зонда до каждой из неподвижных станций. Чтобы опреде­лить саму разность расстояний АР — ВР, необходимо заранее знать исходную разность расстояний АО — ВО, т. е., как и при способе радиолага, требуется геодезическая привязка началь­ной точки О маршрута движения фазового зонда.

Рассмотрим теперь, как решается задача определения по­ложения точки Р.

На рис. 86, а расстояние АР определяет окружность с цент­ром в точке А, проходящую через Р, являясь радиусом этой окружности, а на рис. 86, б разность расстояний АР—ВР, как известно из аналитической геометрии, определяет ветвь гипер­болы с фокусами в точках А и В, проходящую через Р. Таким образом, полученная величина (расстояние или разность рас­стояний) дает нам одну изолинию — окружность или гиперболу, на которой находится искомая точка Р. Чтобы однозначно определить эту точку, надо иметь возможность построить вто­рую аналогичную изолинию, пересекающую первую в этой точке. Для этого нужно в обоих случаях ввести еще одну не­подвижную станцию с известными координатами, что позволит определить второе расстояние (от этой станции до точки Р) на рис. 86, а и, следовательно, вторую окружность, или соот­ветственно вторую разность расстояний на рис. 86, б и, следо­вательно, вторую гиперболу. Практически именно так и посту­пают, и в зависимости от вида изолиний называют систему кру­говой или гиперболической [31].

Круговые системы. Полная геометрия круговой системы с сеткой изолиний изображена на рис. 87. Система состоит из двух неподвижных станций Л и б с известными координатами, называемых базисными, и подвижной станции, перемещаю­щейся по некоторому маршруту из начальной точки О. Пусть в некоторый момент станция находится в точке Р, положение которой надо определить. Если система позволяет измерять сами расстояния, то непосредственно находятся величины грл и грв. Если же система работает в режиме радиолага, то дол­жны быть известны начальные расстояния г°п и г°в. Тогда при перемещении подвижной станции из точки О (г°а, г°в) в опре­деляемую точку Р (грл, грв) будут измерены приращения рас­стояний

brA=rPA~rA>

&rB = rB — Т°В‘

и, следовательно, искомые расстояния можно получить из со­отношений

ГРа=Га + Ага г В = ‘г В + Кг в.

Определение координат точки Р по известным координатам точек А и В и двум измеренным расстояниям г а и гв рассмат­ривается в § 25.

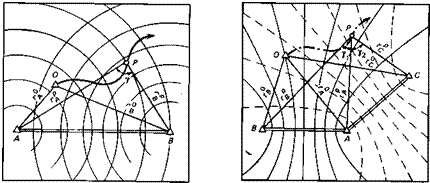
Гиперболические системы. Геометрия гиперболической си­стемы показана на рис. 88. В пунктах А, В и С с известными координатами располагаются неподвижные базисные стан­ции— центральная станция А и боковые станции В и С, а подвижная станция перемещается по некоторому маршруту из начальной точки О. На базисе АВ строится одно семейство гипербол с фокусами в точках А и В, а на базисе АС — второе семейство гипербол с фокусами в точках А и С. Маршрут под­вижной станции располагается в зоне перекрытия обоих се­мейств гипербол. Пара станций А и В образует с подвижной станцией один канал системы, а пара станций А и С образует с подвижной станцией другой канал. Пусть в некоторый мо­мент подвижная станция находится в точке Р, положение ко­торой надо определить. Если система позволяет получать сами разности расстояний (например, имеется необходимая сетка рабочих частот для разрешения неоднозначности), то непосред­ственно находятся величины грА — грв и гра — грс — разности расстояний по обоим каналам, называемые гиперболическими координатами. Если же система работает в одночастотном режиме фазового зонда, то должны быть известны начальные разности расстояний г°а — г°в и г°А — г°с (гиперболические координаты начальной точки О). Тогда при перемещении под­вижной станции из точки О в точку Р будут измерены прира­щения этих разностей расстояний:

по’ каналу базиса А В АгЛВ = (г%—г%) — (г°А—гв),

по каналу базиса АС АгАС = {г% — гс)—{г°А — г°с), .

и, следовательно, разности расстояний в точке Р, т. е. ее гипер­болические координаты, находятся из соотношений

ТРА — Тв = {г°А — Гв) + А/ДВ»

fjl — г С = {г А —r°c) + АС-

Далее решается задача: найти координаты точки Р (в какой — либо общепринятой системе координат) по известным коорди­натам трех базисных станций и двум измеренным разностям расстояний. Эту задачу часто называют задачей фазового зонда. Она рассматривается в § 25.

Комментарии запрещены.