Магнитооптические модуляторы
Магнитооптические модуляторы
В некоторых материалах, помещенных в магнитное поле, наблюдается изменение показателя преломления при прохождении через такую среду электромагнитной волны с круговой
поляризацией, причем знак приращения показателя преломления зависит как от направления магнитного поля относительно направления распространения проходящей через среду волны, так и от знака круговой поляризации (последняя может быть «правой» или «левой» в зависимости от того, в какую сторону вращается вектор электрического поля волны). Этот эффект получил название магнитооптического эффекта Фарадея. Величина приращения показателя преломления линейно зависит от напряженности магнитного поля
д п==_!_ауя, (з. п)
4я
где X — длина волны проходящего через среду излучения; Л — напряженность приложенного магнитного поля; V — постоянная, которая зависит от свойств данной среды и называется постоянной Верде.
Очевидно, что при изменении напряженности магнитного поля Н по какому-либо закону фаза прошедшей через среду оптической волны окажется модулированной по тому же закону, причем приобретенный оптической волной дополнительный сдвиг фазы связан с напряженностью магнитного поля соотношением
Дф = ±-VlH, (3.12)
где I — длина пути излучения в среде, помещенной в магнитное поле, вектор напряженности которого коллинеарен вектору направления распространения оптической волны.
Нетрудно показать, что волна с линейной поляризацией может быть представлена в виде суммы двух волн с круговой поляризацией, имеющих одинаковые амплитуды и частоты колебаний, но противоположные направления вращения вектора электрического поля. При прохождении линейно поляризованной волны через среду, обладающую эффектом Фарадея, составляющие с правой и левой круговой поляризацией приобретут одинаковые по величине, но различные по знаку сдвиги фаз, и суммирование их на выходе из среды даст линейную поляризацию, повернутую относительно исходной на угол
0 = 2Дф = VIH. (3.13)
Таким образом, для волны с линейной поляризацией изменение напряженности магнитного поля приведет к поляризационной модуляции прошедшего через среду излучения (повороту плоскости поляризации волны на угол, зависящий от Я).
Установив на пути такого поляризационно-модулированного излучения анализатор, можно получить амплитудную модуляцию, поскольку в соответствии с законом Малюса при прохождении линейно поляризованной волны через анализатор интен-
|
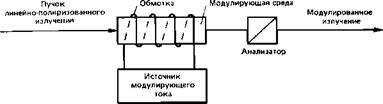
Рис. 38. Схема амплитудного модулятора на основе эффекта Фарадея |
сивность излучения на выходе пропорциональна cos2a, где a — угол между плоскостью пропускания анализатора и плоскостью поляризации падающей волны.
Схема амплитудного модулятора на основе эффекта Фарадея изображена на рис. 38. Магнитное поле налагается на среду путем помещения последней внутри катушки (соленоида), через которую пропускается электрический ток. Напряженность магнитного поля внутри соленоида пропорциональна силе тока и числу витков, приходящемуся на единицу осевой длины соленоида. Поэтому модуляция производится в данном случае путем изменения силы тока (а не напряжения U, как это имеет место в электрооптических модуляторах).
Модуляционная характеристика амплитудного магнитооптического модулятора качественно аналогична характеристике модулятора на основе линейного электрооптичёского эффекта, с той лишь разницей, что по оси абсцисс откладывается сила тока, а не напряжение. Величина полуволновой силы тока /хд имеет в данном случае тот же физический смысл, что и полуволновое напряжение U/2 в электрооптических модуляторах.
Эффектом Фарадея обладают многие оптически прозрачные среды, в том числе обычные Стекла. Однако величина постоянной Верде для большинства материалов мала и для глубокой модуляции излучения требуются очень сильные (импульсные) магнитные поля. Магнитооптические модуляторы иногда применяются для модуляции добротности резонатора в мощных твердотельных лазерах, которые работают с невысокой частотой повторения излучаемых импульсов.