Бурение грунтовых зондов, установка энергетических колодцев

В равнинных районах свето — и радиодальномерами обычно измеряют линии, имеющие не слишком большой угол наклона. Однако в горных районах часто требуется измерять линии со
значительными углами наклона к горизонту. При измерениях же радиогеодезическими системами, в которых подвижная стан­ция находится на самолете, случай значительного угла наклона является доминирующим.

При наклонной трассе наблюдается некоторая закономер­ность распределения показателя преломления вдоль трассы, обусловленная тем, что плотность воздуха, а значит, и его по­казатель преломления, убывает с высотой. Следовательно, в этом случае имеется некоторая дополнительная информация о распределении п вдоль трассы, которую можно использовать для определения среднеинтегрального показателя преломления.

В этом случае выражение (2.34) для среднеинтегрального показателя преломления можно представить в виде

(п) =-J — f п [Н (*)] dx, (2.50)

D о

где п[Н(х)] — текущий показатель преломления, зависящий от высоты Я, которая, в свою очередь, является функцией преж­ней переменной — текущего расстояния х. Зависимость же п[Н(х)], или, проще, п(Н), обычно дается выражением вида п(Н) =«н0/(Я), где пн0 —показатель преломления на некото­рой исходной высоте Н0, для определения которого в реальных условиях нужно измерить метеорологические элементы на этой высоте. Таким образом, получаем метод определения средне­интегрального показателя преломления, при котором метеоро­логическую информацию достаточно иметь только в одной на­чальной точке линии, а вместо метеорологических измерений в других точках линии применяется некоторый определенный закон изменения п с высотой.

Разумеется, этот способ является, по существу, также при­ближенным, и степень этой приближенности будет опреде­ляться отличием реального распределения п по высоте от при­нятого нами закона.

Принятие какого-либо закона изменения показателя пре­ломления (или, что физически эквивалентно, температуры, дав­ления и влажности) с высотой приводит к созданию той или иной модели атмосферы. Такую модель называют стандартной атмосферой. ~

Стандартная атмосфера. Существует несколько различным образом построенных стандартных атмосфер. В метеорологии не интересуются специально показателем преломления для электромагнитных волн и стандартная атмосфера дается в виде зависимостей температуры, давления и влажности от высоты:

Т(Н)= ThJt(H)]

Р (Н) = PHjp (ну,

e(H)=eHj,№

За исходные значения THq, PHq и еНо могут быть приняты вполне определенные значения, отвечающие средним условиям на высоте Н0, а функции f задаются в соответствии с обобщен­ными экспериментальными данными.

В радиометеорологии атмосфера изучается применительно к распространению электромагнитных волн и стандартная ат­мосфера задается моделью поведения обобщенной характери­стики— показателя или индекса преломления, а не отдельных метеоэлементов, что, конечно, более удобно для радиогеодези­ческих целей.

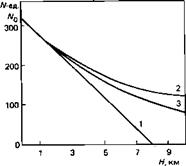
Пересчет стандартных атмосфер, заданных через метеоэле­менты, на модели распределения показателя преломления об­наружил довольно значительные отклонения этих моделей от среднего распределения показателя преломления в реальной атмосфере. Зависимость индекса преломления от высоты полу­чается в этих моделях либо линейной (модель с постоянным градиентом dNjdH), либо параболической. Линейная модель является простейшей; в ней принимается dN/dH=—40ІУ-ед/км (для радиоволн) и индекс преломления N(H) уже на высоте 8 км обращается в нуль (как в вакууме), что не соответствует действительности. Поэтому линейная зависимость является до­вольно грубым приближением. Точность параболической мо­дели часто также недостаточна;

Экспериментальные исследования показали, что более точ­ной является экспоненциальная модель атмосферы, в которой вертикальная стратификация (распределение) индекса прелом­ления дается выражением вида

N(H) = NHoexp[-q(H~H0)]. (2.51)

Коэффициент q обычно лежит в пределах 0,10—0,25; на­пример, для территории СССР он может изменяться от 0,11 до 0,19.

Экспоненциальная модель была рекомендована в 1959 г. в качестве международной.

На рис. 18 показаны для сравнения кривые зависимостей N (Н) для линейной, параболической и экспоненциальной мо­делей атмосферы.

Биэкспоненциальная модель. Простая экспоненциальная модель, описываемая выражением (2.51), достаточно хорошо характеризует структуру усредненного показателя преломления в пределах первых нескольких километров над земной поверх­ностью. Бин и Даттон (США) на основании анализа большого статистического материала показали [3], что для большего диапазона высот лучшие результаты в смысле приближения к реальным стратификациям дает так называемая биэкспо­ненциальная модель, построенная на раздельном учете сухой и влажной составляющих индекса преломления. В этой модели
зависимость N от Н дается вы­ражением вида

N (Н) = Nc (Н) + NB (Я) = Nc X

ехр (_^) + л,’ехр(__?г)’

(2.52)

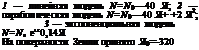где N с и — значения сухой и влажной составляющих на по­верхности Земли; Нс и #в — так называемые масштабы высот для этих составляющих. Масштабы высот представляют собой вы­соту, на которой значение со­ответствующей составляющей уменьшается в е=2,718 раз по сравнению с ее значением на по­верхности Земли. Для террито­рии Европы и большей части Азии можно принять Нс = 9,4 км; Яв=2,6 км [3].

Значения сухой и влажной составляющих на поверхности Земли определяются для радиоволн по формуле (2.27):

где ТНо, РИй и eHf) — температура, давление и влажность воз­духа на поверхности Земли. Коэффициенты а, b и с берутся из табл. 2 (например, по Фруму и Эссену). ч

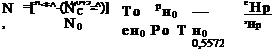Для световых волн значения Nc и ЛГВ можно определить по формуле Баррелла и Сирса:

Таким образом, биэкспоненциальную модель атмосферы можно считать наиболее совершенной, что дает основание ее рекомендовать при определении среднеинтегрального показа­теля преломления на наклонных трассах. Для определения <Я> в биэкспоненциальной модели надо подставить (2.52) в общее выражение (2.50): .

о о

Для практических вычислений используют приближенный метод — разбиение атмосферы на сферические концентрические слои равной толщины АН с предположением о постоянстве градиента индекса преломления в каждом слое. Тем самым ин­тегралы в уравнении (2.57) заменяются суммами. Если трасса электромагнитной волны пересекает k слоев, то суммы будут состоять из k членов и задача сводится к численному интегри­рованию методом суммирования. При этом точность определе­ния <N> будет тем выше,, чем меньше взят интервал АН по высоте. Из-за уменьшения АН возрастает число слоев k, т. е. число членов суммы, что значительно увеличивает объем вы­числений, поэтому такого рода вычисления целесообразно вы­полнять на ЭВМ.

Комментарии запрещены.