 Преобразование электромагнитных колебаний
Преобразование электромагнитных колебаний
Модуляция. Изменение параметров колебания во времени по определенному закону называется модуляцией, а устройства, его осуществляющие,— модуляторами. В соответствии с видом модулируемого параметра (А, © или <р0) различают амплитудную (AM), частотную (ЧМ) и фазовую (ФМ) модуляции. Закон изменения параметра в простейшем случае может быть гармоническим. При этом модулируемый параметр Р представляется в виде
P(t) = P0+APcosQf = Р0(1 +mcosQt), (1.12)
где Ро — соответствующий параметр немодулированного колебания, ДР — амплитуда изменения параметра, й=2пР — круговая частота модуляции (F — частота модуляции). Величину т=АР/Ро называют коэффициентом модуляции.
Модуляцию по прямоугольному закону часто называют манипуляцией. Так как при изменении частоты меняется фаза колебания и наоборот, ЧМ и ФМ неразрывно связаны друг с другом. Иногда их объединяют под названием «угловая модуляция».
Частоту модулируемого колебания f=©/2n называют несущей частотой, а само колебание — несущим колебанием. При этом обычно f^>F (соответственно ©>•&).
При модуляции света часто применяют еще один вид модуляции— поляризационную, при которой изменению подвергается состояние поляризации света.
Модуляция по гармоническому закону наиболее часто применяется в дальномерных устройствах. Пусть немодулированное колебание имеет вид
S = Л0 cos (©о/ + фо)- (1.13)
При гармонической амплитудной модуляции в соответствии с (1.12) амплитуда меняется во времени по закону
A (t) = A0+АА cosQ/ = A0(l — f mcosQf), (1.14)
и уравнение AM колебания будет
Sam = A0(1-t-mcosQ/)cos(©/-l-<Po)» (1.15)
где т=АА/А0 называется коэффициентом амплитудной модуляции.
При гармонической частотной модуляции имеем
со {t) = tt>o + A© cos ffl. (1.16)
Если частота — функция времени, то в уравнении (1.13) вместо coot мы обязаны записать.[©(*)*# и, следовательно,
S4M = А0 cos (со0 + Л © cos Q<) dt + <р0 j =
= ^0cos(©of + PsinQf + q)0), (1.17)
где величина p = A©/Q называется индексом частотной модуляции, а А© — девиацией частоты.
При гармонической фазовой модуляции вместо начальной фазы ф0 в уравнении (1.13) мы должны записать
ф’(0 = фо + Лф cos Qf, (1.18)
а следовательно,
5фМ = /40cos(©o< + A«pcosQ/ + cpo), (1.19)
где Дер есть максимальное отклонение фазы от среднего значения (девиация фазы). Девиацию фазы также называют индексом фазовой модуляции.
Из сравнения уравнений (1.17) и (1.19) видна общность частотной и фазовой модуляций. Поэтому ФМ колебание можно рассматривать как ЧМ колебание, в котором, однако, частота изменяется в соответствии не с модулирующим колебанием, а с его производной по времени. Точно так же ЧМ колебание можно рассматривать как ФМ колебание, в котором фаза изменяется в соответствии не с модулирующим колебанием, а с его интегралом по времени.
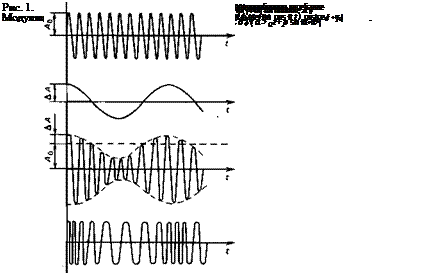
На рис. 1 показаны формы AM и ЧМ колебаний при модуляции по гармоническому закону.
Демодуляция. Демодуляцией или детектированием в радиотехнике называется такой процесс, в результате которого из сложного модулированного колебания выделяется (восстанавливается) модулирующее колебание. Соответствующие устройства называются демодуляторами или детекторами. Различают детекторы AM, ЧМ и ФМ колебаний. При этом, детектирование ЧМ и ФМ колебаний наиболее просто осуществляется путем преобразования их в AM колебание, которое затем детектируется. Детектирование AM колебания представляет собой нелинейную операцию, в процессе которой происходит перемножение этого колебания
$ам = Л0(1 — f mcos£M)cos©0f
либо на колебание несущей частоты SH=A0 cos ©0/, либо само на себя (квадратичное детектирование). В результате перемножения получается сумма слагаемых (спектр), одно из ко-
Смодулированное (несущее) колебание А0 cos(o>0t+f0)
 |
торых будет иметь модулирующую частоту Q. Например, в первом случае получаем
тд2 д2
5ам5и= -£- + —^-cosQ^H—^-(1+mcosQ/)cos2cO(/.
(1.20)
Второй член этого выражения есть искомое колебание модулирующей частоты Q, которое можно выделить при помощи соответствующих фильтров.
Детектирование, описываемое выражением вида (1.20), носит название’ синхронного детектирования (т. е. детектирования, при котором перемножаемые сигналы имеют одинаковую частоту). На синхронном детектировании основана работа фазовых детекторов, используемых в дальномерах.
Гетеродинирование. Гетеродинированием называют взаимодействие (смешение) колебаний двух (или более) различных частот. Это взаимодействие может представлять собой перемножение или более сложную операцию, определяемую видом характеристики смесителя. Гетеродинирование используется для преобразования, в частности понижения частоты колебаний. Если на смеситель поступают сигнал
S = A cos(©/ + q>o)
и сигнал от гетеродина (вспомогательного генератора)
Sr = B cos (ю, і + фг),
то на выходе смесителя образуется совокупность (спектр) колебаний различных комбинационных частот,- среди которых имеются колебания разностной частоты Q = | со — (ог| вида
s = C cos [Ш— (фо—фг)]. (1.21)
Эти колебания можно выделить при помощи фильтра, настроенного на разностную частоту Q. Таким образом, происходит понижение частоты сигнала со до значения Q. При этом фаза колебания разностной частоты равна разности фаз смешиваемых колебаний.
Предположим, что имеются два колебания одинаковой высокой частоты со с различными начальными фазами:
51 = Аг cos (со* + фх);
52 = А2 cos (соt — f фг)»
Разность фаз этих колебаний
ф = фг—фі» ,
Пусть каждое из этих колебаний смешивается с колебаниями гетеродина
Sr = Bcos((ort + фг).
В результате смешения Si и Sr (и фильтрации) получим колебание разностной частоты:
= Ci cos [Ш + (фі—фг)],
а в результате смешения S2 и Sr — колебание разностной частоты
s2 = С2 cos [Qf + (ф2—Фг)]»
Разность фаз двух последних колебаний
(ф2 — фг) — (фі — фг) = ф2 — фі = ф. (1.22)
т. е. разность фаз колебаний разностной частоты равна разности фаз исходных колебаний, или, другими словами, при гетеродинировании фазовые соотношения не изменяются. Этот весьма важный вывод говорит о том, что измерение разности фаз двух колебаний высокой частоты можно, применив гетеродинирование, заменить измерением разности фаз двух низкочастотных колебаний, что выполняется технически проще и точнее. Поэтому гетеродинирование широко используется в современных дальномерных устройствах.