Бурение грунтовых зондов, установка энергетических колодцев

Общие основы измерения расстояний с использованием интерференции волн. Возможность измерения расстояний сле­дует непосредственно из интерференционной формулы (1.93), которую можно записать в виде

Ipe3 = I1 + h + 2VTJl-ycos-j-(ck-d1), (1.95)

где dz — d = b — разность хода интерферирующих волн. Фор­мула (1.95) связывает наблюдаемую интенсивность с разно­стью хода интерферирующих волн.

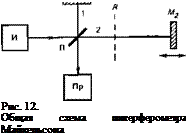
Один из вариантов заключается в создании такой интерфе­ренционной схемы, в которой двойное измеряемое расстояние является разностью хода интерферирующих волн. С принципи­альной точки зрения такая схема вполне соответствует общей схеме рис. 3, реализованной для несущей частоты, и может ис­пользоваться как в оптическом диапазоне, так и в радиодиапа­зоне СВЧ. С технической точки зрения эта схема выполняется в виде той или иной модификации интерферометра Майкель — сона. Не касаясь здесь технических деталей, напомним его^ об­щую принципиальную схему в классическом варианте (рис. 12). Излучение от источника И разделяется полупрозрачной плас­тинкой П на два пучка / и 2. Пучок 1 — опорный, пучок 2 — дистанционный. Опорный пучок отражается зеркалом Мх й про­ходит через пластинку П, а дистанционный отражается зерка­лом ЛІ2 и затем отражается пластинкой П, совмещаясь с опор­ным пучком. При совмещении пучков образуется интерферен­ционная картина, регистрируемая приемником Пр.

Зеркало Mi неподвижно, а зеркало Мг можно перемещать вдоль оси пучка. В частности, если его совместить с плоско­стью R, отстоящей от пластинки П на то же расстояние, что и неподвижное зеркало Mi, то разность хода интерферирующих пучков будет равна нулю. При удалении зеркала Мг от поло­жения R возникает ненулевая разность хода б, равная 2RM2. Таким образом, положение плоскости R задает начало измеряе­мой дистанции D = RM2. Плоскость R называется референтной.

Разность хода можно выразить в длинах волн излучения:

8 — Хр,

где р — некоторое число и соответственно

D = JrP — 0-96)

Число р называется поряд­ком интерференции и выражает собой количество укладываю­щихся на расстоянии D полу­волн. Это число в общем слу­чае — смешанное, т. е.

p = N + AN, (1.97)

где N— целое число; AN — дробь, меньшая единицы, и, сле­довательно,

D = — y(N + AN). (1.98)

Таким образом, если К — длина волны в воздухе — известна, то задача измерения расстояния сводится к определению по­рядка интерференции. Это и осуществляется при помощи интер­ферометра Майкельсона.

Интерферометр в принципе может быть как оптическим, так и радиоинтерферометром. Для достижения максимальной точ­ности измерений в геодезии используется интерферометрия оп­тического диапазона.

В оптическом диапазоне измерения, реализующие формулу

(1.98) , т. е. случай, когда расстояние выражается в длинах волн света, получили название абсолютных интерференционных измерений. При этом для геодезических целей часто доста­точно определить порядок интерференции с точностью до це­лого числа N.

Поскольку длина волны света мала, число N может быть очень велико. Например, на расстоянии всего 1 м оно более 106.

В лазерной интерферометрии, число N определяется мето­дом счета интерференционных полос, представляющим собой реализацию упоминавшегося в § 4 (стр. 40) способа непо­средственного счета N при изменении расстояния. Если рас­стояние D непрерывно изменять, то будет изменяться разность хода интерферирующих волн и в соответствии с формулой (1.95) будет наблюдаться периодическое изменение интенсив­ности света в любой фиксированной точке поля интерферен­ции. При изменении разности хода на X, т. е. при изменении D на К/2, совершается один полный цикл изменения интенсив­ности, что соответствует изменению N на единицу в формуле

(1.98) . Таким образом, для определения величины N необхо­димо «прокатать» удаленный отражатель вдоль всей измеряе­мой дистанции и просчитать число полных циклов изменения интенсивности, т. е. число максимумов или минимумов света.

Таким методом в принципе можно измерять расстояние в пределах длины когерентности лазерного света в атмосфере (несколько сот метров). Однако необходимость перемещения отражателя вдоль трассы требует сооружения точных на­правляющих на местности, что технически сложно и дорого.

Поэтому лазерные интерферометры, за исключением специаль­ных случаев (прецизионные работы в закрытых помещениях), используются для измерения небольших перемещений, а также в режиме стационарного прецизионного слежения, когда инте­ресуются не самим расстоянием, а его изменением во времени. В последнем случае число N не определяется, а непрерывно из­меряется его приращение.

Совершенно другой тип интерференционных линейных из­мерений в оптическом диапазоне представляют собой так на­зываемые относительные интерференционные измерения. При таких измерениях интерференция используется для последова­тельного умножения небольшой, но точно известной (измерен­ной абсолютным методом) длины (эталона) в целое число раз. Относительный интерференционный метод — это не метод из­мерения произвольного расстояния, а, по существу, оптический метод точного построения, откладывания на местности отрезка с длиной, кратной заданной длине эталона. После того как та­кой отрезок точно зафиксирован, он, в свою очередь,, может служить эталоном, который умножается в целое число раз, и т. д. Такой способ дает возможность, например, создавать вы­сокоточные базисы.

Относительные измерения основаны на создании такой — ин­терференционной схемы, в которой возможно точное уравнива­ние оптических путей дистанционного и опорного пучков. При этом дистанционный пучок проходит расстояние 2D, а опорный m раз проходит эталон длиной d, после чего они соединяются и могут интерферировать.

Интерференция будет наблюдаться в том случае, если оп­тические пути уравнены с точностью до длины когерентности источника излучения. Поэтому, чтобы добиться как можно бо­лее точного уравнивания оптических путей, необходимо взять максимально некогерентный источник света. Таким источником является источник белого света, у которого длина когерентно­сти не превышает 2—3 мкм. Таким образом, появление интер­ференционной картины в белом свете служит весьма чувстви­тельным индикатором момента равенства оптических путей света на дистанции и в опорном пучке, позволяя «подогнать» расстояние D под кратное эталону значение с микронной точ­ностью. Необходимость некогерентного источника является спе­цифической особенностью относительного метода, называемого также методом оптического умножения расстояний.

Конкретная схема реализации относительных интерферен­ционных измерений представляет собой ту или иную модифи­кацию интерферометра Вяйсяля (см. § 17).

Интерференционными методами можно измерить не только расстояние, но и разность двух расстояний — d2 и d в формуле (1.93). Это широко используется при интерференции радио­волн и лежит в основе работы фазовых гиперболических си­стем радионавигации (см. § 21). Если источники когерентных

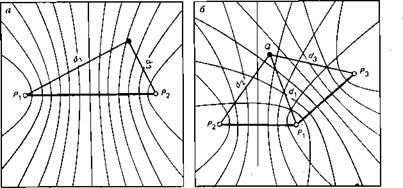
Рис. 13. . Образование гиперболической сетки интерференционных полос, используемой в радионавигационных и радиогеодезических системах

интерферирующих волн находятся в точках Р и Р2 (рис. 13,а), то при сферических волнах интерференционное поле представ­ляет собой систему интерференционных полос в виде гипербол с фокусами в Pi и Р2. Действительно, интерференционные по­лосы— это линии постоянной интенсивности, а из формулу (1.93) ясно, что интенсивность постоянна, если d2—d = const. Но это есть условие, определяющее гиперболы — геометриче­ские места точек постоянной разности расстояний. Если взять три когерентных источника (рис. 13, б), то можно получить две системы пересекающихся гипербол, и местоположение лю­бой точки Q в районе перекрытия определится двумя гипербо­лическими координатами — разностями расстояний (d2—d) и

(d3—d), определяемыми по измерениям разностей фаз 2я х

. Л

x(d2—dx) и —-—(d3—dx) в точке Q.

Л ‘ _

Обобщение понятия когерентности. Нестационарная интер­ференция. В соответствии с классической теорией когерентно­сти это понятие применимо только к колебаниям или волнам с одинаковой частотой (точнее, имея в виду реальные волны, с одинаковой средней частотой). В радиотехнике, однако, ко­герентными называют также колебания различных частот в том случае, если эти частоты не независимы, а связаны оп­ределенным образом (синхронизированы), так что изменение частоты одного колебания влечет за собой изменение частоты другого и отношение частот остается неизменным. Это имеет место, в частности, в когерентных радиогеодезических систе­мах, где когерентность двух (или более) передатчиков обеспе­чивается умножением частоты одного из них.

Особый интерес представляет случай, когда частоты обоих колебаний близки, т. е. случай биений. Биения — это периоди-

ческое изменение амплитуды суммарного колебания, обуслов­ленное интерференцией разночастотных колебаний. В отличие от интерференции колебаний одной и той же частоты, дающей неподвижную, т. е. стационарную, интерференционную картину, при интерференции колебаний с различающимися частотами интенсивность в любой фиксированной точке поля интерферен­ции периодически меняется во времени с частотой биений, рав­ной разности частот складываемых колебаний. Это равносильно движению интерференционных полос через фиксированную точку, т. е. возникает бегущая интерференционная картина. В этом случае наблюдается, как говорят, нестационарная ин­терференция. Причиной нестационарности, как легко понять, является то обстоятельство, что разность фаз двух разноча­стотных колебаний не постоянна, а меняется во времени по линейному закону. . .

Нестационарная интерференция может наблюдаться как для радиоволн, так и для световых волн, получаемых от ла­зера с использованием небольшого сдвига частоты излучения при помощи различных технических устройств. Так как гене­раторы радиоволн и лазеры являются высококогерентными ис­точниками, для них удается наблюдать почти стационарную интерференцию даже от двух независимых однотипных источ­ников, хотя в случае лазеров это требует очень жесткой стаби­лизации оптических частот.

Таким образом, оставаясь в рамках представления о коге­рентности как о способности к интерференции, мы можем рас­ширить понятие когерентности, включив в класс интерференци­онных явлений случай нестационарной интерференции. Другими словами, понятие когерентности не предполагает обязательной неподвижности интерференционной картины; оно связывается лишь с временем наблюдения (усреднения) Т, т. е. с времен­ной разрешающей способностью регистрирующего прибора: колебания когерентны, если приемник сможет зарегистриро­вать интерференционную картину, а это произойдет тогда, когда разность фаз не меняется существенным образом за время Т. Вся система полос перемещается в темпе изменения разности фаз, и чем он быстрее, тем менее инерционный при­емник требуется для обнаружения интерференции. При разно­частотных колебаниях этот темп задается величиной разност­ной частоты (частоты биений).

Использование нестационарной интерференции для измере­ния расстояний. Нестационарная интерференция имеет прямое отношение к интересующему нас случаю дальномерной интер­ферометрии. Так, именно она имеет место при движении зер­кала в лазерных интерферометрах типа Майкельсона, когда производится счет движущихся полос. Обратимся к рис. 12. Перемещение зеркала М2 создает непрерывное изменение раз­ности хода б и, следовательно, разности фаз интерферирующих волн. Если одну из волн (опорную) описывать в точке интер-

ференции функцией cos (о ty то другая волна будет описываться функцией cos сор —Переменная составляющая резуль­тирующей интенсивности (интерференционный член) пропор­циональна косинусу разности фаз, равной со ^ 6 (іt).

V Л

При равномерном движении зеркала из начального положения R со скоростью. V имеем 6(t)=2Vt, и результирующая интен­сивность

)

Формула (1.99) показывает, что результирующая интенсив­ность изменяется во времени — происходит ее модуляция с кру­говой частотой Q=2nF, где F — 2VIX-, F есть частота, численно выражающая скорость прохождения интерференционных по­лос перед фотоприемником (F полос в секунду).

Таким образом, при интерференции двух волн одной ча­стоты со возникает нестационарная интерференция за счет того, что их разность фаз изменяется во времени при движении зер­кала.

Совершенно адекватным образом этот случай можно ин­терпретировать и по-другому, а именно — как интерференцию двух разночастотных колебаний, так как при отражении от движущегося зеркала происходит сдвиг частоты вследствие эффекта Доплера. На приемнике встречаются две волны с раз­личающимися частотами со и ©’, и возникают биения с раз­ностной частотой, т. е. та же модуляция интенсивности с ча­стотой биений, приводящая к движению интерференционных полос. Частота биений определяется формулой для доплеров­ского сдвига частоты:

| со — а’ | = (о —= 2 nF — Q, (1.100)

t) п

т. е. результат совершенно аналогичен полученному выше.

Интерференционное явление биений может быть также по­ложено в основу метода измерения расстояний, в котором осу­ществляются фазовые измерения на частоте биений. При этом режим биений достигается не движением отражателя, а ис­пользованием при неподвижном отражателе двухчастотного источника излучения. Предположим, что мы располагаем та­ким источником, генерирующим две волны с немного отличаю­щимися круговыми частотами кц и 02 и начальными фазами Фі и ф2- Результирующая интенсивность волнового поля такого источника определяется интерференцией этих двух волн и в об­щем случае будет описываться выражением

где г|)(0 — разность фаз волн:

Ф (0 = (ші/+ фі)— (©а^ + фе) = ^ + (фі— фг). (1.102)

Результирующая интенсивность модулирована с частотой биений Q = ©i—©2. Если такое излучение разделить на два пучка и направить один из них на дистанцию, а другой —по опорному каналу, то интенсивность в пучке, прошедшем ди­станцию 2D, будет (потерями при распространении здесь пре­небрегаем):

I диет = ^1"Ь^2’Ь2 ~f III2 • У COS —————- — j — f — (фі — Фг)^ >

(1.103)

а интенсивность в пучке, прошедшем опорный тракт длиной 2d,—

Лшорн = Л + ^а + 2 ^——— ^v~) ”^"^1—’

(1.104)

Принимая дистанционный и опорный пучки на раздельные приемники, можно при помощи фильтров на частоту Q выде­лить только переменные составляющие (последние члены вы­ражений (1.103) и (1.104). Включив между приемниками фазо­метр, можно измерить разность фаз этих составляющих. Она будет

Т“=И’—

_[а(<—^)-НФі-ч4)] =а vd-J) , (1105)

откуда

D = ^-+d,

2Q

или, полагая Q = 2nF — 2п -2—,

А

Таким образом, в этом методе информация о расстоянии переносится на частоту биений, которая гораздо ниже опти­ческих частот ©і и ©2 и лежит в радиодиапазоне. Другими сло­вами, измерения разности фаз световых волн заменяются из­мерениями разности фаз двух сигналов на радиочастоте, что осуществляется проще и надежнее хорошо разработанными радиотехническими методами. Однако при этом теряется «ин­терференционная» точность измерения расстояния, присущая
оптической интерферометрии (т. е. точность порядка длины волны света), так как масштабной длиной волны, через кото­рую выражается расстояние, является уже не длина волны света, а длина волны биений Л, связанная с длинами интерфе­рирующих волн A, i и %2 соотношением

Л = ^— «-Д— (Я—средняя длина волны света)

(1.107)

и превышающая длины световых волн Яі и Яг на несколько порядков (например, она может составлять сантиметры). Уст­ройство, реализующее данный метод, по сути дела, является фазовым светодальномером, в котором явление нестационар­ной интерференции используется не для измерений, а для со­здания модуляции, позволяющей применить фазовые измере­ния на радиочастотах, т. е. фазовый метод. Изложенный прин­цип нашел практическое применение в лазерном дальномере на биениях мод [14, 20].

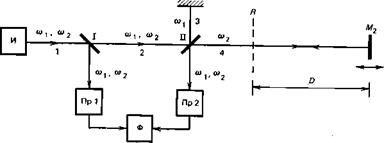
В рассмотренном способе в каждом из пучков интерфери­рующие волны различных частот проходят один и тот же путь (дистанцию или опорный канал). Если же волны различных частот от двухчастотного источника заставить интерферировать после прохождения ими различных расстояний, т. е. напра­вить излучение, например, с частотой ©і в опорный канал, а с частотой ©г —на дистанцию, то оказывается, что можно сохранить интерференционную точность измерений, выполняя фазовые измерения на частоте биений, т. е. построить гетеро­динный интерферометр. Принцип построения такой схемы по­казан на рис. 14. Двухчастотное излучение от источника И раз­деляется светоделителем I на два пучка 1 и 2 обычным обра­зом. Пучок 1 поступает на опорный приемник Пр I, а пучок 2 попадает на второй светоделитель II, разделяющий его на два пучка 3 и 4 так, что к неподвижному зеркалу М направляется излучение с частотой ©ь а к подвижному зеркалу М2 — излу­чение с частотой ©г (техническое осуществление такого деления сейчас нас не будет интересовать). Тогда на приемнике Пр 1 происходит нестационарная интерференция волн с частотами ©1 И ©2, прошедших один и тот же путь I от источника до при­емника, а на приемнике Пр 2 — нестационарная интерферен­ция волн ©і и ©2, прошедших различные пути, отличающиеся на 2Z>. Фазы волн, интерферирующих на приемнике Пр 1, можно записать в виде

(1.108)

(1.109)

Рис. 14. Общая схема гетеродинного интерферометра

Переменная составляющая интенсивности будет пропорцио­нальна величине cos (q>Lt—фе>,) и, следовательно, создаст на вы­ходе приемника сигнал разностной частоты Q с фазой.

ф1 = ф©!—ф©а = Ш—©і ——Ь ©2 ——Ь (фі—фг)* (1.110)

Фазы, же волн, интерферирующих на приемнике Пр 2, можно представить в виде

= (Ull)

ф", = <йа(*— М + 2Р ) + Ф* (1.112)

где 2d означает путь от источника до приемника Пр 2 через неподвижное зеркало М. Переменная составляющая интенсив­ности на этом приемнике будет пропорциональна cos (ф",—ф") и создаст сигнал частоты й с фазой

+».+<*-*>•

(1.113)

Включив между приемниками Пр 1 и Пр 2 фазометр Ф, можно измерить разность фаз:

М, / I 2d . f 2d + 2D I

+«»(—±———— -)■

(1.114)

Поскольку оптические частоты (Ох и ш2 близки, то, положив ©і«(В2=<»> получим:

Ф = С0 —= -^-2D, (1.116)

V К

откуда

к Ф к / ф11

2~ 2л ~ ~2ІЇ

где % — средняя длина волны света.

Как мы видим, результат измерений, выполняемых на раз­ностной частоте биений Q, дает расстояние, выраженное не через длину волны биений, а через длину волны света, как и в обычном интерферометре. Для определения N обычно произ­водится перемещение подвижного зеркала вдоль всей ди­станции.

Рассмотренная схема положена в основу современных ге­теродинных лазерных интерферометров (интерферометров «второго поколения»), техническое устройство и работа кото­рых рассматриваются в §17.

Комментарии запрещены.