Бурение грунтовых зондов, установка энергетических колодцев

Вследствие неравномерной плотности атмосферы электро­магнитные волны распространяются в ней не по прямой ли­нии, а по некоторой кривой. Это искривление траектории волны называется рефракцией.

Для дальнометрии представляет интерес величина удлине­ния траектории, обусловленного рефракцией. Если это удли­нение обозначить ADr, то геометрическое расстояние

Д = А, зм—ADr. (2.58)

Таким образом, учет влияния рефракции сводится к нахож­дению удлинения ADr. Это удлинение зависит от радиуса кри­визны траектории волны.

Можно показать, что в приближении сферической Земли радиус кривизны траектории с достаточной степенью точности определяется выражением

(2.59)

где а — угол, под которым волна входит в атмосферу (угол падения); п — показатель преломления, который можно поло­жить равным единице.

В частности, для небольших углов наклона трассы к гори­зонту, когда можно положить sina=l, ,

1_____ 10*

/ dn ~ / dN dH J [dH )

Из уравнения (2.60) следует, что радиус кривизны зависит не от показателя преломления, а от его градиента и прибли­женно равен его обратной величине. Задача об определении радиуса кривизны траектории сводится, таким образом, к за­даче об определении градиента показателя (или индекса) пре­ломления воздуха.

Градиент индекса преломления. При рассмотрении моде­лей атмосферы указывалось, что наиболее упрощённой явля­ется линейная модель, в которой градиент индекса преломле­ния постоянен и равен (для радиоволн) —40 N-ед/км. Постоян­ство градиента означает, что радиус кривизны в любой точке траектории одинаков, т. е. траектория представляет собой дугу окружности. Подставив значение dN/dH=—40 А^-ед/км в урав­нение (2.60), найдем численное значение для радиуса этой ок­ружности р= 25 000 км. .

Этот результат относится к радиоволнам. Для света ра­диус будет больше, так как световые волны испытывают в ат­мосфере меньшее преломление, чем радиоволны. Это объяс­няется тем, что частота световых колебаний весьма высока и полярные молекулы воды, присутствующей в атмосфере, не успевают при прохождении световой волны менять ориенти­ровку и внести свой вклад в значение показателя преломления. Для света можно в среднем принять р=50000 км.

При повышенных требованиях к учету рефракции необхо­димо более строго подходить к вопросу об определении ра­диуса кривизны. В этом случае нельзя считать траекторию волны дугой окружности, т. е. принимать условие постоянства градиента индекса преломления на всем пути волны’, не соблю­дающееся в действительности. В реальной атмосфере траекто­рия волны представляет собой сложную пространственную кри­вую, у которой радиус кривизны р меняется от точки к точке. Поэтому необходимо определять средний радиус кривизны:

(2.61)

Здесь возникает задача определения среднеинтегрального

градиента индекса преломления

ренной выше задаче об определении <N>, и для ее решения целесообразно использовать также биэкспоненциальную мо­дель атмосферы, как наиболее точную.

Вычисление поправки ADT. При вычислении удлинения ДDT наиболее просто и удобно получить формулу для ADT, считая, что траектория волны — дуга окружности, а при необходимо­сти учета действительной формы траектории использовать в качестве радиуса этой окружности средний радиус кривизны, определяемый формулой (2.61).

На рис. 19 дуга окружности АВ есть измеренное расстоя-
ниє Дим, хорда АВ — искомое геометри­ческое расстояние Dy AO = OB = p — ра­диус кривизны. Обозначив 0 централь­ный угол, соответствующий дуге £>изм, можно написать

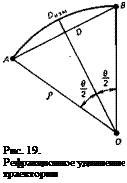^изм = р0» D = 2р sin —.

Разложим sin (0/2) в ряд, воспользо-

х3 ,

вавшись формулой sinх = х—• • • •

Ограничиваясь двумя членами разложе­ния, будем иметь.

£> = рЄ-^-р(^-)8- (2-62)

Отсюда получим

(2.64)

При точных вычислениях, как уже отмечалось, в качестве р следует брать <р>.

Представление о величине поправки ДDr дает табл. 3.

Из табл. 3 видно, что при измерении расстояния примерно 50 км поправка за рефракцию составляет не более 2•10-7 от расстояния. Такая величина при обычных свето — и радиодаль — номерных измерениях может не учитываться (а при необходи­мости может быть учтена по формуле (2.63)). Учет поправки за рефракцию необходим в случае измерения больших (>100 км) расстояний.

Об аномальной рефракции. Все изложенное выше относится к случаю так называемой нормальной рефракции, имеющей

место при обычном, наиболее часто наблюдаемом состоянии атмосферы. Однако конкретные метеоусловия могут сложиться так, что распределение индекса преломления по высоте станет существенно отличаться от обычного. В таких случаях говорят об аномальной рефракции.

Распознать характер рефракции можно, имея эксперимен­тально полученные профили распределения индекса преломле­ния по высоте. Аномальная рефракция не может быть учтена никакой моделью атмосферы, так как она представляет собой случайное, а не закономерное явление. Однако, как правило, аномальная рефракция возникает на ограниченных участках и в ограниченных высотных интервалах, и в целом режим распространения обычно близок к нормальному, за исключе­нием отдельных случаев, встречающихся чаще всего в опреде­ленных климатических зонах (особенно для световых волн).

Комментарии запрещены.