Бурение грунтовых зондов, установка энергетических колодцев

Чтобы вычислить расстояние по уравнению вида (1.32), необходимо определить целое число N и тем самым устранить

зо

неопределенность, неоднозначность этого уравнения. Опреде­ление числа N называется разрешением неоднозначности (или многозначности) и в разных типах фазовых дальномерных устройств проводится различным образом. В свето — и радио­дальномерах в настоящее время используются два основных способа разрешения неоднозначности: способ плавного измене­ния частоты и способ фиксированных частот (применяется также и комбинированный способ). Способ фиксированных час­тот используется и в некоторых типах фазовых радиогеодези­ческих систем. В большинстве фазовых РГС, а также в лазер­ных интерферометрах применяется способ изменения рас­стояния.

Способ плавного изменения частоты. Этот способ, как ясно из названия, используется в дальномерах с переменной часто­той модуляции. Сущность способа состоит в следующем. По­скольку при изменении частоты меняется и разность фаз <р, в диапазоне перестройки можно подобрать ряд частот, при ко­торых <р (а значит, и AN) принимает одинаковые значения при различных N. Эти частоты расположены эквидистантно на час­тотной оси, а их число в диапазоне перестройки зависит от длины измеряемого расстояния. Предположим, что мы выбрали две такие частоты fx и /2; в общем случае их порядковые но­мера на частотной оси отличаются на п. Для двух частот полу­чаем два уравнения:

D =-^-(N1+AN)-, 41	(1.35)
D=-^-(N2+AN).	(1.36)

При измерениях дальномером частоты модуляции Д и /г обычно подбирают так, чтобы <р было равно какой-либо одной из следующих величин: 0, я/2 или я; при этом AN будет соот­ветственно 0, 1/4 или 1/2. Разумеется, в дальномере должен быть соответствующий индикатор, способный фиксировать эти значения. Подобранные указанным образом частоты f и f2 из­меряются каким-либо частотоизмерительным устройством. При перестройке частоты от fx до f2 непосредственным счетом по ин­дикатору определяют величину

П1Л = ^—N* (1.37)

(это соответствует случаю fx<f2; если /,</2, то n2.x=N2— Nx).

Равенства (1.35), (1.36) и (1.37) образуют систему трех уравнений с тремя неизвестными D, Nx и N2, имеющую одно­значное решение.

Приравнивая правые части первых двух уравнений с уче­том третьего уравнения, получим:

N1 + AN = n1.i h ; (1.38)

1.1 “/2

Nt + AN = th* tf • (1.39)

II— /2

В зависимости от того, каким выбрано регистрируемое значе­ние ф, числа Ni+AN и N2 +AN должны быть либо целыми, либо целыми плюс половина, либо целыми плюс одна четверть. Из-за неизбежных ошибок измерений числа, вычисленные по формулам (1.38) и (1.39), могут несколько отличаться от ука­занных значений. Поэтому их надо обязательно округлить до ближайшего нужного значения и только после этого подстав­лять в уравнения (1.35) и (1.36) для вычисления расстояния.

Величина отличия вычисленных чисел N+AN от нужных значений является критерием качества измерений и поэтому строго лимитируется. Чтобы можно было уверенно произвести округление в нужную сторону, отличие должно быть менее 0,5. Практически инструкциями устанавливаются еще более жест­кие допуски.

Неоднозначность разрешается тем уверенней, чем больше разнесены частоты f и /2, т. е. чем больше число hi.2.

Допустим теперь, ЧТО «1.2=1, т. е. фиксируются две ближай­шие друг к другу частоты, при которых наступает одинаковое значение AN (назовем их смежными частотами). Из уравнений (1.35) — (1-37) нетрудно установить, что разность смежных частот 6/ определяется выражением

ч—к — <•«»

т. е. будет тем больше, чем меньше измеряемое расстояние. Очевидно, что существует такое минимальное значение расстоя­ния Dmin, при котором смежные частоты fx и /2 будут разнесены на концы предусмотренного в приборе диапазона изменения ча­стоты так, что следующие частоты, при которых наблюда­лось бы то же значение ф, будут находиться уже за границами частотного диапазона дальномера. Другими словами, во всем частотном диапазоне шириной Д/ будут наблюдаться только две «рабочие» частоты. Чтобы при перестройке частоты моду­ляции в диапазоне изменения частоты Д/ всегда укладывалось бы не менее двух рабочих частот, необходимо выполнение усло­вия

a/<-i-AF. (1.41)

Отсюда получаем минимальное расстояние, которое можно
однозначно измерить дальномером с плавным изменением час­тоты в диапазоне А/:

^mln — vl А/-

В некоторых приборах (например, в советском светодаль­номере СГ-3) для разрешения неоднозначности используется разновидность способа плавного изменения частоты, иногда называемая способом последовательных приближений. Сущ­ность этого варианта заключается в следующем. Из формулы (1.40) следует, 4то

Расстояние, вычисленное по этой формуле, будет тем точнее, чем больше величина 6/ или чем она точнее известна. По­скольку увеличить 6f при заданном расстоянии невозможно, идут по пути ее последовательного уточнения. Расстояние, вы­численное по формуле (1.43) с использованием непосредст­венно измеренного значения 6/ в начале диапазона, является первым приближением. Второе приближение для б/ (а следо­вательно, для D) получают, измеряя разность уже не смежных частот (т. е. первой и второй), а первой и третьей, разделен­ных интервалом 26/, и деля результат на 2. Следующее прибли­жение— измерение частот, разделенных интервалом Щ (пер­вой и четвертой), и деление результата на 3 и т. д. Так про­должается до тех пор, пока очередное приближение длд D будет отличаться от предыдущего не более чем на Я/4, т. е. расстояние становится известным с точностью, необходимой для безошибочного вычисления числа N на любой из рабочих частот в пределах всего диапазона изменения частоты.

При автоматизации этого способа удобно использовать не все приближения, а только кратные 2ft, где k — целое число (т. е. 1, 2, 4, 8-е и т. д.), так как при этом технически упро­щается задача деления частоты.

Способ фиксированных частот. Для однозначного решения уравнения (1.32) при одной фиксированной частоте необхо­димо приближенно знать расстояние D с такой точностью, чтобы при вычислении целого числа N по формуле [следующей из уравнения (1.34)]

ДГ = 2Рприбл _______ ддо

оно было получено верно, т. е. ошибка mN была бы по край­ней мере менее 0,5. Из последнего равенства следует

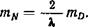(1.44)

Подставив сюда условие mN<0,5, найдем, что £>прибл нужно знать с ошибкой менее Я/4.

Как указывалось в предыдущем разделе, типичные значения масштабных частот лежат в диапазоне 10—500 МГц. При f= 10 МГц А./4 = 7,5 м. Знать с такой точностью достаточно большое расстояние—практически невыполнимое требование даже при наличии крупномасштабных карт. Поэтому дально­меры с одной фиксированной частотой модуляции не могут обеспечить разрешение неоднозначности (за исключением слу­чаев коротких расстояний).

Путь, позволяющий решить задачу, состоит во введении не­скольких фиксированных частот. При т частотах имеем т независимых уравнений:

D =	V 2/1	— (Nx + AN,) — ■	^-(Nl+A N& ‘
D =	V У*	-(Nt + AN2) = —	-^(N2 + AN2y,	(1.45)
D =	V Of	“ (Nm~~ A Wm) —	*m (Nm + ANm),

где все величины AN известны (измерены фазометром), но не­известны все N и D. Решение задачи может быть различным в зависимости от того, как выбраны частоты fu /2,…, /т. Суще­ствуют два основных варианта построения сетки фиксирован­ных частот: 1) метод кратных частот, составляющих ряд

fi>/2> … >/m> и 2) метод комбинационных частот—близких частот, выбранных так, чтобы последовательно уменьшались в целое число раз разности первой и следующих частот; обычно (fl—fm)> (fi—fm-l) >. . .> (fi—/2) . РаССМОТрИМ ПрИН­ципиальное решение задачи для обоих вариантов.

1. Метод кратных частот. Основная идея этого варианта заключается в том, что приближенное значение расстояния, требуемое для определения числа N на каждой частоте, нахо­дится из измерений на следующей более • низкой (меньшей в целое число раз) частоте, для определения N на которой можно знать расстояние более грубо. Для этого каждая более низкая частота должна в то же время быть достаточно высокой для того, чтобы обеспечить получение расстояния с точностью не хуже четверти длины волны предыдущей (более высокой) частоты.

Рассмотрим простой случай двух фиксированных частот. Пусть имеется частота fi и более низкая частота /2, выбранная в соответствии с указанными выше требованиями. Для двух

частот получаем два уравнения:

Предположим, что расстояние заранее известно с точностью не менее W4. Тогда мы можем определить N2 по формуле

N2 = 2РпРибл — Д N2. (1.48)

Округлив полученное таким образом число N2 до ближай­шего целого и подставив его в уравнение (1.47), мы найдем расстояние, определенное на частоте f2. Это расстояние будет представлять собой второе приближение £>’прибл по сравнению с заранее известным значением £>прибл и будет являться тем приближенным значением, которое необходимо для определе­ния N на первой частоте. По этому значению расстояния на­ходим

Ni= 2рпрнбл _AN^ (1.49)

т

округляем его до целого числа и, подставляя в уравнение (1.46), получаем точное значение расстояния D.

Практически можно исключить промежуточную операцию вычисления Я’прибл. Действительно, приравняв правые части уравнений (1.46) и (1.47), получим:

N!=-^~ (N2 + Д#2)—ANlt (1.50)

Ai

и поэтому можно, найдя из выражения (1.48) N2 и округлив его до целого, подставить его в формулу (1.50) и сразу полу­чить верное значение числа N і без промежуточного вычисления

О прибл*

Отношение величин (целое число) ‘

показывающее, во сколько раз грубее можно предварительно знать расстояние при двух частотах, чем при одной частоте, называется коэффициентом неоднозначности. Чем ниже вторая частота, тем больше этот коэффициент. Однако его увеличение лимитируется тем, что при слишком низкой частоте может быть не обеспечена необходимая точность получения /)’Прибл (не гру­бее Ач/4). Следовательно, вторая частота может быть умень­шена по сравнению с первой только до определенного предела.

35

Если при этом требуемая точность предварительного знания ^прибл еще неприемлемо высока, то вводят третью частоту, четвертую и т. д.

Рассмотренный вариант разрешения неоднозначности прост и удобен для автоматизации. Достаточно иметь только один стабилизированный генератор на наиболее высокую частоту fи а остальные частоты можно получить делением частоты ft-

Таким образом, в этом варианте точное значение расстояния получают только на основной (самой высокой) частоте, а остальные частоты используются лишь для расширения диа­пазона однозначно измеряемого расстояния.

2. Метод комбинационных (близких) частот. В этом слу­чае также имеется набор частот fi>f2> •••>fm, но все они од­ного порядка величины, а необходимые ступени уменьшения частот создаются последовательностью —fm)>(f і —

— /m-і) > . •. > (/і — h)- При этом используется то обстоятель­ство, что разность результатов измерений на двух частотах эквивалентна результату измерения на разностной частоте.

Поясним сущность этого варианта также на примере двух частот. Предположим, что имеются две частоты f и /2 одного порядка величины, но при этом f2 несколько ниже, чем fi, так что разность (h—/2) существенно меньше fi. Запишем два

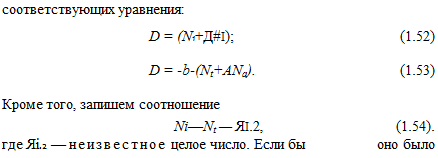известно, то система уравнений (1.52) — (1.54) решалась бы однозначно. Для нахождения П1.2, как будет показано ниже, необходимо опять-таки предварительно знать расстояние Яприбл, но уже с точностью не до Х/4, а с такой, чтобы полу­чить верное значение целого числа пі.2) намного меньшего, чем Ni и N2.

Приравняв правые части (1.52) и (1.53) с учетом (1.54), определив из полученного равенства N і и подставив его в (1.52), получим уравнение

D = (п1Л+ANt—bNa), . (1.55)

2 .

1 __ _______ Ц

~ и-ь

есть длина волны разностной частоты.

Из уравнения (1.55) можно найти /її.2, если заранее изве­стно расстояние D. Определим, с какой точностью требуется его знать. Из (1.55) для ошибок получим

tn2D= -^р-(‘Лпі.2 + mlNl + mN^. (1.57)

Предположим, ЧТО величины Ani и AN2 измеряются безо­шибочно, т. е. mANl = т&ц2=0. Тогда, считая m„I 2<0,5, найдем:

<-т— С-б*)

Коэффициентом неоднозначности в этом случае является величина

/Сі. г=-^- = —(1.59) Лі /і — h

Поэтому условие (1.58) можно записать в виде

<к-Ь~, (1.60)

откуда наглядно видно, что чем больше К, тем грубее можно

знать £>Прибл и тем больше диапазон однозначно измеряемых расстояний.

Однако увеличение коэффициента неоднозначности влечет за собой, как нетрудно установить из формулы (1.57), повы­шение требований к точности измерения разности фаз на обеих частотах (а также к точности самих частот). Поэтому увели­чивать коэффициент неоднозначности можно лишь до тех пор, пока требуемая точность измерения разности фаз не будет пре­вышать возможностей фазоизмерительного устройства дально­мера. Если при этом еще не достигается желаемый диапазон разрешения неоднозначности (т. е. требуемая точность пред­варительного знания Яприбл еще неприемлемо высока), то при­ходится вводить третью частоту, четвертую и т. д. При этом каждая следующая частота должна располагаться все ближе к первой частоте, т. е. разности первой и добавляемых частот должны последовательно уменьшаться. Иногда масштабные частоты нумеруются не в порядке их введения для расширения диапазона однозначности, а в порядке уменьшения их числен­ных значений: fi>/2> • • • >fm — При такой нумерации наиболь­ший диапазон однозначно измеряемого расстояния опреде­ляется разностью первой и второй частот и составляет Ягг/2.

При увеличении числа частот требования к точности изме­рения AN соответственно снижаются. Обычно в дальномерах бывает от двух до пяти масштабных частот. Коэффициенты неоднозначности для различных ступеней могут быть одинако­

выми или различными; обычно они лежат в пределах от 10 до 100. При заданной первой частоте выбор этих коэффициентов определяет конкретную сетку масштабных частот.

При наличии нескольких частот разрешение неоднозначно­сти и определение точного значения расстояния сводится к следующему: решая систему уравнений (1.52) — (1.54) при условии, что /)=£)пРибл, находят Пу2, «|.3, …, затем Nu N2,… и, наконец, точное расстояние D на всех частотах. При этом все величины п и N, получаемые из вычислений, округляют до целого числа и только после этого используют для дальнейших вычислений.

Частным случаем рассмотренного способа фиксированных частот в обоих вариантах (кратные или близкие частоты) яв­ляется так называемый поразрядный способ, наиболее часто используемый в современных дальномерах. Он основан на том, что коэффициенты неоднозначности по всем ступеням одинаковы и равны 10. При таком условии сетка частот целиком опреде­ляется первой частотой. Ее можно выбрать так, что обработка измерений сведется просто к определению десятичных разрядов в значении расстояния без вычисления чисел п и N. При этом самый точный разряд и его доли определяются на первой, са­мой. высокой частоте.

Поясним это для метода близких частот в наиболее общем случае — на примере дальномера с пятью фиксированными час­тотами, пронумерованными в порядке их уменьшения. Для пяти частот при /(=10 можно записать следующие уравнения:

— _ 20„рибл А АГ.

«1.2—— :———- д1»1.2»

*1.2

«1.3 =Ю («1.2 — Ь ANі.*)—AN!.3;

«і* =10 («і. з+ANі. з)—AN1-4;

«і. б =Ю («1.4 + AN1-4)—ANі. ь;

Ni = 10(«i.6+А#і. б)—ANu

D = -^-(N 1 + ДЛМ,

где для краткости обозначено ANu=ANi — AN і (t=2, 3, 4, 5).

Подставляя в последнее из уравнений (1.61) значение N{ из предпоследнего уравнения, затем в полученное равенство значение «1.5 и т. д., получаем новую систему уравнений:

D= -^-(N+ANt);

D=l0^-(«i.6+AA(1.6);

£> = 10*-^(п1.з + ДЛГ1.з); D=104-b-(%2 + AlV1.2).

Если теперь мы выберем такую частоту /]( чтобы Яі/2= 10 м, то уравнения (1.62) примут вид

D=u-Ni + Юм • ANj Z)= Юм «х. ь + Юм-ДЛ^ьз; D = 10м * ^1-4 М — Юм * ДЛ^і.4; D = 10І • П].з + ЮІ • Д#і.8; D — 10м ■ %.j — Ь Юм ■ Д^1.2-

Так как величины ДЛ^ и ANи меньше единицы, это озна* чает, что первые цифры в численных значениях вторых слагае­мых уравнений (1.63) показывают: в первом уравнении — метры, во втором — десятки -метров, в третьем — тысячи мет­ров и т. д. Поэтому если в каждой из разностей ДIV,,- брать только первую цифру после запятой (отделяющей нуль целых), которую обозначим оц, а величину AN і взять со всеми циф­рами после запятой, и, кроме того, приближенное расстояние выразить ЧИСЛОМ целых сотен ТЫСЯЧ метров Оо = £)прибл/10м, то измеряемое расстояние будет представлено в виде

D = 106а0+ 10^‘Оі. їЮ8,Ді. з-J — 10!,fli4-f ДЛ^, (1.64)

т. е. может быть сразу записано числом с разрядами

Яо О1.2 ^1.3 Яц fli.5 , ANu (1.65)

где AN і — единицы метров и их доли; ai.5 — десятки метров И т. д.

При количестве частот, меньшем пяти, сокращается число разрядов, определяемых из измерений, и требования к точно­сти /)Прибл соответственно увеличиваются.

Необходимость знания приближенного расстояния — ограни­чение, присущее дальномеру с фиксированными частотами, но зато для такого дальномера не существует предельного мини­мального расстояния, как для дальномера с плавным измене­нием частоты.

Комбинированный способ. Этот способ, применяемый в не­которых светодальномерах (например, в дальномере Дистомат DI 10), сочетает в себе черты способов плавных и фиксирован­ных частот. Частота плавно изменяется между двумя крайними фиксированными значениями /і и f2, точно известными. Для этого в дальномере имеются два кварцевых генератора на час­тоты /і и f2 и генератор переменной или качающейся частоты (свип-генератор). Таким образом, в этом случае используют уравнения (1.46), (1.47) и уравнение «i.2=^V, — N2, в котором число «і.2 известно, так как оно может быть просчитано при изменении частоты. Следовательно, система уравнений имеет однозначное решение.

Способ изменения расстояния, используемый во многих фа­зовых РГС и в лазерных интерферометрах, основан на непо­средственном счете фазовых циклов при изменении расстояния. При этом число N равно числу полных фазовых циклов. Важно

отметить, что в этом случае формулой вида D = (N + AN]

Комментарии запрещены.