Бурение грунтовых зондов, установка энергетических колодцев

Действие шарошечного долота заключается в том, что при вращении его корпуса шарошки катятся по забою и располо­женные на них зубцы наносят удары по поверхности породы. Таким образом, мы имеем дело с множеством отдельных ак­тов разрушения, взаимно влияющих друг на друга. В один и тот же момент времени происходит разрушение породы в не­скольких участках, расположенных на линиях контакта шарошч ки с забоем. Что касается последовательно происходящих явлений, то в зависимости от конкретной конструкции долота возможны различные варианты взаимного расположения лунок. Картина взаимодействия осложняется еще и тем, что каждое отдельное внедрение зубца протекает не свободно, а зависит от соприкосновения с породой других зубцов, вследствие чего, нагрузки перераспределяются. Не следует забывать, что поло­жение корпуса долота не зафиксировано вдоль продольной оси и характер внедрения зубцов отнюдь не определяется исклю­чительно законом вращения шарошек.

Выше было показано, что целью расчета кинематики дви­жения долота должно быть определение величины максималь­ного углубления зубцов шарошек zmax в породу при установив­шемся режиме работы всего бурового агрегата. Составить урав­нение движения долота на забое, учитывая абсолютно все детали его конструкции и все подробности характера его взаимодействия с забоем, очевидно, не представляется возмож­ным. К тому же в этом нет никакой необходимости, так как излишняя детализация помешала бы выявить общие законо­мерности и чрезвычайно запутала бы исследуемые явления. Поэтому, естественно, пришлось прибегнуть к определенной схе­матизации. Можно представить — себе несколько различных кинематических схем, моделирующих работу реального долота ка забое скважины. В зависимости от конкретной поставлен­ной задачи, от того, является ли она исследовательской или расчетной, от аспекта ее постановки могут потребоваться ва­рианты моделирования различной сложности. Ниже приведены некоторые возможные расчетные схемы кинематики шарошеч­ного долота, располагаемые в порядке возрастания их слож­ности, и подробности моделирования реального процесса.

Вначале рассмотрим случай, когда долото моделируется одной цилиндрической одновенцовой шарошкой, т. е. зубчатым катком. При этом имеется в виду, что длина зубцов, разме­щенных на этой шарошке, и ширина площадки их притупления таковы, что они соответствуют средней длине и средней ширине площадки притупления зубцов всех венцов трех шарошек до­лота, одновременно находящихся в контакте с забоем. Таким образом, осевая нагрузка на долото, распределяемая между группой контактирующих в каждый момент зубцов реального долота, в данной схеме прикладывается к единственному моде­лирующему зубцу. При этом будем считать, что этот зубеи принадлежит венцу, разбуривающему кольцевой участок за­боя, расположенный симметрично между центром и перифе­рией скважины. Если из середины этого кольцевого участка восстановить перпендикуляр до пересечения с реальной осью шарошки, то длина этого перпендикуляра может быть принята за радиус эквивалентного цилиндрического зубчатого катка. Это ясно из того, что точки на оси шарошки имеют скорости относительного движения, равные нулю, и, следовательно, ско­рость их переносного движения при вращении долота является их абсолютной скоростью. Таким образом, мы заменяем долото цилиндрическим катком, центр которого движется с постоянной горизонтальной скоростью w. Величина w определяется как окружная скорость долота на среднем радиусе и зависит толь­ко от скорости вращения долота п.

Для расчета количества зубцов, размещенных на модели-, рующем зубчатом катке, практически поступают следующим образом. Составляют таблицу, в которой в каждую строку по­мещается количество зубцов данной шарошки, относящихся условно к одной образующей, и фиксируются размеры этих зубцов. Таким образом, каждой образующей можно сопоста-‘ вить один эквивалентный зубец. Затем определяют средние характеристики этого зубца по каждой шарошке и количестве таких зубцов по всей окружности. В заключение остается вы­числить среднюю ширину площадки притупления для зубцов трех шарошек и среднее их количество по окружности, а также суммарную длину зубцов, моделирующих работу всех трех шарошек одновременно. Для штыревых долот можно поступать аналогично, осредняя радиусы скругления вершин штырей. Нетрудно понять, что в результате такой замены шаг зубцов модельного зубчатого цилиндрического катка будет меньше, чем шаг любого венца действительной шарошки, как и должно быть в действительности с учетом возможного перехода кон­такта с одного венца на другой.

Итак, выше дано описание простой модельной схемы буро­вого долота, в которой известны все параметры — конструктив­ные и кинематические, характеризующие зубчатый, цилиндри­ческий, поступательно движущийся каток. Известны количество и размеры его зубцов, горизонтальная проекция скорости и ра­диус катка.

Описанная модель кинематически на первый взгляд мало похожа на натурное долото, но тем не хменее она сохраняет специфику вертикальных перехмещений корпуса и их связь с глубиной внедрения зубцов в породу. Такая модель пригодна для решения некоторых специальных задач, не рассчитанных на количественное определение показателей процесса бурения, но позволяющих сделать оценки влияния различных конструк­тивных особенностей бурильной колонны и входящих в нее эле­ментов на процесс разрушения забоя. Она также позволяет ■сделать приближенные оценки влияния некоторых конструк­тивных параметров долота, таких, как шаг и количество зуб­цов, и параметров режима бурения на величину углубления зубцов в породу.

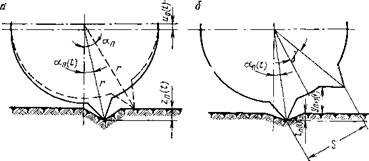
Рис. 4. Схема к расчету: а — глубины внедрения зубца; б — расстояния очередного зубца от поверх­ности забоя

Схема, описанная выше, представлена графически на рис. 4, а. Из схемы ясно, что изхменения интересующей нас вели­чины zn(t) связаны с поворотом шарошки и продольным пере­мещением центра зубчатого катка соотношением

(t) = г [cos ап (t) — cos ап] — [и0 (t) — и0п], (2.1)

где zn — текущее углубление я-го зубца в породу; г — радиус цилиндрического катка; ап — текущий угол хмежду радиусом вершины зубца и вертикальной осью; ап — угол между ради­усом вершины я-го зубца и вертикальной осью в момент сопри­косновения (я—1)-го зубца с поверхностью породы; щ — теку­щее вертикальное перехмещение центра катка относительно

выбранного начала координат; и0п — вертикальное перемеще­ние центра катка в момент соприкосновения с породой п-го зубца.

Текущее значение угла an(t) определяем из следующего — соотношения:

(2.2>

r sin ап — г sin ал (/) == wt,

где w — горизонтальная скорость центра зубчатого катка. Отсюда

w — 2nnR,

Очевидно, что

(2.3>

где R— средний радиус моделируемого долота, соответствую­щий рассматриваемому венцу; п — число оборотов в минуту моделируемого долота.

Скорость w может изменяться во времени при наличии кру­тильных колебаний нижнего сечения колонны труб или любых: устройств, к которым прикреплено долото.

Если зададимся постоянным числом оборотов долота, то его* действительная угловая скорость будет складываться из по­стоянной скорости вращения и дополнительной угловой ско­рости, которая определяется наличием крутильных колебаний: колонны бурильных труб, вызываемых изменениями крутящего момента при работе долота,

(2.4)

где 0 — угол поворота нижнего сечения колонны труб относи­

тельно его центра; со= —угловая скорость вращения до-

30

лота.

(2.5>

Поэтому в общем виде следует считать, что w = w(t). В этом случае формула (2.2) примет вид

г sin ап — г sin ап (t) == j w (t) dt,

где t — момент вступления в контакт с забоем л-го зубца — катка.

В соответствии с этим

an (t) = arc sin sin an J w (t) dt] . (2.6)

Такая форма определения ап требуется при учете крутиль­ных колебаний долота. Этот вариант будет нами та_кже рас­
смотрен. В большинстве же случаев можно считать, что ш = const.

При подходе к поверхности забоя следующего (л-|-1)-го зубца необходимо контролировать его расстояние от забоя. Это расстояние yn+i(t) определяется следующим образом (рис. 4, б):

Уп+i (t) = S sin [у + ап (01 — zn (t), (2.7)

гдь S — шаг зубцов катка по хорде; у — половина централь­ного угла между двумя соседними зубцами.

Вступление в контакт с забоем (/г-!-1)-го зубца соответст­вует моменту t, когда yn+i = 0. При этом угол подхода (л-И)-го зубца может быть вычислен по формуле (см. рис. 4, б)

«л+1 = у + arc cos-^ |/ S2 — [zn (t)f. (2.8)

и

Таким образом, мы располагаем всеми нужными соотноше­ниями для расчета положения каждого зубца катка относи­тельно выбранной системы координат в любой момент времени при условии, что будет известна величина Uo(t). Одновременно она определяет текущее положение нижнего конца колонны бурильных труб, к которой присоединено долото. Поэтому ее вычисление связано с решением уравнения колебаний колонны, о котором речь пойдет ниже.

Изложенная схема кинематики шарошечного долота имеет, как уже указывалось, вполне определенную ограниченную об­ласть применения. Рассмотрим теперь некоторые другие вари­анты кинематических схем, более точно моделирующих конст­рукцию реального долота.

Пусть модель включает три последовательно расположен­ных цилиндрических катка одинакового радиуса, центры кото­рых расположены на одинаковом расстоянии от поверхности развернутого забоя. В этом случае каждый из трех зубчатых катков моделирует одну из шарошек долота. Отличие этой схе­мы от предыдущей заключается в том, что осреднение количе­ства зубцов и выбор средней длины каждого моделирующего катка производятся независимо для каждой шарошки. В дан­ной расчетной схеме зубчатые катки имеют в принципе разную длину и различное количество зубцов. Они могут иметь также разные контактные площадки на зубцах. Поэтому углубление л-го зубца и другие кинематические характеристики движения вычисляются в каждый момент времени для всех трех катков независимо. Обозначая через пг— 1, 2, 3 номер соответствую­щего катка, можно переписать формулы (2.1), (2.3), (2.7) и (2.8) в следующем виде:

2пт (0 = г [COS апт (t) — cos апт) — [щ (t) — и0пт];

, • ! ■ ~ wt

апт (t) = arc sin f sin anm — j;

(2 9)

Уп+i, m (0 = sm sin [ym + anm (/)] — znm (/); v ‘

-l arc cos -1- — [znm (?m)]2

«

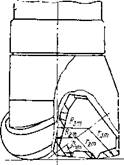
Рис. 5. Схема к моде­лированию шарошеч­ного долота

Дальнейшим приближением модели кинематики долота к действительности является учет конической формы ша­рошек и различие в конструкции от­дельных венцов на них.

Итак, пусть долото состоит из трех конических шарошек, на каждой из которых имеется некоторое количест­во венцов. Каждый венец включает определенное число зубцов и, следо­вательно, имеет различный шаг между ними (рис. 5).

Аналогично предыдущему можно вычислить углубления п-го зубца k-vo венца т-й шарошки, но при этом сле­дует учитывать, что вычисления ведут­ся в плоскости венца и, следовательно, необходимо учесть угол наклона этой плоскости к участку поверхности за­боя, обрабатываемому этим венцом,

*пкт (0 =rkm [cosa„ftm {t)~cos ankm) cosPfem—[u0{t) — u0nkm], (2.10)

где r,.m — радиус k-ro венца m-й шарошки; $кт — угол наклона — оси шарошки к участку поверхности забоя, обрабатываемому данным венцом в вертикальной плоскости, проходящей через ось долота и шарошки.

Соответственно текущий угол поворота зубца в плоскости венца запишем в следующем виде:

= arc sin ^sin ankm (2.Ц)

V r km J

где wkm = 2nnRkm— горизонтальная скорость центра k-го венца m-й шарошки; Rkm— радиус центра венца относительно оси долота.

Расстояние зубца, подходящего к забою, от поверхности бу­дет иметь вид

Уп—,km (f) Wl ® Рбга (0> (2.12)

где yhm— центральный угол вершин двух соседних зубцов k-то венца m-й шарошки; Shm — шаг между этими зубцами по хорде. .

Наконец, величина угла an+i. km(t) в момент вступления его в контакт с забоем

“n+l. Am = У km + аГС COS

Усовершенствованная модель кинематики шарошечного до­лота, списываемая формулами (2.10) — (2.13), позволяет изу­чать зависимость показателей работы долота от конструктив­ных параметров, определяющих его кинематическую схему, и прежде всего от шага зубцов на различных венцах шарошек. Вопрос о выборе шага зубцов является одним из наиболее сложных при конструировании буровых долот. Поэтому целе­сообразно использовать последний вариант кинематического описания долота главным образом для решения конструктор­ских вопросов при проектировании и для решения задачи о вы­боре типа долота, предназначенного для разбуривания опреде­ленного пласта горных пород.

Комментарии запрещены.