Бурение грунтовых зондов, установка энергетических колодцев

Колонна бурильных труб в определенных условиях может оказывать серьезное влияние на процесс разрушения забоя скважины долотом. Трехшарошечное долото является генера­тором механических колебаний. Получая энергию вращения, долото частично преобразует ее в энергию ударов зубцов по забою, а частично в энергию вертикальных перемещений си­стемы. Если бы положение корпуса долота было зафиксировано, то глубина внедрения зубцов определялась бы исключительно геометрией шарошек. В действительности она является алге­браической суммой перемещения зубцов, вызванного вращением шарошки, и перемещения нижнего сечения колонны. Следова­тельно, эффективность процесса бурения во многом зависит от упругих свойств колонны труб и других элементов, входящих в компоновку низа.

Через бурильные трубы проходит целый спектр продольных, крутильных и поперечных колебаний различного происхождения. Существенное влияние на процесс их распространения оказы­вают факторы, влияющие на диссипацию энергии вдоль тракта: свойства материалов колонны и других элементов компоновки, параметры бурового раствора и пр. В случае отражения упругих волн часть энергии возвращается к долоту, изменяя процесс взаимодействия зубцов с породой, а также процесс формиро­вания забоя.

В настоящей главе проводится исследование продольных колебаний колонны бурильных труб. Инструментом исследова­ний является математическая модель процесса бурения, опи­санная выше.

Бурильная колонна в общем случае рассматривается как составной длинный стержень с постоянным сечением на каждом участке. Между участками могут быть вставлены упругие или упруго-вязкие элементы, соответствующие амортизаторам, отра­жателям и подобным устройствам.

Места стыковки этих участков и вставных элементов также могут обладать свойствами отражения и поглощения энергии упругих колебаний.

Долото неподвижно скреплено с колонной, и всякое пере­мещение корпуса долота является одновременно перемещением нижнего сечения колонны.

При расчете колебаний необходимо учитывать сопротивление среды. Для этого в уравнение колебаний (см. главу 2) была

введена постоянная демпфирования и. Наличие в уравнении

, ди и, ди

члена Л — = — — предполагает, что силы трения пропорцио­нальны линейной скорости перемещения сечения колонны, т. е. трение носит вязкий характер. В действительности имеет место одновременно несколько видов трения, однако полный их учет существенно усложнил бы исследования. При чисто вязком трении коэффициент демпфирования р связан с параметрами волнового процесса следующим образом [16]:

2ЕА. а, ,А1

и = In — J-, (4.1)

а2Т а2

где «I, а2 — амплитуды колебаний двух сечений трубы, отделен­ных длиной волны, определяемой периодом колебаний Т.

Амплитуды ах и а2 определяются экспериментально.

Период колебаний зависит от их типа. Долото генерирует высокочастотные продольные колебания, вызываемые прерыви­стым контактом зубцов с породой, а также низкочастотные колебания, причиной возникновения которых, по-видимому, являются неровности (ухабы) забоя.

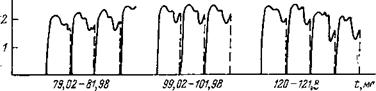
Рассмотрим для начала простейший случай высокочастотных колебаний, отражаемых от сечения колонны, расположенного на расстоянии / от долота. На рис. 37 представлен рассчитанный

2, мм

frrr

19,0- 21,9В

39,02-41,98 59,02-61,98 t, MC

-тек

Рис. 37. Расчетные величины углублений зубцов долота в породу с учетом влияния энергии отраженных волн

по модели процесс развития углуб­ления зубцов в породу. Из рис. 37 видно, что возврат энергии упругих бо ^ j ■■—— волн приводит к увеличению глуби­

£l.

Ш,%

			ЛЕТ
		1 1	У5Т
		1 1 1	|
		1 1	1 1 1

0,0001 0,001 0,01 0,000 0,020

ны внедрения.

цо- ——— —I— X: — Разумеется, это увеличение в

сильной степени зависит от посто — 20 —■——I— 1 ] — янной демпфирования р, определя­

0,1

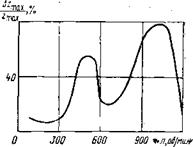
ющей приток энергии отраженной волны. На рис. 38 представлен график изменения относительного углубления зубцов долота в породу Рис. 38. Расчетная зависимость Д Zm„_/Zina_ за счет энергии отра-

относительного приращения ве — шал.^ишл г

личин углублений зубцов доло — женной волны при разных значени — та за счет энергии отраженных ях коэффициента затухания, а сле-

волн от коэффициента затуха — довагельно, и постоянной демпфи-

ния рования. Здесь zmax— возможное

максимальное внедрение зубцов до­лота при отсутствии отраженных волн; Л2тах— приращение уг­лубления за счет энергии отраженных волн.

Как видно из рис. 38, величина коэффициента затухания существенно сказывается, начиная с Х = 0,004, что соответствует коэффициенту затухания для нормальных бурильных труб [16]. Коэффициент затухания для утяжеленных бурильных труб при­близительно равен по тем же данным X = 0,024. Таким образом, величина AzmSiX/zmaiX для утяжеленных бурильных труб в 2 раза меньше, чем для нормальных.

Полученные результаты указывают на практическую воз­можность использования разного рода отражательных систем для повышения эффективности бурения. З’то повышение можег быть весьма значительным в случае, если дополнительный при­ток энергии позволит преодолеть предел прочности породы при некотором недостатке осевой нагрузки. Фазы прямой и отра­женной волн при интерференции, как правило, не совпадают. В результате этого часть возвращенной энергии тратится на сопротивление выходу зубцов из лунки. Этот вредный эффект можно уменьшить, находя нужное соотношение длины отра­жающего участка и скорости вращения долота.

Было исследовано влияние параметров режима бурения на величину углубления зубцов долота при наличии дополнитель­ной энергии отраженных волн.

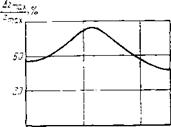
На рис. 39 приведена зависимость изменения относительного углубления зубцов долота в породу от осевой нагрузки на долото. Если нагрузка достаточна или, наоборот, настолько мала, что приток дополнительной энергии все же не позволяет преодолеть предел прочности породы, то выигрыш в величине углубления будет меньше.

Рис. 40. Расчетная зависимость относительного приращения вели­чин углублений зубцов долота за счет энергии отраженных волн or скорости вращения

J-7

Рис. 39. Расчетная зависимость относительного приращения ве­личин углублений зубцов доло­та за счет энергии отраженных волн от осевой нагрузки

zo

На рис. 40 показана зависимость Дгтах/гтах от скорости

врашения дол ста п. Этот график носит явно выраженный резо­нансный характер, т. е, для данной длины отражающего участка существуют свои критические скорости, при которых приток дополнительной энергии к долоту резко возрастает. При изме­нении длины отражающего участка критические скорости ме­няют свое численное значение.

Зная конструктивные параметры долота и длину отражаю­щего участка, можно рассчитать численные значения критиче­ских скоростей, при которых максимальное углубление зубцов долота резко возрастает после возврата отраженных волн.

Для определения влияния материала бурильных труб на характер процесса разрушения расчеты выполняются для со­ставных компоновок, например, утяжеленные бурильные тру­бы — нормальные бурильные трубы; утяжеленные бурильные трубы — легкосплавные бурильные трубы.

Для расчета этих вариантов колонну бурильных труб разде­ляют на два участка, которые описываются волновыми урав­нениями с разными величинами скорости звука а и площади сечения А.

Соединение нормальных бурильных труб с УБТ принимается жестким, следовательно, общее сечение бурильных и утяжелен­ных труб испытывает одинаковые смещения и усилия.

Из этого следует совокупность условий, которые должны быть удовлетворены в месте стыка труб (сечение х=1):

x=h

Х=1х

(4-2)

где и (х, t) —• смещение сечения утяжеленных бурильных труб в момент времени t; й(х, t) — смещение сечения нормальных

u(lx, t) = u(l1, t);

бурильных труб в момент времени t; Е, — модуль упругости УБТ; Е2 — модуль упругости НБТ; Ах— площадь поперечного сечения УБТ; А2 — площадь поперечного сечения НБТ; 1Х — длина УБТ.

При расчете продольных перемещений колонны бурильных труб, состоящей из участков различного сечения, можно вос­пользоваться выведенными ранее (§ 3 главы 2) разностными соотношениями (2.31). Однако на участках стыка труб в общие расчетные формулы должны быть внесены уточнения, учиты­вающие уравнения (4.2).

Действительно, исходя из общих формул (2.31), перемещения последнего сечения нижнего участка колонны и первого сечения второго участка будут равны

— Шип/ ——Ь — . , .

Ми /4-1 — * I 1*^)

1 + ш

= шйй! — й0 7_, +йи + й_1— gt*

=——————— пг^—————- •———— 14л)

Из граничного условия (4.2) следует, что йп. я-i — йо. /+ь и поэтому, приравняв выражения (4.3) и (4.4), получим

‘kMu. Qj— Uo. j—i — f — U-ij — j — M_i/ = ЯДtunj— Un. j—l Un+i. j «n—i./. Учитывая, что йоj = unj и йо. j-i = йп. i-u будем иметь

Uij + W—1/ = Un+i. j — f — Un—.j

или

TOC o "1-5" h z Un+i. i = — «п-1./ + u-ij. (4.5)

Из условия (4.2) также следует, что

j? Л Un+l. j — Unj _ р л “О/ — Н-1/

C-lHl — -=—— — =

Дх Дх

или

= = Е. Л.Дх — , Е. Л.Дх —

И—1/ — «о/ Г — «п+1./ I ~ Uny

Е.2А2 Дх Е2А2 Дх

Подставив значение й-i/ в соотношение (4.5) и решив его относительно йп+. /, получим

Ип+1./ = ия} 4 — (йц — ип-1 ./)• (4.6)

Е. Л.Дх! + —- — £2Л2Дх

Подставляя полученное выражение для un+i. j в формулу

(4.3) , можно рассчитать перемещения йп. j-t-i = «о. /-и в любой момент времени t = At(j+l).

Результаты сравнительных расчетов составной колонны, со­стоящей из УБТ, колонны стальных или легкосплавных труб показали, что среднее значение внедрения зубцов при исполь­зовании легкосплавных труб приблизительно на 10% больше, чем при использовании стальных.

Аналогично проводятся расчеты для произвольной компо­новки из нескольких участков колонны бурильных труб.

Экспериментальными исследованиями установлено, что в ряде случаев наряду с высокочастотными колебаниями, вызы­ваемыми прерывистым контактом зубцов долота с забоем, боль­шое значение могут иметь низкочастотные колебания, возни­кающие, очевидно, вследствие развития на забое так называемых ухабов. Амплитуда этих колебаний обычно больше высоко­частотных.

В связи с этим разработан алгоритм для исследования с помощью математической модели низкочастотных колебаний при перекатывании шарошек по ухабистому забою с частотой

v = л/ 3.

Низкочастотные колебания задаются волнообразной формой забоя

(4.7)

где с — высота точек забоя относительно плоскости, проходя­щей через впадины ухабов; В — амплитуда ухабов: п — число оборотов долота; t-—текущее время.

При расчете углубления каждого очередного зубца его ис­ходное положение контакта с забоем определяется в соответ­ствии с уравнением (4.7). Поэтому долото катится, поднимаясь и опускаясь по ухабам. По этой причине углубления в раз­личных точках забоя могут оказаться неодинаковыми, что приводит к изменению конфигурации самих ухабов. Более того, расчеты показывают, что углубление в отдельных точках может оказаться отрицательным, что соответствует физически нару­шению контакта или отрыву долота от забоя. Таким образом, математическая модель дает возможность оценить эту важную сторону процесса взаимодействия долота с забоем.

Для того, чтобы механизировать процесс расчета последо­вательно изменяющейся конфигурации забоя, можно поступить следующим образом.

Окружность, обрабатываемую данным венцом, разворачи­вают и разбивают на значительное количество мелких интер­валов, на каждом из которых действительная высота забоя первоначально задана в соответствии с уравнением (4.7). При развитии процесса бурения для каждого контакта зубца с по­родой фиксируются его координаты по окружности и высоте. Таким образом, вновь образовавшиеся лунки видоизменяют
конфигурацию забоя в окрестности точки контакта. Постепен­ное слияние лунок (см. главу 1) приводит к изменению перво­начальной формы ухабов и всей конфигурации забоя. Допол­нение к алгоритму расчета углублений заключается в учете и запоминании осевых координат точки, соответствующей контакту данного зубца, и всех точек, определяющих конфигурацию обра­зовавшейся лунки с шагом, соответствующим разбивке забоя на указанные выше участки.

Фактическая высота каждой точки забоя учитывается также при контроле расстояния от забоя очередного зубца. Для этой цели вносятся соответствующие поправки в формулы § 1

главы 2.

Такой подход позволяет, используя математическую модель процесса бурения, проследить за влиянием колебаний колонны на глубину внедрения зубцов и изменение конфигурации забоя по сравнению с принятой исходной формой с тремя симметрич­ными ухабами по забою.

Заметим, что математическая модель позволяет не только задаться волнообразной формой забоя, но и проследить за про­цессом образования ухабов, исходя из первоначальной плоской формы забоя. Для этого также используется метод построения непрерывно изменяющейся поверхности забоя. Таким образом, можно проследить, как через несколько оборотов долота в силу случайного сочетания взаимодействия лунок начинают посте­пенно образовываться и развиваться ухабы.

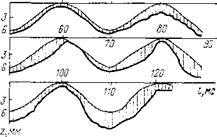
Для записи этого процесса следует использовать ЭВМ высо­кого класса с большим быстродействием, чтобы иметь воз­можность проследить за достаточно длительным процессом формирования и изменения забоя. На рис. 41 представлены конфигурации забоя, рассчитанные для нескольких моментов времени после начала бурения на плоской поверхности.

На основе изложенного выше были проведены расчеты

Е мм ■ Рис. 41. Формирование ухабов на за­бое, рассчитанное на ЭВМ

углублений зубцов долота для разных пород и при различных сочетаниях вы­соты ухабов, осевой нагруз­ки на долото и скорости его вращения. Расчеты подтвер­дили, что в определенных условиях возникают отрывы долота от поверхности за­боя. Это могут быть микро­отрывы, возникающие при движении по склонам уха­бов и не изменяющие об­щей картины взаимодейст­вия долота с забоем, или отрывы, более длительные,

главным образом при на­личии отраженных волн.

Рис. 42. Расчетные величины углуб­лений зубцов долота на ухабистом забсе

Суммарное время отры­ва долота. за оборот в зна­чительной степени зависит от скорости вращения доло­та, осевой нагрузки и высо­ты ухабов. Оно тем меньше, чем ниже число оборотов п, больше осевая нагрузка G и меньше высота ухабов В.

Так, в одном из расчёт­ных вариантов при п =

= 500 об/мин, G = 20 тс и В = 6 мм время отрыва со­ставило 13% от общего времени. При увеличении скорости вращения до п=1000 об/мин оно увеличивалось до 20%. На рис. 42 приведены последовательно изменяющиеся глубины внедрения зубцов на различных участках ухабистого забоя с течением времени. Они существенно различаются на различных участках ухабов. Общий вывод, который позволяют сделать приведенные расчеты, заключается в следующем.

В зависимости от сочетания геометрических параметров ухабов с режимами бурения наибольшая величина углубления зубцов может приходиться на подъем или спуск ухабов, и тогда они начинают перемещаться по забою по ходу или против хода вращения долота. Аналогично наибольшее углубление зуб­цов может приходиться на вершину или впадину ухаба, благо­даря чему высота ухабов возрастает или уменьшается. Этот процесс может оказаться периодическим.

С учетом энергии отраженных волн углубления зубцов мо­гут быть увеличены в значительно большей степени, чем в случае плоского забоя. Таким образом, на эффективность про­цесса разрушения в большей степени влияют низкочастотные колебания колонны, чем высокочастотные.

Метод анализа влияния колебаний на процесс бурения с по­мощью математической модели позволяет оценивать эффек­тивность различных поглощающих и отражающих элементов, входящих в состав колонны бурильных труб. Наличие таких элементов оказывает заметное влияние на максимальное внед­рение зубцов долота в породу, поскольку они эквивалентны амортизирующим и отражающим устройствам. Влияние отра­жающих устройств частично было рассмотрено выше.

В качестве примеров устройств, преобразующих или погло­щающих энергию упругих колебаний, рассмотрим модели пру­жинного и резинового амортизаторов.

При моделировании пружинный амортизатор будем рассмат­ривать как сечение колонны, не имеющее конечной осевой про­
тяженности, но обладающее специфическими упругими свой­ствами. Если это сечение разделяет два участка колонны труб с различными характеристиками, то можно записать

(4.8)

= ш = е2а2 —

дх ’

где k — жесткость пружины; Д/— деформация пружины.

Соотношения (4.8) являются уравнениями равновесия. В то же время они связывают деформации крайних сечений двух участков колонны труб с упругими свойствами пружины.

При расчете колебаний такой компоновки на ЭВМ следует учитывать граничные условия на стыке участков колонны, вы­текающие из (4.8).

При расчете такой компоновки также можно воспользоваться выведенными ранее (§ 3 главы 2) разностными соотношениями (2.31). Проработке подлежат расчетные формулы, определяю­щие перемещения верхнего сечения колонны бурильных труб, находящихся под пружинным амортизатором, и нижнего сечения участка колонны над ним.

(4.9)

Исходя из ранее выведенных общих формул (2.31) расчета продольных перемещений колонны для перемещений верхнего сечения первого участка колонны, будем иметь соотношение

ХД tunj — и

1 л-ш

и соответственно для перемещений нижнего сечения второго участка колонны

-f «1/ — к_, I — gAt2

(4.10)

U0./+I =

лДtuQj Uq j—j | u^j

1 +Ш

Для расчета перемещений по формулам (4.9) и (4.10) сле­дует определить значения перемещений йп+i. j и й-ц на фик­тивных слоях i = n + 1 и г = — 1.

(4.11)

Из граничного условия (4.8) следует, что

+ k (un] — u0J) = 0;

и

(4.12)

Решим первое уравнение (4.11) относительно un+i. j и второе (4.12) относительно u-ij

Подставив значения un+.j и й-ij соответственно в выраже­ния (4.9) и (4.10), получим формулы для расчета перемещений на стыке участков колонны.

Поскольку в эти уравнения входят параметр пружины k, при расчете эффективности бурения появляется возможность варьи­ровать характеристиками пружинного амортизатора.

При моделировании резинового амортизатора будем исходить из предположения, что он представляет собой участок резиновой трубы, вставленный между двумя участками колонны буриль­ных труб.

ф д3и

Учитывая нелинейность резины и наличие поглощения энер­гии в ней, можно записать [25, 26].

2

2лсо dx2dt

где Е3 — модуль упругости резины; ф — коэффициент поглоще­ния энергии в пружине; со — частота импульсов в колонне; Р — коэффициент нелинейности.

3

Это волновое уравнение составлено из предположения, что напряжения и деформации в резине связаны зависимостью

(4.16)

В этом соотношении содержатся нелинейный член и член поглощения в одном из вариантов.

Таким образом, расчет ведется последовательно по участ­кам с использованием уравнений (2.16) и (4.15). Условия стыка участков могут быть записаны следующим образом.

Для нижнего конца резинового амортизатора

(4.17).

= оАа;

и — и.

Для верхнего конца резинового амортизатора

ди

(4.18)

дх

вА3; и — и.

Для расчета продольных перемещений колонны бурильных труб уравнения (2.16) (см. главу 2, § 3) были заменены раз-

постными соотношениями и выведены общие расчетные фор­мулы (2.31).

Для расчета перемещений сечений резинового амортизатора должны быть выведены аналогичные формулы. С этой целью в уравнении (4.5) заменяем производные конечными разностями и получаем соотношение

_|_ £3_i_ ыН-|-/ 2 иЧ ‘

Ах2 At

= Р

(4.19)

Проведя необходимые преобразования и решая полученное

разностное уравнение относительно м,-. дн, получаем формулу для расчета продольных перемещений резинового амортизатора

1 4

Е,

ра‘

2т

Щ—1./ + и 1—1./ /

2я<

ра2Лх2

(4.20)

Соответственно разностными уравнениями заменяются гра­ничные условия (4.17) и (4.18) на стыке резинового амортиза­тора и колонны бурильных труб. Вывод формул расчета про­дольных перемещений на стыке колонны бурильных труб и резинового амортизатора аналогичен приведенному выше вы­воду формул для расчета перемещений на стыке участков ко­лонны различного сечения.

Таким образом, дополнив алгоритм расчета колебаний ко­лонны бурильных труб (см. главу 2, § 3) уравнениями (4.8), (4.15) — (4.18), описывающими соотношение деформаций в ме­стах установки преобразующих устройств, можно проанализи­ровать влияние этих устройств на показатели процесса разру­шения забоя. В качестве примера приведем зависимости скорости проходки от параметров амортизирующего устройства и места его установки, рассчитанные для простейшего случая моделирования долота одновенечным зубчатым катком. Напом­

ним, что при таком способе моделирования все явления, свя­занные с колебательными процессами, проявляются в полной мере, в то время как при полном моделировании конструкции и кинематики долота эти эффекты в значительной степени сгла­живаются вследствие несинхронное™ работы отдельных венцов. Расчет производился для компоновки, включающей 100 м УБТ причем было принято, что в сечении раздела УБТ и НБТ про­исходит отражение энергии упругих волн.

Рис. 44. Расчетная зависимость скорости проходки от места установки пружинного аморти­затора

Рис. 43. Расчетная зависимость скорости проходки от жестко­сти пружинного амортизатора

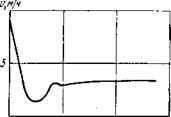
На рис. 43 представлена зависимость скорости проходки от жесткости амортизатора, установленного непосредственно» над долотом. В данном примере, начиная с жесткости 700 кге/мм, амортизатор практически перестает оказывать влия­ние на скорость бурения и долото работает как при жесткой компоновке. При меньшей жесткости скорость бурения суще­ственно увеличивается. Нужно учесть, что увеличение скорости достигается за счет высокочастотных вибраций долота, которые могут представлять опасность для прочности его конструкции.

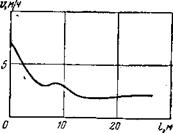
На рис. 44 показана зависимость скорости проходки от места установки пружинного амортизатора. Эта зависимость имеет довольно сложный характер, однако при увеличении расстоя­ния от амортизатора до долота свыше 10 м он перестает ока­зывать влияние на скорость бурения.

Аналогично были проведены расчеты для резинового амор­тизатора, причем полученные зависимости носят примерно такой же характер, как и для пружинного (рис. 45 и 46).

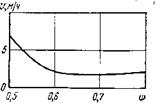
Расчетная проверка влияния скорости вращения долота на эффект действия амортизаторов показала, что пружинный амор­тизатор может вызывать ряд экстремальных значений скорости проходки, носящих явно выраженный резонансный характер. Что касается резинового амортизатора, то в этом случае был обнаружен для рассмотренного конкретного примера единствен­ный минимум в области низких оборотов.

Рис. 46. Расчетная зависимость скорости проходки от места установки резинового аморти­затора

цм)ч Рис. 45. Расчетная зависи­мость скорости проходки от коэффициента поглощения резинового амортизатора

Приведенный пример отнюдь не претендует на получение универсальных зависимостей, касающихся влияния амортизи­рующих устройств на эффективность процесса бурения. Однако он показывает, что устройства, преобразующие и поглощающие энергию упругих волн, могут оказывать весьма существенное и иногда неожиданное влияние на процесс бурения. Поэтому метод математического моделирования может оказать неоце­нимую помощь при проектировании механизмов, входящих в компоновку низа бурильной колонны, и в прогнозировании «ожидаемых показателей эффективности бурения.

Комментарии запрещены.