Бурение грунтовых зондов, установка энергетических колодцев

При проектировании шарошечных долот одной из важных: проблем является вопрос выбора шага зубцов на каждом из венцов шарошек долота. Разработанная нами математическая модель процесса бурения позволяет исследовать влияние изме­нения шага зубцов на венцах шарошек на максимальное внед­рение зубцов долота в породу и механическую скорость бурения..

При этом, не прибегая к конструированию и изготовлению1 долот, можно оценить это влияние в достаточно широком диа­пазоне изменения конструктивных параметров долота.

К задаче о влиянии шага зубцов на показатели разрушения можно подойти двояко. Во-первых, можно попытаться иссле­довать зависимость этих показателей от количества зубцов на каждом венце всех трех шарошек долота или на группах венцов, например периферийных. Во-вторых, интересно оценить влияние общего количества зубцов на всем долоте в целом. Эта по­следняя задача касается вопроса о сравнительной эффектив­ности работы долот с различной плотностью вооружения.

Такие задачи могут решаться для конкретных случаев при проектировании долот, предназначенных для разбуривания опре­деленных интервалов, или при выборе наиболее подходящего типа долота. Для расчетов используется вариант модели, в котором моделируются конические шарошки и отдельно каждый венец. Опыт подобных расчетов показывает, что при сопоста­вимых режимных параметрах общий вид зависимости для различных долот. имеет сходный характер. Поэтому продемон­стрируем получающиеся расчетные зависимости на примере •трехшарошечного долота диаметром 214 мм при разбуривании известняков верхнего карбона, встречающихся на месторожде­ниях Волго-Уральского региона.

При изменении количества зубцов на одном или нескольких венцах, на других венцах шарошек сохранялось базовое коли­чество зубцов, соответствующее конструкции моделируемого серийного долота, представленное ниже.

Номер шарошки……………………………………………. 1………………… 2 3

Количество зубцов 5 6 23 10 19 21 13 22 22

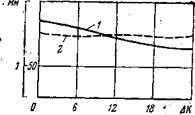
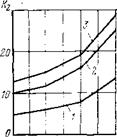
4л№ Цм/ч Рис. 50. Расчетные зависимости глубины внедрения зубцов (/) и скорости проходки (2) от измене­ния числа зубцов на третьих вен­цах шарошек

Для расчетов были использованы лабораторные зависимости P(z) и V(z), полученные при условиях фактического залегания для разных скоростей соударения зубцов с породой.

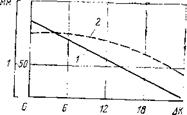
?ш. цм/ч Рис. 49. Расчетные зависимости глубины внедрения зубцов (1) и скорости проходки (2) от изме­нения числа зубцов на третьем венце третьей шарошки

На рис. 49—52 представлены зависимости изменения глу­бины максимального внедрения зубцов долота в породу и ско­рости бурения v от числа зубцов на венцах шарошек при нагрузке на долото G = 20 тс и скорости вращения п = = 1000 об/мин. Число зубцов К на венцах варьировалось сле­дующим образом: на первых венцах от 6 до 20, на вторых — от 10 до 30, на третьих — от 15 до 35. При расчете количество зубцов на каждом венце увеличивалось от нижнего урозня до верхнего.

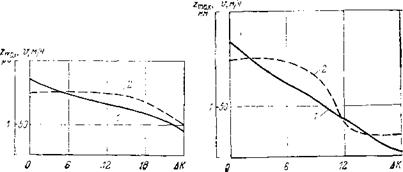
Рис. 51. Расчетные зависимости глубины внедрения зубцов (1) и скорости проходки (2) от изменения числа зубцов на вто­рых венцах шарошек

Рис. 52. Расчетные зависимости глу­бины внедрения зубцов (1) и скоро­сти проходки (2) от изменения числа зубцов на вторых и третьих венцах шарошек (£7=20 тс)

На графиках зависимостей показателей разрушения от числа зубцов по оси абсцисс отложено приращение АК от нижнего уровня К lain — Предполагается, что на всех аналогичных венцах трех шарошек количество зубцов отличается на два.

Так, например, на рис. 52 цифра 12 на оси абсцисс означает, что к исходному нижнему уровню на вторых венцах шарошек •Kmm=10 прибавлено соответственно: на первой шарошке 10 зуб­цов, на второй — 12 и на третьей—14. То же количество при­бавлено на третьих венцах к исходному уровню /Стш=15. Сле­довательно для этой точки на графике количество зубцов на вторых венцах будет — 20, 22, 24, а на третьих — 25, 27, 29.

Увеличение количества зубцов на одном из венцов (см. рис. 49) одной шарошки долота, как правило, приводит к весьма незначительному уменьшению углубления зубцов в породу. Ме­ханическая скорость проходки практически остается неизменной. Вообще, влияние шага или количества зубцов-яа скорость буре­ния проявляется слабее, чем на углубление зубцов. Это объяс­няется тем, что с увеличением шага отдельные удары становятся более эффективными, но зато количество их в единицу времени уменьшается. Поэтому возможны случаи, когда при увеличении шага зубцов скорость бурения даже несколько снижается. Не­маловажно также определенное сочетание нагрузки на долото и количества зубцов на нем. При недостаточной нагрузке ука­занный выше характер зависимости может измениться.

При соответствующем изменении числа зубцов одновременно на всех третьих венцах шарошек или одновременно на всех вторых венцах характер зависимости сохраняется, но изменение показателей процесса разрушения оказывается более сущест­венным. Еще более сильное влияние оказывает одновременное изменение зубцов на вторых и третьих венцах всех шарошек.

Если изменение количества зубцов на третьем венце одной из шарошек от нижнего уровня до верхнего изменяет 2тах прибли­зительно на 25% и практически не изменяет механической скорости, то аналогичное изменение на всех вторых и третьих венцах снижает 2тах более чем в 3 раза, а скорость бурения — более чем вдвое.

Интересно, что зависимость zmSLX(&K) имеет характер, близ­кий к линейному. Характер влияния АЛ на скорость бурения значительно более сложный. Например, увеличение числа зуб­цов на вторых и третьих венцах до определенного предела (на вторых венцах от 10 до 18—20 и на третьих — от 15 до 22—24) практически не влияет на скорость бурения. При одновремен­ном изменении числа зубцов на вторых и третьих венцах всех шарошек резкое изменение механической скорости происходит в диапазоне изменения числа зубцов в среднем на вторых вен­цах от 17 до 22 и на третьих ■— от 22 до 27.

Физическое объяснение влияния шага между зубцами на величину максимального углубления их и, следовательно, на скорость бурения заключается в следующем. При увеличении шага величина углубления должна расти из чисто геометриче­ских соображений. Однако темп этого роста зависит от харак­тера зависимости P(z). Чем меньше растет сопротивление по­роды по мере увеличения глубины внедрения зубцов, тем интен­сивнее влияние шага на максимальную глубину внедрения. Действительно, при резком нарастании сопротивляемости по­роды с глубиной геометрический эффект увеличения шага пой­дет главным образом на подъем нижнего сечения колонны. Для известняка верхнего карбона как раз характерен незначи­тельный прирост усилия от скачка к скачку, поэтому априори следует ожидать благоприятного влияния уменьшения числа. зубцов на максимальное их углубление и на скорость бурения. Для породы с более резко нарастающим сопротивлением меха­ническая скорость может даже уменьшаться за счет сокраще­ния общего количества ударов.

Разумеется, полученные данные действительны для одного определенного сочетания нагрузки на долото и свойств породы. При изменении нагрузки и прочности породы результаты иссле­дования могут получиться иными.

Так, например, при нагрузке 10 тс, не всегда обеспечиваю­щей объемное разрушение породы, оказалось, что влияние изме­нения числа зубцов на вторых и третьих венцах шарошек в тех же пределах обеспечивает zmax несколько менее чем в 3 раза. Зато характер влияния АЛ на скорость бурения совершенно иной, чем при нагрузке 20 тс.

Это происходит потому, что увеличение значения 2тах, кото­рое имеет место при уменьшении количества зубцов на венцах шарошек, все же не столь значительно и не имеет линейного характера, как при нагрузке 20 тс, и не гасится за счет сокра­
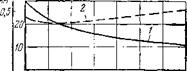
щения общего количества ударов в единицу времени. Кроме того, расчет скорости ведется по начальному участку кривой V(z), где разрушаемые объемы породы весьма малы. На рис. 53 приведены графики изменения гтах и и с изменением числа зубцов. Механическая скорость увеличивается незначи­тельно и даже достигает максимума при наибольшем числе зубцов на венцах шарошек.

О Ь 8 12 16 20 — 22 АК

Выше рассмотрено влияние количества зубцов на отдельных венцах и на группах венцов на показатели процесса разруше­ния. Однако при конструировании шарошечных долот сущест­вуют определенные принципы, не позволяющие произвольно и независимо друг от друга выбирать количество зубцов на отдельных венцах. Попытаемся поэтому произвести оценку? пш, v. m/ч

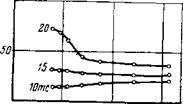
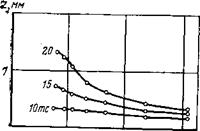
Рис. 53. Расчетные зависимости глубины внедрения зубцов (1) и скорости проходки (2) от измене­ния числа зубцов на вторых и третьих венцах шарошек (G — = 10 тс)

влияния общей плотности вооружения на долоте. С этой целью для долота диаметром 214 мм было просчитано семь различных вариантов комбинаций числа зубцов на девяти венцах трех шарошек долота (табл. 11). За базу принят один из серийных

Таблица 11

Номер вариан* та	1-я шарошка	2	-я шарошка	3	-я шарошка	Суммарное число зубцов на долоте
1-й венед	2-й венец	3-й венец	1-й венец I	sr о § С4!	3-й венец	1-й венец	2-й венец	1 3-й венец
1	5	8	12	5	10	13	8	14	14	89′
2	5	9	13	5	11	14	8	15	15	95
3	5	10	14	6	12	15	9	16	16	103
4	5	12	16	7	14	17	10	18	18	117
5	5	14	18	8	16	19	11	20	20	131
6	5	19	23	11	21	24	14	25	25	167
7	5	24	28	14	26	29	17	30	30	203

вариантов долота, который в таблице соответствует пятому варианту.

Для иллюстрации на рис. 54 представлены варианты чисел зубцов на венцах второй шарошки.

Результаты расчета величин углублений зубцов в породу и соответствующих механических скоростей бурения для указан­ных семи вариантов при трех различных осевых нагрузках на долото представлены на рис. 55 и 56.

Анализируя результаты, можно сде­лать следующие заключения:

1 Z 3 V 5 6 7 N° варианта Рис. 54. Варианты варьирования чис­ла зубцов на вен­цах второй шарош­ки при расчетах на ЭВМ: 1— 1-й венеа: 2— 2-ffc венед; 3 — 3-й венец.

— функция механической скорости от общего количества зубцов на долоте количественно и качественно зависит от величины осевой нагрузки;

— характер этой зависимости суще­ственно нелинейный;

— при нагрузке, достаточной для объ­емного разрушения, механическая ско­рость резко возрастает при снижении об­щего числа зубцов менее 120;

— при меньших нагрузках уменьше­ние количества зубцов либо вовсе не влияет на механическую скорость, либо даже снижает ее;

v, m/4

—■ с точки зрения механической ско­рости для бурения известняков средней твердости при недостаточных нагрузках выбор типа долота существенной роли не играет.

о 1Р0 150 к 0 100 150 а

Рис. 55. Расчетная зависимость глу — Рис. 56. Расчетная зависимость ско — бины внедрения зубцов от измене — рости проходки от изменения общего ния общего количества зубцов на до — количества зубцов на долоте лоте

Приведенные данные показывают, что разработанная мето­дика дает гораздо большие возможности для проектирования вооружения долот, чем непосредственный анализ результатов; разрушения пород единичными зубцами.

Предложенный выше метод выбора оптимального количества — зубцов на венцах шарошечного долота обладает тем недостат­ком, что выбор рассматриваемых вариантов не является доста­точно обоснованным и систематичным. Поэтому в ряде случаев, целесообразно воспользоваться теорией планирования экстре­мальных экспериментов. Согласно этой теории можно при
проведении минимального количества экспериментов построить уравнение регрессии, оценить значимость исследуемых факторов ■и определить направление и шаг движения по градиенту к об­ласти оптимальных вариантов, т. е. к области цтах-

Вместо физических экспериментов для определения коэффи­циентов уравнения регрессии будем пользоваться расчетными экспериментами с помощью математической модели процесса бурения.

Зададимся простейшим вариантом линейной модели функции v = f(Xi) с учетом эффектов взаимодействия

TOC o "1-5" h z П П

V = а0 + Л aiXi + J} aijxixj — (5-1)

t «■/

Здесь использованы обозначения, общепринятые в теории планирования эксперимента: а0, т, — коэффициенты урав­нения регрессии; хц — исследуемые факторы, соответствующие числам зубцов на i-м и /-м венцах.

Если за независимые переменные (факторы) функции v = = f(X{) принять числа зубцов на девяти венцах шарошек, то минимальное число расчетных экспериментов, которое необхо­димо для получения указанной модели, составило бы 29=512, что практически трудно выполнимо. К тому же обычно при конструировании вооружения шарошечных долот плотности во­оружения на всех трех шарошках обычно мало отличаются друг ют друга, поэтому целесообразно использовать модель долота, имеющего три одинаковые шарошки. В этом случае число неза­висимых переменных (факторов) сокращается до трех (три венца) и число вариантов расчета модели процесса бурения сокращается до 23 = 8. Чтобы избежать синхронности в работе шарошек, следует задать различное начальное положение зуб­цов, контактирующих с породой. Использование такой схемы позволит, по-видимому, достаточно обоснованно выбрать опти­мальный вариант вооружения, внося в результаты расчетов соответствующие поправки. Для расчетов были выбраны кон­структивные параметры 2-й шарошки одного из вариантов се­рийного долота типа 214Т, уже использованного выше. Также, аналогично предыдущему, в качестве разбуриваемой породы были использованы известняки верхнего карбона.

Планирование экспериментов для получения линейной мо­дели с учетом факторов взаимодействия основано на варьиро­вании факторов на двух уровнях. Уровни варьирования факто­ров приведены в матрице планирования (табл. 12).

В соответствии с составленным планом проводились расчеты с помощью математической модели процесса бурения. Резуль­таты расчета представлены в той же табл. 12.

По найденным значениям величин и рассчитаны коэффи-

Уровни	Кодированные значения	1-й венец Х	Факторы 2-й венец *2	3-й венец *3	Зависимая пе­ременная
Верхний уровень	+i	20	30	35
Основной уровень	0	13	20	25
Нижний уровень	—1	б	10	15
Интервал варьирования		7	10	10
№ опыта 1		+	+	1 1	35,0
2		“Г	+		53,2
3		+	—	1	40,2
4		+	—		68,5
5		—	+	+	35,5
6		—	+	—	73,8
7		—		+	91,6
8			—	—	89,5

циенты соответствующего уравнения регрессии и = /(Х, Хг, Хз) в кодированном виде

v = 60,90 — 11,69xj — 11 ,53х2 — 10,ЗЗх3 — f 6,42х1х2 — 1,29х1х3 — — З,77х2х3 + 6,32х1х2х3. (5.2)

Чтобы провести оценку значимости коэффициентов в урав­нении (5.2), нужно определить дисперсию воспроизводимости, расчетного эксперимента.

Мера отклонения искомой функции от среднего значения определяется дисперсией исходных данных. В качестве исходной информации в модели задаются экспериментальные зависимости силы сопротивления породы от глубины внедрения зубца P(z) и объема разрушенной породы от глубины V(z), которые имеют разброс относительно их среднего уровня. Серии эксперимен­тальных зависимостей P(z) и V'(e), вводимые в модель, по­лучены при повторных экспериментах на одной породе и при одинаковых условиях. Вводя эти данные в модель, получаем: для каждого варианта разброс относительно приведенных в табл. 12 средних значений скорости бурения. Это позволяет по* известным формулам подсчитать дисперсию воспроизводимости и дисперсии коэффициентов регрессии.

Задавшись доверительной вероятностью, можно произвести, оценку значимости коэффициентов уравнения регрессии. Аде­кватность линейной модели проверяется сравнением свободного члена уравнения регрессии и значения скорости бурения на основном уровне, полученного путем дополнительного расчета по математической модели процесса бурения.

В результате указанных выше оценок оказалось, что урав­нение (5.2) может быть записано в следующем виде:

о = 60,90— 11,69^— 11,53*2— 10,33*3. (5.3)

Если пересчитать это уравнение для натуральных неполиро­ванных значений хи хг, хэ, то можно получить интерполяцион­ную формулу для оценочных расчетов скорости и при различных средних числах зубцов на венцах.

Установим, в какой мере каждый из факторов влияет на величину V. Величина коэффициента регрессии — количествен­ная мера этого влияния. Чем больше коэффициент, тем сильнее влияет фактор. Коэффициенты при факторах *ь х2, *з имеют близкие значения, и нетрудно убедиться, что изменения числа зубцов на 1-м, 2-м, 3-м венцах шарошки примерно одинаково влияют на максимальное углубление зубцов долота в породу.

О характере влияния факторов можно судить по знакам коэффициентов. Знак минус свидетельствует о том, что с уве­личением числа зубцов на каждом из венцов величина углуб­ления убывает. Для достижения максимума функции отклика /(*!, Х2, *з) увеличение всех факторов, имеющих знак минус, неблагоприятно.

Для отыскания оптимального варианта числа зубцов на венцах шарошек воспользуемся методом крутого восхождения по линейной поверхности отклика v = f(xu х2, *з). Этот метод позволяет определить область оптимума функции отклика, основываясь на линейном уравнении регрессии, даже в том случае, когда указанная зависимость в действительности более высокого порядка.

По коэффициентам уравнения регрессии определяем состав­ляющие полного градиента для независимых факторов *ь *2, *з. Для этого следует коэффициенты уравнения регрессии v = = /(* 1, х-2, *3) при факторах хи *2, *з умножить на интервалы варьирования этих факторов. *

= — 11,69-7 = — 81,83; flgy2 = — 11,53-10 = —115,30; a3J3 = — 10,33-10 = — 103,30.

После деления составляющих градиента на одно и то же наибольшее целое число и округления величины (—2; —3; —3) ■следует последовательно прибавлять к основному уровню (*i = = 13; *2 = 20; *з = 25).

Получим серию комбинаций чисел зубцов на трех венцах, при которых следует дополнительно провести расчеты скорости проходки по математической модели процесса бурения.

Реализации этих комбинаций представлены в табл. 13.

Так как при линейном моделировании оказалось, что макси­мум скорости проходки соответствует нижнему уровню факто-

Факторы	Реализация I	Реализация II	Реализация III	Нижний уро­вень
*1	11	9	7	6
*2	17	14	11	10
*3	22	19	16	15
	58,82	80,67	96,24	89,49

ров, т, е. минимальному количеству зубцов на веннах, то эти данные также приведены в табл. 13.

Как видно из Табл. 13, метод крутого восхождения по гра­диенту позволил определить другую комбинацию зубцов (реа­лизация Ш), при которой скорость бурения несколько выше.

Таким образом, определив направление градиента, уже нет надобности пользоваться линейной моделью и можно рассчитать натуральные значения v в соответствии с методом математи­ческого моделирования процесса бурения при небольшом числе комбинаций параметров. При этом оказалось, что оптимальные значения чисел зубцов отличаются от тех, которые соответст­вуют нижнему уровню. Таким образом, удается внести поправки в оптимальные значения параметров по сравнению с линейной моделью.

Разумеется, для расчета при других режимах бурения и для других пород коэффициенты уравнения v = f(xu х2, х3) и опти­мальные варианты могут быть иными. Описанный метод следует рассматривать как довольно быстрый способ выбора такого типа вооружения долота, который в заданных условиях позволит достигнуть наибольшей начальной скорости проходки.

Комментарии запрещены.