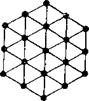
Взаимодействие зон разрушения при формировании забоя
Взаимодействие зон разрушения при формировании забоя
В предыдущих разделах были рассмотрены некоторые вопросы влияния конструктивных параметров трехшарошечных долот на показатели эффективности бурового процесса. При этом был заранее принят венцовый принцип размещения породоразрушающих элементов по рабочим поверхностям шарошек. Между тем нет никаких оснований априори считать, что размещение лунок разрушения на поверхности забоя концентрическими кольцами является оптимальным. Попытаемся подойти к этому вопросу, исходя исключительно из соображений достижения наиболее эффективного взаимодействия соседних зон разрушения между собой. Сущность такого подхода заключается в том, чтобы абстрагируясь временно от конкретной конструкции долота, исследовать взаимодействие лунок разрушения, образуемых зубцами различных конфигураций при их последовательном или одновременном внедрении в поверхность
разрушаемой породы. При работе обычного шарошечного долота имеют место оба этих варианта. При одновременном внедрении тензоры напряжений, образуемых соседними зубцами, соответствующим образом складываются, что приводит к возникновению своеобразной картины разрушения двойным или групповым индентором. При этом может измениться величина удельной нагрузки, необходимой для образования скачка разрушения. Зоны разрушения могут остаться независимыми или слиться между собой в зависимости от расстояния между ин — денторами, их размеров, конфигурации, взаимного расположения и ориентации.
Те же вопросы встают и при последовательной обработке поверхности породы. Разница заключается в том, что в этом варианте тензоры напряжений не взаимодействуют, а изменяются краевые условия задачи, так как очередной единичный индентор внедряется в полупространство с выемками от предшествующих взаимодействий.
Несмотря на принципиальную разницу одновременного и последовательного внедрения инденторов в поверхность породы, результаты взаимодействия оказываются схожими, поэтому в дальнейшем изложении они будут приведены главным образом для варианта одновременного внедрения инденторов.
Рассмотрим особенности напряженного состояния полупространства при вдавливании в него двух инденторов, представленных соответствующими эпюрами давления по поверхности контактных площадок.
Суммарное напряженное состояние рассчитывается на основе принципа аддитивности теории упругости с использованием методик расчета полей напряжений, возникающих от давления на контактные площадки различной конфигурации. Такие методики для круглых и прямоугольных площадок разработаны достаточно подробно [35, 36]. В этих методиках рассмотрены случаи равномерной и полусферической эпюр давления по круглой площадке, соответствующих вариантам вдавливания в поверхность породы круглых плоскодонных и полусферических инденторов, а также случаи равномерного давления на прямоугольную площадку с учетом радиуса скругления ее углов. Расчеты напряженных состояний полупространства во всех рассмотренных случаях ввиду их трудоемкости выполняются на ЭВМ. Не представляет принципиальной трудности составить программу расчета на ЭВМ напряженного состояния полупространства для произвольной эпюры давления, однако для целей общего анализа ситуации взаимодействия двух инденторов в этом нет надобности. Построение тензорного поля напряжений, возникающею от суммарного действия двух инденторов, позволило провести прочностной анализ объема породы, примыкающего к контактным площадкам. Это в свою очередь дает возможность установить зоны начала процесса разрушения, опре-
делить предполагаемый ход его развития и делать заключения «относительно конфигурации образующейся лунки и величины нагрузки, необходимой для осуществления различных стадий процесса разрушения.
Под прочностным анализом понимается расчет зон возникновения и развития остаточных деформаций в массиве породы [3, 36]. При проведении прочностного анализа используется обобщенный критерий прочности горных пород, основанный на построении поверхности предельных состояний по экспериментальным данным [36]. Прочностной анализ позволяет для каждого значения последовательно увеличивающегося давления на контактную площадку рассчитать для каждой точки полупространства, пребывает ли в ней порода в упругом состоянии или вышла из него. Таким образом, появляется возможность проследить за возникновением и развитием зон остаточных деформаций, которые могут быть представлены изолиниями постоянных давлений в сечениях полупространства.
В соответствии с поставленной задачей расчеты должны быть проведены для различных расстояний между осями индент оров.
Результаты расчета показывают, что при небольших расстояниях между инденторами образуется общее поле напряжений, в котором величина компонент напряжений в центральной плоскости между инденторами все же существенно ниже, чем под каждым из них в отдельности. При увеличении расстояния образуется независимая слабонапряженная зона в пространстве между инденторами. Наконец, при дальнейшем увеличении расстояния имеют место две отдельные независимые зоны напряжений. Таким образом, можно сделать заключение, что развитие процессов разрушения в начальный период происходит независимо под каждым из инденторов, даже когда они расположены весьма близко друг от друга.
Сравнение полей напряжений под изолированным инденто — ром [35] и индентором, действующим одновременно с соседним, показывает, что в последнем случае линии постоянных напряжений несколько отклоняются от оси симметрии во внешние стороны, как бы отталкиваясь друг от друга.
Интересно отметить, что все главные напряжения в центральной плоскости при небольшом расстоянии между инденторами являются отрицательными. Таким образом, ядро сжатия, примыкающее при вдавливании одного индентора непосредственно к площадке контакта, в случае двух инденторов распространяется на объем полупространства между ними. Поскольку ядро сжатия является областью, через которую затруднено прохождение магистральных трещин, можно предсказать, что в случае первого механизма разрушения [36], кони — ‘ ческие трещины будут развиваться во внешние стороны и лишь при большой нагрузке они сомкнутся между собой. Это пол
ностью подтверждается экспериментально при вдавливании двух цилиндрических инденторов в поверхность блока оптического стекла. При этом характерные конические трещины, начинающиеся от площадок контакта, развиваются преимущественно во внешнюю сторону, в то время как область между инден — торами остается для них как бы запретной, вплоть до весьма значительных нагрузок.
|
|
|
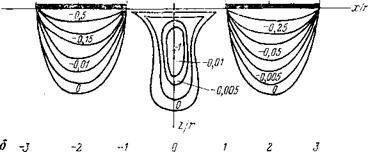
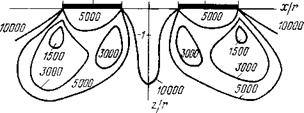
Рис. 57. Расчетное поле изобар главных нормальных напряжений при взаимодействии двух площадок давления: |
Все сказанное позволяет сделать вывод, что не приходится ожидать какой-либо эффективности процесса разрушения при взаимодействии полей напряжений двух одновременно внедряе-
а — площадки круглые, эпюра давления равномерная; б — площадки круглые, эпюра давления полусферическая; в — площадки прямоугольные, эпюра давления равномерная
мых инденторов. Напротив, они как бы препятствуют друг другу создавать разрушающие напряжения с внутренней стороны. Следовательно, необходимо рассмотреть вариант вдавливания инденторов при значительном расстоянии между ними, когда зоны предразрушения развиваются независимо и только на
|
|
|
5 — з -2 -1 О 7 2 J
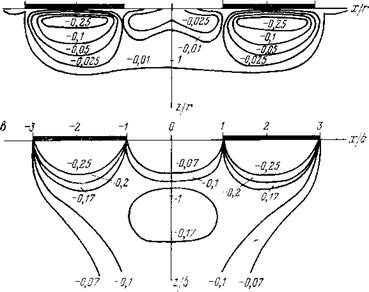
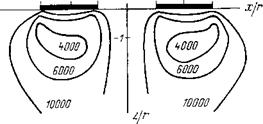
Рис. 58. Расчетное поле изохром при взаимодействии двух площадок давления: |
а площадки круглые, эпюра давления равномерная; б — площадки круглые, эпюра давления полусферическая; в — площадки прямоугольные, эпюра давления равномерная
заключительной стадии при формировании магистральных трещин выкола эти последние могут слиться между собой, образуя объединенную двойную лунку.
В качестве примера на рис. 57 и 58 приведены изобары наибольших главных нормальных напряжений ajp и изохромы Ттах/р Для площадок контакта, образуемых цилиндрическими инденторами с плоской и полусферической вершиной, а также прямоугольными инденторами с площадкой контакта при отношении сторон ajb — Ъ при расположении их параллельно друг к другу длинными сторонами. Графики на рис. 57 и 58 даны в относительных величинах, где напряжения отнесены к текущему давлению на площадку контакта р, а координаты — соответственно к радиусу г плоскодонного индентора или сферы, или к половине ширины прямоугольной площадки контакта b при относительном расстоянии между осями инденторов х/г = = х/Ь = 4.
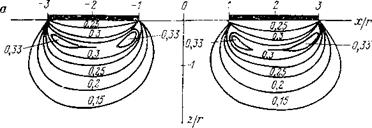
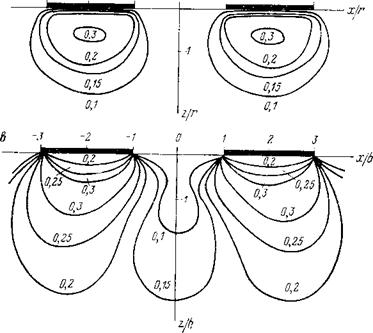
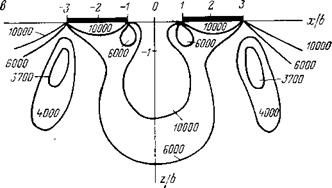
Изучение расчетных зон остаточных напряжений при различных нагрузках подтверждает сделанные выше выводы и дает основание для некоторых дополнительных заключений. На рис. 59 представлены зоны остаточных деформаций для трех перечисленных выше площадок контакта. Так же, как и изобары oi/p, они отклоняются от оси симметрии во внешние стороны. Это явление можно наблюдать экспериментально при просвечивании тонкой пластинки породы, вырезанной в плоскости, включающей оси обоих инденторов. При этом зоны остаточных деформаций непрозрачны и хорошо видны на светлом фоне просвечиваемой пластинки.
Ввиду того, что объем породы близ плоскости симметрии между инденторами не захватывается зоной предразрушения даже при весьма значительных нагрузках, можно прогнозировать, что эта центральная часть породы при образовании совместной лунки должна выколоться целиком или в виде нескольких крупных кусков.
Исследование зон предразрушения также показывает, что глубина общей лунки разрушения и величина необходимой для этого разрушения нагрузки не зависят от расстояния между инденторами, пока оно обеспечивает общий выкол. Эта глубина примерно равна радиусу плоскодонного индентора или половине ширины площадки призматического индентора. Экспериментальные исследования профилограмм объединенных лунок вполне подтверждают сделанные выше выводы.
Что касается инденторов с полусферической вершиной, то благодаря непостоянству контактной площадки при изменении нагрузки имеются некоторые особенности при образовании зон предразрушения. Так, необходимая для начала зарождения этих зон нагрузка с увеличением расстояния между инденторами несколько возрастает.
Теоретический анализ, изложенный выше, позволил соста-
|
|
|
|
|
Рис. 59. Расчетные зоны остаточных деформаций для двух площадок давления: а — площадки круглые, эпюра давления равномерная; б — площадки круглые, эпюра давления полусферическая; в — площадки прямоугольные, эпюра давления равномерная |
вить общее представление о характере взаимодействия соседних зон разрушения. Однако он же показал, что поиски наиболее эффективных схем поражения забоя следует вести при таких расстояниях между инденторами, при которых зоны предразрушения развиваются фактически независимо. В то же время не представляется возможным исследовать процесс разрушения вплоть до образования магистральных трещин выкола расчетнотеоретическим путем. Отсюда вытекает необходимость при дальнейшем изучении поставленной задачи прибегнуть к экспериментальному методу.
Общий план экспериментальных исследований можно представить следующим образом. Прежде всего для инденторов каждой из исследуемых конфигураций необходимо изучить зависимость эффективности разрушения от расстояния между двумя вдавливаемыми инденторами и попытаться установить оптимальное значение этого расстояния. Затем следует проверить влияние на этот оптимум, выраженный в относительных величинах, абсолютных размеров инденторов. Это необходимо для того, чтобы получаемые выводы могли быть использованы для рекомендаций при проектировании вооружения бурового долота. Следующим этапом является исследование совместного действия группы инденторов, расположенных линейно и при других способах их взаимного расположения. В результате этих экспериментов нужно выбрать наиболее эффективный способ расположения инденторов или, иными словами, оптимальную схему поражения забоя. Наконец, следует проверить влияние некоторых факторов, например забойного давления и скорости взаимодействия инденторов с породой на правильность выбора оптимальной схемы.
Поскольку, как уже было указано, в реальных конструкциях долот взаимодействие инденторов может происходить одновременно или последовательно, то изложенный выше план должен быть выполнен для обоих этих вариантов.
Многочисленные эксперименты в соответствии с приведенным выше планом показали, что выбор оптимальной схемы поражения практически не зависит от свойств разрушаемой породы, от размеров инденторов, порядка их взаимодействия и различных забойных факторов. Разница заключается только в незначительных изменениях относительной величины оптимального расстояния между элементами схемы.
Ниже в качестве примера приведены некоторые результаты экспериментальных исследований, подтверждающие общие выводы относительно выбора оптимальных схем поражения забоя.
При исследовании первого вопроса — зависимости величины объема разрушенной породы от расстояния между инденторами — осуществлялось статическое вдавливание инденторов в образцы породы. Инденторы устанавливали на расстоянии с = 2г, 4г, 6г, Юг, 12г. Нагрузку на инденторы увеличивали до момента первого выкола, затем замеряли линейные размеры и объем лунок разрушения. Эксперименты повторялись 10—20 раз. При этом относительная погрешность е при доверительной вероятности а = 0,9 составляла 10—20%. Как для плоскодонных, так и для сферических инденторов было установлено, что при одновременном внедрении двух инденторов существует межцентровое расстояние, при котором достигается максимум разрушенного объема. Поскольку глубина лунки выкола не зависит от расстояния между инденторами, то объем разрушенной породы с увеличением межцентрового расстояния увеличивается до тех пор, пока существует взаимодействие. Здесь же следует отметить, что не удалось обнаружить заметного влияния межцентрового расстояния на величину нагрузки в момент первого выкола. Следовательно, величина А — —тг—, где п — количество
СД
инденторов в группе, может служить достаточно представительной характеристикой эффективности группового внедрения. Выигрыш в объеме в результате взаимодействия имеет место при Л> 1.
Аналогичные эксперименты были проведены для призматических инденторов с прямоугольной площадкой контакта. Призматический индентор, кроме величины контактной площадки, характеризуется еще соотношением ее сторон, что усложняет проведение исследований. О существенном влиянии этого фактора свидетельствует сравнение зон остаточных деформаций, рассчитанных для одинаковой удельной нагрузки, приложенной по равновеликим квадрату и прямоугольнику. Эти расчеты показали, что под квадратной площадкой зона деформации глубже и охватывает большую область, чем под прямоугольной. Эксперименты подтвердили этот вывод — объем породы, разрушенный квадратным индентором, в 1,6 раза больше объема, полученного при внедрении прямоугольного индентора. Таким образом, при подготовке рекомендаций для проектирования оптимальных схем поражения забоя призматическими зубцами следует учитывать не только расстояния между ними, но и соотношения сторон контактных площадок.
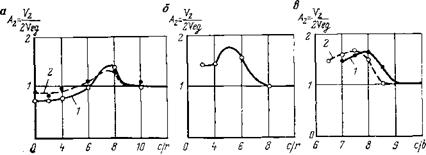
На рис. 60 приведены зависимости величины А2 = — 2 , ха-
ед
растеризующей величину объема совместного выкола по отношению к объему, образуемому двумя независимыми единичными выколами породы, от межцентрового расстояния. На рис. 60, а эти зависимости представлены для плоскодонных цилиндрических инденторов диаметром 2,5 и 5 мм. На рис. 60,6 — для цилиндрических инденторов с полусферической вершиной с радиусом сферы 2,6 мм и на рис. 60, в — для призматических инденторов с контактными площадками 5×1 и 10×2 мм. Приведенные графики показывают, что наблюдается четко выраженный максимум эффективности разрушения при оптимальном межцентровом расстоянии, которое составляет соответственно для цилиндрических плоскодонных инденторов около 8г, для цилиндрических инденторов с полусферической вершиной — при-
|
Рис. 60. Экспериментальные зависимости приведенного объема разрушения от относительного расстояния между инденторами: а—круглые плоскодонные инденторы: 1 — г=5, 2 — г=2,5 мм; б — инденторы с полусферической вершиной (г=2,6 мм); в — призматические инденторы: 1 — а=5, 6 = 1 мм; 2 — а=10, 6=2 мм |
близительно Ъг и для призматических инденторов 5X1 мм — 8b и 10X2 мм — 7,5Ь. Как видно из графиков, абсолютные размеры инденторов в определенных пределах практически не влияют на оптимальное межцентровое расстояние. При увеличении размеров инденторов наблюдается некоторое ослабление взаимодействия. Так, для плоскодонных инденторов диаметром 8 мм максимальное расстояние, при котором имеет место совместный выкол, а следовательно, и достигается наибольший объем разрушения, равно 7г.
При расположении призматических инденторов короткими сторонами, т. е. так, как это происходит при взаимодействии зубцов, расположенных на одной образующей шарошки, оказалось, что независимо от размеров инденторов оптимальное расстояние составило с = 9,5Ь, т. е. для инденторов 5×1 мм — 9,5 мм, для инденторов 10X2 мм—19 мм. Таким образом, наибольшая эффективность разрушения достигается при относительном расстоянии между венцами 4,56. Это обстоятельство весьма важно учитывать при разработке схем перекрытия забоя.
Итак, для всех рассмотренных конфигураций инденторов можно выбрать оптимальное расстояние между ними, при котором эффективность совместного разрушения оказывается наивысшей. Рассмотрим причину этого явления на примере взаимодействия плоскодонных цилиндрических инденторов. Из рис. 60, а видно, что при межцентровом расстоянии от 2г до 6г совместное вдавливание инденторов ведет к уменьшению разрушенного объема по сравнению с независимым вдавливанием. При расстоянии 6г объем разрушения тот же, что и при независимом вдавливании. И только при межцентровом расстоянии от 6г до 8г взаимодействие инденторов приводит к увеличению А> 1.
При малом расстоянии между инденторами зоны разрушения перекрывают друг друга, вследствие чего общий разрушенный объем уменьшается. При с = 6г поверхность разрушения близка к двум соприкасающимся кругам, радиусом 3г каждый. Этим и объясняется, что объем разрушения, приходящийся на каждый индентор, совпадает с объемом при единичном вдавливании. При увеличении расстояния с объем увеличивается непрерывно, вплоть до такого расстояния, при котором прекращается совместный выкол. Разумеется, результаты, представленные на рис. 60, являются среднестатистическими. При расстоянии с несколько больше оптимального в отдельных экспериментах объем разрушенной породы даже увеличивается. Однако в большинстве случаев совместного выкола не происходит. Поэтому средняя по совокупности величина объема резко сокращается. Этим объясняется несимметричный характер зависимостей А =
Рассмотрим теперь результаты взаимодействия зон разрушения при увеличении количества инденторов. Априори можно предположить, что при линейном расположении группы инденторов взаимодействие каждой пары соседних лунок практически не зависит от наличия остальных. Поэтому если рассматривать группу в делом, то объем разрушения, приходящийся на один индентор, зависит только от крайних лунок в ряду. Чем больше инденторов входит в линейную группу, тем меньше сказывается влияние крайних зон разрушения. Изложенное можно проиллюстрировать графиком зависимости относительного объема от общего количества взаимодействующих инденторов, размещенных на оптимальном расстоянии (рис. 61, а, кривая 1). Эта зависимость, приведенная для круглых плоскодонных инденторов, остается справедливой и для породоразрушающих элементов других конфигураций.
Для нелинейного расположения группы осесимметричных инденторов на поверхности разрушаемой породы возможны различные комбинации. Однако эксперименты показывают, что
|
|
|
|
|
Л |
|
7 |
|
7 |
|
13 |
|
1 л |
|
А Л “л пЛГа. |
Рис. 61. Экспериментальная зависимость (а) приведенного объема разрушения от количества инденторов:
1— линейное размещение инденторов; 2— размещение инденторов на плоскости (схема б)
наиболее эффективной является такая схема, в основе которой лежит равносторонний треугольник. Так, например, для четырех инденторов со сферической вершиной было проведено экспериментальное сравнение объема совместного выкола при размещении инденторов в вершинах квадрата и ромба, составленного из двух равносторонних треугольников. Оказалось, что во втором случае величина Л в 1,5 раза больше, чем в первом. Таким образом, группу осесимметричных инденторов следует размещать так, чтобы каждый из них располагался в центре правильного шестиугольника со стороной, равной наибольшему расстоянию совместного выкола. Заметим, что при этом оптимальное расстояние между инденторами оказывается несколько большим, чем при линейном их расположении.
На рис. 61, а (кривая 2) приведены результаты экспериментов по вдавливанию групп плоскодонных инденторов, состоящих из трех, семи, девятнадцати элементов (рис. 61,6). Из графика следует, что нелинейное расположение инденторов имеет значительное преимущество по эффективности разрушения. С увеличением общего количества инденторов в группе эффективность их взаимодействия возрастает, так как уменьшается относительное количество внешних инденторов. Однако еще при 19 инденторах кривая продолжает возрастать. Интересно попытаться сделать оценку объема, приходящегося на внутренние инденторы группы. Для этого нужно экспериментально определить объем разрушенной породы, приходящийся на индентор, расположенный в центре шестиугольника. Оказалось, что величина А в этом случае достигает 3,5. Эту величину можно принять за максимальное увеличение объема породы, разрушенной плоскодонными цилиндрическими инденторами, по сравнению с результатами единичного вдавливания. Для цилиндрических инденторов с полусферической вершиной эффект группового разрушения оказывается еще более значительным. Что касается инденторов с прямоугольной площадкой притупления, то их линейное расположение приводит качественно к тем же результатам, что и для осесимметричных инденторов. Другие варианты размещения связаны с вопросом взаимной ориентации прямоугольных площадок.
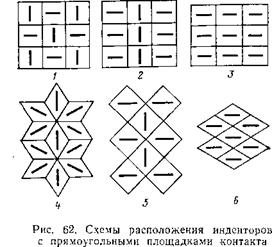
Способы такой ориентации могут быть весьма различными. На рис. 62 представлены шесть возможных схем размещения контактных площадок инденторов. Эти варианты хотя и не исчерпывают всех принципиальных возможностей размещения, но представляют их с полнотой, достаточной для практического использования. Простейшие схемы (1 и 2) основаны на параллельном размещении площадок в прямоугольном и шахматном порядках. Схемы 3 и 4 содержат последовательные ряды взаимно перпендикулярных площадок. В схеме 5 расположение площадок чередуется не только от ряда к ряду, но и в каждом ряду от индентора к индентору. Наконец, в схеме 6 предусмот-
|
|
рено расположение площадок, имитирующее размещение осесимметричных инденторов на рис. 61,6. Очевидно, что каждый индентор, входящий в схему, ответствен за разрушение участка поверхности, представленного на рис. 62 ячейками. Размеры ячейки устанавливаются экспериментально, т. е. определяется максимальный шаг между инденторами, обеспечивающий при первом скачке разрушения полное слияние соседних зон и образование целиком разрушенного участка породы со сравнительно ровным дном. При обеспечении такого размещения слой породы снимается с забоя при первом контакте с породоразрушающим инструментом.
Для сравнительной оценки предложенных схем может служить площадь ячейки, разрушаемой одним индентором, поскольку экспериментально установлено, что глубина разрушения с достаточной точностью оказывается одинаковой для всех испытанных вариантов. Поэтому требуется экспериментально определить наибольшие расстояния между рядами и между площадками в каждом ряду, обеспечивающие полный совместный выкол породы. Разумеется, эти расстояния оказываются различными для каждой схемы при одинаковых абсолютных размерах самих площадок. Сравнение площадей ячеек для различных схем показывает, что они оказались одинаковыми для третьей и пятой схем, а также для первой, второй и шестой. Если принять размер площадки первой, второй и шестой схем за единицу, то для третьей и пятой схем она окажется равной 1,1, а для четвертой схемы — около 1,5. Таким образом, оптимальным вариантом является чередование рядов перпендикулярно расположенных инденторов, причем инденторы соседних рядов расположены в шахматном порядке.
Изложенное выше показывает, что разработанная методика — сравнительной оценки различных схем поражения забоя позволяет осуществить обоснованный выбор принципа размещения породоразрушающих элементов на рабочих поверхностях долота. Этот принцип базируется на стремлении достигнуть таких условий бурения, при которых слой породы снимается за один оборот долота или за один контакт безопорного инструмента с забоем.
Заметим, что вопрос об абсолютных размерах породоразрушающих инденторов, образующих выбранную схему разрушения забоя, остается, вообще говоря, открытым. Он решается на основании конструктивных ограничений и сравнения показателей эффективности бурения, которые могут быть достигнуты при допустимом изменении размеров зубцов или штырей при заданной максимальной величине осевой нагрузки на долото.
Предложенная выше методика построения оптимальной схемы поражения забоя была изложена выше лишь принципиально. Очевидно, что на нее оказывают определенное влияние конкретные условия разрушения. Таковыми являются в первую — очередь забойное давление, скорость взаимодействия инденторов с породой, фактическая глубина внедрения инденторов в породу и последовательность их взаимодействия с забоем.
|
Л |
55555 |
|
к |
|
с/гопт>Фот |
|
10 |
|
|
|
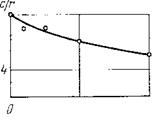
Рис. 63. Экспериментальные зависимости оптимального расстояния между инденторами от всестороннего давления (а) и глубины внедрения (б): 1 — три цилиндрических плоскодонных индентора (г=2,5 мм,, расположены треугольником); 2 — два призматических индентора (а=5, Ь = мм) |
|
500 р, кгс/см2 1 Z гтц, мм |
Рассмотрим эти вопросы несколько подробнее. С увеличением всестороннего давления диаметр лунки разрушения для единичного индентора уменьшается. Можно предположить, что будет уменьшаться и наибольшее расстояние между инденторами, при котором возможен совместный выкол. В самом деле,, экспериментальная проверка подтверждает это предположение. Существенными для некоторых пород также являются и параметры промывочной жидкости. На рис. 63, а приведена зави
симость оптимального расстояния между круглыми плоскодонными инденторами, расположенными в вершинах правильного равностороннего треугольника, от всестороннего давления раствора. Таким образом, забойные условия могут привести к необходимости некоторого сближения породоразрушающих инденторов.
Вполне очевидно, что при реальном процессе бурения глубина максимального внедрения зубцов в породу может быть различной и необязательно строго соответствовать осуществлению первого скачка разрушения. При изменении этой глубины, по-видимому, должно меняться также и оптимальное расстояние между инденторами, обеспечивающее совместный выкол. Ясно, что чем больше глубина внедрения зубцов, тем шире они должны быть расставлены. Эксперименты были поставлены для групп из трех плоскодонных цилиндрических и двух призматических инденторов (рис. 63, б). Таким образом, плотность вооружения долота зависит от расчетной глубины внедрения породоразрушающих элементов.
Что касается влияния скорости взаимодействия инденторов с породой на величину оптимального расстояния, то экспериментальные исследования, как правило, не показывают существования значимой зависимости от этого фактора.
В заключение рассмотрим взаимодействие инденторов при вдавливании со смещением во времени, т. е. когда последующий индентор производит разрушение вблизи лунки, образованной предыдущей. Многочисленные эксперименты показывают, что и для инденторов различных конфигураций общая закономерность сводится к тому, что не только оптимальное межцентровое — расстояние уменьшается, но и сокращается выигрыш в объеме разрушенной породы за счет взаимодействия соседних лунок. Сила же, необходимая для осуществления скачка разрушения, остается практически неизменной. Только при очень малых межцентровых расстояниях, т. е. когда очередное вдавливание производится по краю предыдущей лунки, наблюдается незначительное уменьшение нагрузки, вероятно, за счет уменьшения прочности породы в районе зоны разрушения.
Так, для плоскодонных цилиндрических и призматических инденторов при последовательном их действии оптимальное межцентровое расстояние уменьшается приблизительно с 8г до 6,5г и соответственно с 8b (для зубца 5X1) до 6,5 Ь.
Приведенные выше материалы показывают, что при использовании методики выбора оптимальных схем разрушения забоя для практического конструирования вооружения долот лабораторные испытания для выбранных пород необходимо выполнять в условиях, соответствующих фактическому разбуриванию с учетом забойных параметров, способа и режима бурения и принципиальной конструкции долота.
При использовании приведенных выше схем поражения за
боя для конструирования традиционных шарошечных долот с самоочищающимися венцовыми шарошками могут быть непосредственно применены лишь некоторые из них. При этом схемы разбиваются на отдельные элементы, последовательно осуществляемые различными шарошками. В силу независимости взаимного расположения зубцов разных шарошек трудно в точности воспроизвести заданную картину поражения забоя. Это ставит серьезную конструкторскую задачу о реализации кинематической связи между шарошками. Другая возможность заключается в использовании шарошек несамоочищающегося типа, для которых полного разрушения забоя при соответствующей нагрузке можно достичь при одной трети оборота долота. Для этого на каждой шарошке должны присутствовать все элементы используемой схемы. Разумеется, при этом необходимо внести поправки на непараллельное расположение зубцов ка соседних образующих конусов.
Однако материалы, приведенные в настоящем разделе, имеют значение не только для разработки принципиально новых схем вооружения. Весьма существенным является сам факт возможности использования эффекта взаимодействия соседних зон разрушения для интенсификации процесса бурения. В предыдущем разделе было показано, что с помощью математического моделирования можно выбрать оптимальное сочетание шага зубцов на венцах шарошек с нагрузкой на долото. При этом, однако, механическая скорость рассчитывалась без учета фактора взаимодействия соседних лунок. Теперь можно утверждать, что в определенном диапазоне изменения шага на каждом венце следует внести поправки на это взаимодействие, что приведет к возникновению локальных максимумов на зависимостях механической скорости от шага зубцов. Имеется полная возможность сравнить величину этого максимума с наибольшей скоростью, достигаемой при значительной величине шага, когда эффективное взаимодействие, по-видимому, отсутствует. Иными словами, можно установить для данных условий бурения, какой вариант предпочтительнее: выбрать шаг зубцов, обеспечивающий наибольшую эффективность каждого отдельного удара, или такой, при котором эта эффективность достигается за счет взаимодействия зон разрушения.