Бурение грунтовых зондов, установка энергетических колодцев

Одна из первых эмпирических формул была предложена в 1949 г. и основывалась на имевшихся данных Г. М. Шахмалнева об устье­вых температурах ряда бурящихся скважнп, а также на анализе кривых изменения температуры глинистого раствора с глубиной бурящейся скважины, построенных для восьми скважин района Сураханы. Температуру замеряли, спустя один день после цементи­рования обсадной колонны для определения высоты подъема цемента в затрубном пространстве скважины. Когда появились новые данные о температурных наблюдениях в бурящихся скважинах, эта фор­мула была уточнена (были определены значения входящих в нее опытных коэффициентов [22, 24 и др. 1).

За основу вывода указанной формулы были приняты положения, вытекающие из анализа промысловых замеров температуры цир­кулирующего раствора в буровых скважинах, расположенных на различных площадях.

Без особой погрешности можно принять, что в процессе бурения скважин температура циркулирующего глинистого раствора распре­деляется по закону прямой. При этом данная прямая располагается круче лилии температуры пород и пересекает ее таким образом, что ниже топки пересечения (считая от забоя скважины) температура раствора всегда меньше температуры пород, а выше этой точки — больше температуры пород.

Отсюда следует, что пельзя определять забойную температуру циркулирующего раствора, исходя только из значений геотермиче­ского градиента.

С возрастанием глубины скважины прямая температуры цир­кулирующего глинистого раствора как бы скользит вниз, парал­лельно самой себе. Это означает, что при всех прочих равпых усло­виях в двух или нескольких скважинах, имеющих различную глу­бину^ температура циркулирующего раствора на какой-либо глу­бине А, одинаковой для всех этих скважин, будет различной и тем большей, чем больше глубина забоя скважины Н.

В скважинах, расположенных на одном поле данной площади и имеющих одинаковую глубину, температура циркулирующего раствора во всех точках, расположен­ных на одинаковых глубинах, будет одинаковой. С увеличением глубины скважины температура циркуляру — н ющего раствора па забое и устье уве­личивается на одинаковую величину; при атом чем глубже скважина, тем больше должна быть разность между забойной температурой раствора и тем­пературой пород.

С некоторым допущением характер изменения забойной температуры цнр-f

кулирующего раствора в зависимости

от глубины может быть выражен для _________ ^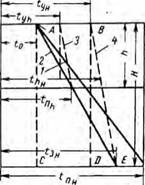

любой скважины прямой, имеющей „ „

, г Рис. 31. Схема распределения

вначале (на устье) одну общую точку температури по стволу буря-

с линией температуры пород, а на забое щеися скважины.

достаточно далеко от нее отстающей.

С прекращением циркуляции раствор, находящийся в нижней части скважипы (до точки пересечения указанных выше прямых), начнет нагреваться, а в верхней ее части охлаждаться, стремясь установить по всему стволу температуру, соответствующую темпера­туре пород.

При этом, однако, необходимо иметь в виду, что для каждой скважипы величина углового коэффициента прямой будет различной.

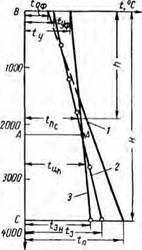
Обобщая и схематизируя сказанное, построим в прямоугольных координатах Н — t (рис. 31) все линии температур; температуры пластов 1, забойных температур циркулирующего раствора 2, рас­пределения температур циркулирующего раствора по стволу сква­жин, имеющих забои па глубинах h и Н, 3 н 4,

Отрезок, отсекаемый линиями 1 и 2 на оси температур, будет представлять собой некоторую постоянную температуру, которую обозначим через t0. Отрезок на той же оси температур, отсекаемый линией 4, соответствует температуре раствора, выходящего из устья скважины, имеющей забой II. Эту температуру обозначим че­рез t. Максимальную температуру циркулирующего раствора

на забое той же скважины обозначим через а температуру пород (пласта) на той же глубине Я через tng.

Опуская из точки А перпендикуляр, получим два прямоуголь­ных треугольника АСЕ и ACF, рассмотрев которые получим сле­дующие зависимости:

(VI.20)

н

,1Я-<0 -‘eP-G <«н «-£- + *. (VI.21)

Первая из этих зависимостей представляет собой общеизвестное выражение, температуры пластов на основе геотермического градиента (геотермической ступени); вторая позволяет определить максималь­ную температуру циркулирующего раствора па забое при глубине Н. Определить температуру раствора на другой глубине скважины по этой формуле нельзя. Формула (VI.21) не дает возможности устано­вить распределение температуры циркулирующего раствора по стволу бурящейся скважины, поэтому имеет ограниченное примене­ние.

Можно вывести зависимость, пригодную для более общего слу­чая. Для этого достаточно рассмотреть прямоугольный треугольник DBE, из которого следует, что

-ф-=геу-с /.a~f(VI.22)

или определить в более общем случае температуру раствора в точке, соответствующей некоторой глубине h скважины общей глубиной Я:

h =tg Y = C, + (VI.23)

г*Н ТН е га

Обозпачив а = —, окончательно получим

tka=ah + t1B. (VI.24)

Найденная зависимость дает возможность определить темпера­туру циркулирующего раствора в любой точке ствола скважины. Для этого необходимо знать коэффициент а и температуру раствора на устье t д, соответствующую глубине скважины Я.

Как удалось установить, устьевую температуру раствора можно увязать с глубиной скважины зависимостью вида:

*Ш=*04-ЬЯ, (VI.25)

где b — некоторый опытный коэффициент.

Эта зависимость упрощает задачу. Если в формулу (VI.24) под­ставить вместо величины ljg ее значение из выражения (VI.25),

tkJI = ah+bH + t0. (VI.26)

Чтобы пользоваться этим выражением, достаточно зпать глубину скважины и значения коэффициентов а и Ъ. Однако эти коэффициенты могут быть найдены только при непосредственных наблюдениях.

Полученпые значения коэффициентов а и b для различных неф­тяных районов и площадей приведены ниже.

По данным этой таблицы средние значения коэффициентов а и Ь равны соответственно 0,00357 и 0,00867.

Площадь	Коэффициент
а	Ь
Зыря……………………………………………………………….	0,00385-0,00308	0,0074
Гоусаны………………………………………………………….	0,00435-0,00345	0,0081
Биби-Эйбат. …… ……………………………………………..	0,0040	0,0092
Карадаг………………………………………………………….	0,0027	0,0100

Использование приведенных значений коэффициентов а и b дает возможность применить зависимость (VI.26) для практических целей, причем при ориентировочных расчетах можно принять, что

t„H = 0,004/1 + 0,0085Я + 14,5. (VI. 26а)

Для определения температуры циркулирующей промывочной жидкости ряд эмпирических зависимостей предложил Ф. Н. Фомен­ко, исходя из результатов наблюдений в скв. 216 площади Лок — Батаи, где замеряли устьевые и забойные температуры глинистого раствора. В результате этих исследовапий им были предложены три группы эмпирических формул.

1. Формулы для определения забойной температуры промывоч­ной жидкости непосредственно после спуска бурильного инструмента (до начала циркуляции) 6,н в °С:

о _ васт + врг ~ 2 ‘

0ijr = e„ + Јclt (VI.27)

(VI. 27а)

2. Формулы для определения минимального значения забойной температуры циркулирующей промывочной жидкости 9а в °С:

0*«.« = е»" + 1с‘’ ‘ "(VI-28)

0,д. и = 0,и, + ^.. (VI.28а)

В = e«°.t+r. e°r. (VI.286)

яа. * Z

3. Формулы для определения величины спада температуры после начала циркуляции 0с11 в °С и времени tca в мин, в течение кото­рого происходит этот спад:

вс„ — 0з„ — е, н. a = L(Cl-сг) = Lc3, (VI.29)

~(03ц ж -0cn) = ctcaЈ = c„L. (VI.30)

13 приведенных формулах приняты следующие обозначения: 0СГ — среднегодовая температура данного района в °С; 06С1 — естест­венная температура пород, пересекаемых скважиной на данной глубине, в СС; 0,их — температура выходящей из скважины про­мывочной жидкости в °С; с, — св — опытные коэффициенты;

L — глубина скважины в м.

Значения опытных коэффициентов с,, с2 и т. д., полученпые Ф. Н. Фоменко для условий скв. 210 площади Лок-Батан, приве­дены ниже.

е»	с,	С,	Сt	г»		°сг’ °с
0,0175	0,0111	0,0064	1,12	0,0125	0,00267	14,5

Учитывая сложность определения опытного коэффициента а в формуле (VI.24), Г. Г. Габузов [131 предложил другой способ нахождения tiH. Рассмотрим схематичный график устьевых и за­бойных температур, представленный на рис. 32.

Здесь линия 1 характеризует распределение естественных тем­ператур пород но глубине, а линия 3 — распределение температуры по стволу скважины в процессе циркуляции промывочной жидкости.

Очевидно, что после прекращения циркуляции в скважине, если ее простои будет достаточно длительным, температура промы­вочной жидкости в конце концов достигнет температуры пород, т. е. линия 3 совместится с линией 1. Тогда можпо допустить, что после прекращения циркуляции, во время подъема и спуска буриль­ной колонны, в скважине установится такое распределение темпера­тур, которое может быть охарактеризовано линией 2, занимающей некоторое средпее положение между линиями 1 и 3. Без большой погрешности можно принять, что такое распределение температур будет одинаковым как для раствора, так и для пород, слагающих стенки скважины. Обозначая указанную температуру через /,,с п полагая тепловой режим скважины установившимся, из рис. 32 найдем, что

t4 ~ rji-f — tji (VI,32)

где а — тангенс угла наклона прямой 2 к оси ординат; h — теку­щая глубина; tv — фиктивная температура, полученная при пере — Ф

сечении прямой 2 с осью температур; Гц — геотермический градиент црп циркуляции, по своей физической сущности соответствующий коэффициенту я в формуле (VI.24); — температура выходящего

Рис. 32. Схема распре­деления температуры ио стволу бурящейся сква­жины.

из скважины раствора.

Так как на участке А В температура рас­твора tn больше температуры tm, а на уча­стке АС меньше нее, то при установившемся температурном режиме промывки указанное условие можно выразить так (201:

/ W (t4 — /ос) dh — / kU (iuc — 1Ч) dh ^ 0,

где II — глубина скважины; U — периметр скважины; к — коэффициент теплопередачи.

Уравнение (VI.33) при независимых и постояппых к и U по глубине можно запи­сать в виде

f(‘4-Qdh~0. (VI. 34)

о

Подставив в (VI.34) значения t и tnc из (VI.32) и (VI.31), после интегрирования по­лучим

а — Г..

(VI.35)

2 (‘Г Дф) И

Из рис. 32 имеем

н ((*11 *>)’

Подставляя это значение Гп в (VI.35) и производя несложные алгебраические преобразования, получим

(VI.36)

Для удобства расчета преобразуем зависимость (VI.36), введя у, — tc

в пес значение а = и значение /. = t. — аII, где

Н — А Уф 3 7 гп з

н / — статические температуры промывочной жидкости, замерен­

ные после подъема инструмента па глубинах II и h (см. рис. 32).

-1-2t4-tr

Подставляя последние значения а и в формулу (VI.36), окон­

чательно получим

ch

21.

это

3Я

Поскольку = яН 1

мулу (VI.37), будем иметь

/

илп

Д

Н —t.

Jf—h то, подставив

Ц

U1

(VI.37) значение в фор-

(VI.37а) (VI.376)

т. е. спад температур на забое скважины Л*, при циркуляции про­мывочной жидкости равен приращению температуры выходящего раствора Д ty.

Соотношение Дt, «=гДty отмечается почти во всех скважинах, где проводились глубинные замеры температуры циркулирующей про­мывочной жидкости (глава IX).

Величины а и t зависят от многих факторов, одиако для одной и той же скважины они зависят в основном от времени простоя скважины без циркуляции т [85]. Чем больше т, тем больше а и тем

меньше tr.

Ф

В нашем случае т определяется временем подъема и спуска бурильного инструмента, поэтому чем глубже скважина, тем больше будет т, а следовательно, и ос.

Но так как тепловой режим стабилизируется в скважине довольно медленно (дни или месяцы), разность времени подъема и спуска инструмента для разных глубин, исчисляемая часами, не должна оказать значительного влияния на величину а.

Для проверки выведенных зависимостей и сделанных предполо­жений по формулам (VI.36), (VI.37) и (VI.37а) была рассчитана вели-

Таблица 26 Площадь № сква­ жины Глу­ бина, м Устьевая темпера­тура 1 , °С С/м V •с *«• °с V °с (действи­ тельное) **Я’ «С (вычи­сленное) Карадаг 291 1070 25,0 _ 15,0 38,0 28,0 28,0 » 291 1508 25,0 — 15,0 46,5 32,0 36,0 » 189 1800 36,0 0,0120 29,0 — 39,0 43,6 » 216 2200 37,0 0,0120 29,0 — 41,0 47,4 » 216 2630 40,0 0,0120 29,0 — 45,5 49,5 » 216 2970 41,0 0,0120 29,0 — 50,0 52,6 » 189 3765 44,0 0,0120 29,0 — 60,0 50,0 Карабаглы 135 2700 31,0 0,0136 15,0 — 34,0 35,7 » 169 3150 24,0 0,0136 15,0 — 39,0 38,8 Озек-Суат 23 2990 62,0 0,0390 — 130,0 87,0 81.0 » 9 3300 10,5 0,0390 — 143,2 142,2 147,2 » 9 3300 21,9 0,0390 — 143,2 141,5 136,0 Тегчай 10 3750 57,0 — 30,0 110,0 83,0 83,0

чина tall и полученные результаты сверены с данными замеров в сква­жинах месторождений Карадаг, Карабаглы, Тегчай и Озек-Суат. Полученные результаты приведены в табл. 26.

Величины а и определены замерами температур в процессе спуска инструмента.

Величину ttH для скважин площади Озек-Суат рассчитывали по формуле (VI.37), причем значение а вычислено по замерам тем­ператур на глубпне 3300 м в скв, 9 п па глубине 2990ж в скв. 23 [76].

30 7600

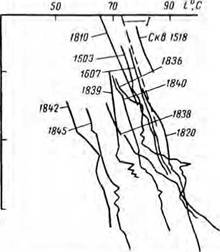
Рис. 33. Термограммы по месторождению Гоусаны, снятые для отбивки цементного кольца.

Как видно из табл. 26, даже ориентировочное опре­деление величин а, *1ф или <, дает вполне удовлетвори­тельный результат для рас­чета ttH по предлагаемому 3000

способу.

Величины а и 1уф, входя­щие в формулу (VI.36), легко определить для каждой сква — j^gg жины, используя замеры мак­симальным термометром в двух-трех точках скважины.

нах а и t

Эти замеры предусматрива­ются в геолого-техническом uooi наряде, составленном для каждой буровой, и входят в комплекс электрометриче­ских работ перед спуском обсадных колонн. После на­копления данных о величи-

вычисленных

Уф*

для ряда скважин, бурящихся на одной и той же площади, можпо сделать вывод о возможности выбора средних величин ад и <„ для всей площади.

* фс

При отсутствии замеров максимальным термометром величины а и можно приблизительно определить, используя электротермо­граммы, снятые для определения высоты подъема цементного рас­твора в аналогичных соседних скважинах.

ные величины t,

V

которые в некоторых случаях равны и даже

Однако анализировать термограмму, снятую для определения ОЦК, следует весьма осторожно. На рис. 33 показаны термограммы по определению ОЦК в 168-жж обсадных колоннах (площадь Гоу­саны). Линией 1 показано распределение естественных температур пород на указанной площади. Как видно из рис. 33, участки термо­граммы, где отсутствует цемент, почти во всех скважинах имеют одинаковый наклон к оси ординат и, следовательно, одинаковые а. Однако если их продолжить, то они отсекут на оси температур раз­
меньше среднегодовой температуры воздуха (скв. 1840, 1842, 1845, 1838); в действительности этого быть не может. Температуры на термограмме скв. 1518 выше, чем пластовые, несмотря на отсутствие цемента в показанном на рисунке интервале.

Указанное несоответствие можно объяснить тем, что методика отбивки ОЦК при помощи электротермометров не преследует цели точных замеров температуры жидкости, находящейся в скважине (термометры поднимаются с разной скоростью, неточно настраива­ются и т. д.). Поэтому, чтобы использовать термограммы ОЦК для

вычислений а и t.. , следует уточнить нх, а также задерживать •Ф

электротермометры в нескольких точках скважины для точного замера температуры находящейся в ней жидкости.

Зависимость, аналогичную (VI.37а), устанавливает и И. А. Кар­манов [28, 29]. Однако он применяет совершенно иную методику решения задачи, и, кроме того, формула И. А. Карманова содержит специальный член, который учитывает потерн тепла на поверхности в процессе циркуляции:

+ (V1-38>

где t3 — температура раствора [па забое по истечении времени т после начала циркуляции; t3o — температура па забое до начала циркуляции; tu — температура раствора у устья в момент восста­новления циркуляции; t7 — то же но истечении времени т; At — охлаждение раствора на поверхности в процессе циркуляции.

Наблюдения И. А. Карманова па промыслах Кубани позволили установить, что летом величина Atu равняется 1—2° С, а зимой —4—5° С; на такие же величины снижается температура раствора на забое скважины.

Г. Г. Поляков [67] провел исследования в бурящихся скважинах объединения Грознефть и на основе исследований предложил эмпи­рическую зависимость для определения забойной температуры в про­цессе промывки:

где — температура на забое скважины перед началом промывки (в °С) по данным температу рных измерений геофизических лабора­торий; L — глубина скважины вл;^ — расход промывочной жидко­сти в л! сек.

В заключение отметим, что хотя эмпирические зависимости проще аналитических, знать последние необходимо. Эти зависимости, построенные в строгом соответствии с общими законами теории теплопередачи, охватывают все параметры, от которых так или иначе зависит процесс теплообмена, и тем самым дают возможность пра­вильно судить о физической сущности происходящих при этом явле­ний. В частности, они позволяют выявить условия для моделирова­ния, что важно при проведении соответствующих экспериментов.

Комментарии запрещены.