Бурение грунтовых зондов, установка энергетических колодцев

Коэффициент температуропроводности глинистых растворов опре­деляли [12] с помощью акалориметра, принцип работы которого основан на первом методе регулярного режима.

Регулярный тепловой режим, теория п практическое осуще­ствление которого предложены в трудах Г. М. Кондратьева и его учеников, является переходным между стационарным и нестацио­нарным режимами.

Период охлаждения или нагрева тела называется регулярным режимом, если распределение температуры внутри тела не зависит от начальных температурных условий, описывается экспонентой и определяется формой, размерами тела и физическим состоянием на его границах.

В стадии регулярного режима

M = tt — tu = Ae-m (11.19)

где tx — температура в исследуемой точке испытуемого материала; ta — температура окружающей среды, предполагаемая постоян­ной; т — время; т — скорость изменения температуры тела, не зависящая от начального состояния системы; А — множитель, зависящий от геометрической формы образца и координат рассма­триваемой точки.

Логарифмируя выражение (11.19), получим

1пД/ = — mt + c, (II.20)

где с — In А.

Из уравнения (11.21) следует, что при регулярном режиме лога­рифм избыточпой температуры линейно изменяется во времени. Поэтому при наступлении регулярного режима температурное поле тела в координатах Ig Д t — т изображается системой параллельных прямых с отрицательным угловым коэффициентом т.

Величина /га, равная тангенсу угла наклона прямой к оси абсцисс, называется темпом охлаждения (нагревания) тела; она пе зависит от расположения системы и времени и может быть определена по формуле

ш 1в(<х—/ц)—Info—tu) (II 21)

Tj-T! ’ ‘

где £, и f2 — температуры тела для двух моментов времени т, и та п стадии регулярного режима.

Как функция критериев Foh Bi и размеров тела она имеет вид (53]:

wx = /(Bi, • • • ) Fo, (И-22)

где Bi = — критерий Бно; Fo = — критерий Фурье; R,

L1( [j2 — размеры тела.

Вид функции определяется формой тела и величиной критерия Bi — Решение уравнения (11.22), когда Bi —юо (или а -> оо), относи­тельно коэффициента температуропроводности а приводит к выра­жению [531

а = ктт, (II.23)

где вю — темп охлаждения (нагрева) тела при коэффициенте тепло­отдачи а —► оо в ч-1; к — коэффициент формы тела в. н*.

Соотношение (11.24) позволяет определить коэффициент темпе­ратуропроводности на приборе, который называется акалориме — тром.

Общая схема примененной аппаратуры показана на рис. И.

Условие а —* оо и t„ — const обеспечивалось с помощью водо­ледяной ванны, в которую опускали акалориметр. Температура водоледяной смеси поддерживалась в течение опыта с точностью 0,08° С и контролировалась с помощью термометра Бекмана. Водо­Ледяная смесь теплоизолировалась пробковой рубашкой.

Коэффициент формы к примененного акалориметра (D — 0,080; Z, = 0,05) определяли по формуле:

*~(2.«И8)» | ^ 3.14 уг = 3373‘10 * (11.24)

Подставляя найденное значение к в выражение (11.24), получим основную расчетную формулу для определения коэффициента температуропроводности. Для данного случая а = 3373 • 10-8 Ша,.

Величину mm определяли из графиков зависимости 1п Д / = / (т). Показания дифференциальной термопары фиксировались через каж­дые 30 сек после погружения образца в водоледяную ванну. Для выяснения возможности определения коэффициента температуро­проводности жидкостей описанным методом собранный акалори-

Таблица Жидкость Темп охла­ждения, тоо. Коэффициент температуро­проводности а*Ю4, м*(ч Относитель­ная ошибка Е, “i замеренный истинный Веретенное масло АУ 8,95 3,01 2,93 2,7 8,90 3,00 2,98 2.4 8,70 2,93 2,93 — Пресная вода 15,00 5,06 4,94 2,4 14,55 4,91 4,94 0,6 14,22 4,81 4,94 2,6

метр был оттарирован с помощью пресной воды и веретенного масла, теплофизические константы которых известны.

Результаты тарировки внесены в табл. 4, из которой следует, что собранный акалориметр может фиксировать коэффициент тем­пературопроводности с относительной погрешностью менее 3%.

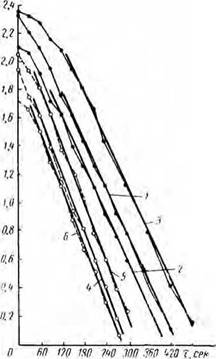
inar Рис. 12. Характерные кривые зависи­мости In — / (т) при определении темпа охлаждения т. 1—з — серии опытов лая глпопетого раствора удельного веса 1,48 Г/см9′, 4—G —то нее, для глинистого раствора удельного веса 1,70 Г/см9.

Определяли коэффициент температуропроводности 11 утяжелен­ных растворов, обработанных 10%-пым раствором УЩР п утяжелен­ных гематитом. Характерные графики зависимости In Д t =

= /(т) показаны на рис. 12.

Параметры глинистых рас­творов и значения коэффици­ентов температуропроводности утяжеленных глинистых рас­творов приведены в табл. 5.

По данным этой таблицы построен график зависимости коэффициента температуропро­водности от удельного веса глинистого раствора (рис. 13).

Из рисунка следует, что коэффициент температуропро­водности липейпо возрастает по мере увеличения удельного веса раствора. Так, при изме­нении удельного веса раствора от 1,45 до 2,00 Г/см[3] коэффи­циент температуропроводности изменяется от 6,6 -10-4 до 9,8-10-“ мг/ч.

Согласно этому рисунку, коэффициент температуропро­водности утяжеленных глини­стых растворов может быть вы­числен по формуле

а = 0,00066

— 0,000581 (у—1,45).

(11.25)

Зависимость (11.25) справед­лива для утяжеленных растворов удельного веса от 1,45 до 2,0 Г хм3.

Как н удельная теплоемкость, коэффициент температуропровод­ности раствора явно зависит лишь от его удельного веса.

В процессе исследований была сделана попытка установить возможную зависимость между коэффициентом температуропровод­ности раствора и степенью его тиксотропии. Для этого глинистый раствор заливали в акалориметр и выдерживали в покое от 1 до 30 мин, после чего замеряли темп его охлаждения.

/500 /600 ПОО 1800 /ЗОО/.Гкм3

15

Рпс. 13, Графики зависимости коэффициента температуропро­водности а, вязкости по СПВ-5 Тъ и водоотдачи В от удель­ного веса утяжеленных глинистых растворов.

Удельный нее, Г/см1	Вязкость по СПВ-5, сек	Водоотдача по ВМ-6, с.«»	Темп охлажде­ния п*оо, ч*‘	Тсмиературопро- водность о-10*. м’/ч
1,48	165	8,3	20,16	6,78
1,48	165	8,3	29,40	6,87
1,48	165	8,3	20,10	6,76
1,49	60	9,0	20,40	6,87
1,49	60	9,0	20,40	6,87
1,49	60	9,0	20,20	6,47
1,54	76	8,0	22,50	7,58
1,54	76	8,0	20,40	6,87
1,54	76	8,0	20,70	6,97
1,55	87	7,0	21,80	7,35
1,55	87	7,0	21,30	7,18
1,55	87	7,0	23,2	7,81
1,68	188	8,0	22,9	7,72
1,68	188	8,0	23,1	7,79
1,68	188	8,0	22,8	7,69
1,70	95	8,0	24,30	8,19
1.70	95	8,0	24,00	8,09
1,70	95	8,0	24,00	8,09
1.77	150	4,5	25,20	8,50
1,77	150	4,5	24,90	8,40
1,77	150	4.5	25,35	8,54
1,80	120	4.0	25,00	8,42
1,80	120	4,0	24,60	8,29
1,80	120	4.0	24,80	8,35
1,84	87	8.0	26,40	8,89
1,84	87	8,0	26,55	8,94
1,84	87	8,0	26,55	8,94
1,90	111	9,0	27,10	9,11
1,90	111	9,0	28,10	9,44
1,90	111	9,0	27,90	9,40
1,95	Не течет	3,5	27,90	9,40
1,95	То же	3,5	27,90	9,40
1,95	»	3,5	27,30	9,20

Таблица

о’.

Несмотря на структурообразование после длительных выдержек глинистого раствора, связи коэффициента температуропроводности со степенью тиксотроппи обнаружить не удалось.

Как было отмечено, теплофизические константы любого веще­ства связаны между собой зависимостью (II. 1), поэтому, располагая экспериментальными данными по определению удельной тепло­емкости с и коэффициента температуропроводности а, можно легко вычислить коэффициент теплопроводности утяжеленных глинистых растворов по формуле (II. 1).

Результаты расчетов по осредненным удельным весам растворов приведены в табл. 6.

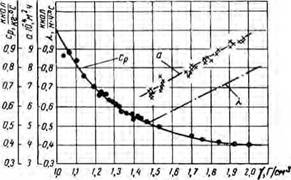
Рпс. 14. Зависимость теплофпзпческпх констант (удельная теплоемкость ср, теплопроводность температуропроводность а) от удельного веса гли­нистых растворов.

Т а б л н цп 1 Удельный пес, Г/см‘ Удельная теплоемкость с, ккал/кг.°С Коэффициент темпера­туропроводности а-10*. м’/ч Коэффициент теплопро­водности А., КОДЛ/м • ч»°С 1,45 0,527 6,60 0,505 1,50 0,516 6,83 0,529 1,55 0,505 7,18 0,562 1,60 0,493 7,47 0,589 1,65 0,482 7,76 0,617 1,70 0,470 8,05 0,643 1,75 0,459 8,34 0,668 1,80 0,447 8,63 0,693 1,85 0,436 8,92 0,720 1,90 0,424 9,21 0,742 1,95 0,413 9,50 0,765 2,00 0,400 9,79 0,784

По зависимостям (11.11), (11.25) и данным табл. 6 построен гра­фик зависимости теплофизических копстапт исследованных глини­стых растворов от их удельных весов (рис. 14).

По этому рисунку коэффициент теплопроводности увеличивается при возрастании удельного веса раствора и может быть определен по следующей линейной зависимости [411:

= 0,51 +0,49 (у-1,45). (11.20)

Комментарии запрещены.