Бурение грунтовых зондов, установка энергетических колодцев

Как было сказано, характер теплообмена во многом зависит от гидравлических свойств теплоносителя, которым при бурении является промывочная жидкость (чаще всего глинистые растворы), а при цементировании цементный раствор.

Как известно, вязкость обычных жидкостей определяется по закону Ньютона

т = (П.27)

где т — тангепциальпое напряжение; ~ — градиент скорости но нормали; ц — коэффициент вязкости.

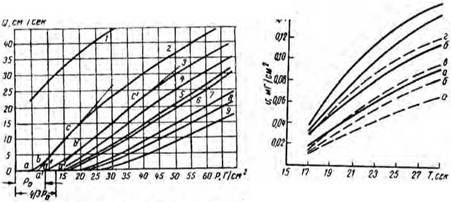
Графически уравнение (11.27) характеризуется прямой ОС (рис. 15) с угловым коэффициентом, равным 1/р, т. е. реологиче­ская кривая истинной жидкости характеризуется одним пара­метром — вязкост

Для реологической характеристики жидкостей, отличных по своим свойствам от ньютоновских, знать один параметр (вязкость) недостаточно.

Так, реологическая кривая, изображающая тело Бингама — Волоровича (кривая 2 на рис. 15), отсекает на оси напряжений некоторый отрезок ОА, поэтому для характеристики этой кривой следует знать уже два параметра — угол наклона прямой и вели­чину отрезка, отсекаемого этой прямой на оси напряжений.

Согласно данным различных авторов в практике исследования глинистых растворов основное место занимают кривые типов 2 и 3, изображенные на рис. 15.

Когда глинистые растворы могут быть охарактеризованы реологиче­скими кривыми типа 2, для нахо­ждения вязкости может быть исполь­зована зависимость, предложенная Бингамом:

T = TiSr^- (IL28>

где т — приложенное касательное напряжение; Т] — коэффициент струк­турной вязкости; 0 — статическое напряжение сдвига.

Величина статического напряже­ния сдвига по своему характеру сходна с пределом упругости и графически изображается отрезком О А или О A j на оси напряжений

(рис. 15, кривые 2 и 3). Численное значение величины Ф может

быть определено выражением

# = (11.29)

которое выводится из условия равновесия пластической жидкости в трубке радиусом R и длиной I (90].

Величина СНС для одного и того же раствора может изменяться при простом механическом перемешивании и зависит от промежутка времени между окончанием перемешивания и началом замера. Поэтому величину Ф замеряют дважды: через 1 и 10 мин после пере­мешивания раствора.

По аналогии с (11.27) выражение (11.28) можпо представить в таком виде:

I du /тт от

В этом случае tj’ называется эффективной вязкостью [90]. Гра­фически она выразится как коэффициент наклона прямой, проведен­ной через начало координат к любой точке (например, к точке Л/, на рис.. 15) реологической кривой АСХ.

В то время как величина т) остается постоянной на всем протя­жении участка АСг, величина т|’ будет меняться для каждой новой точки.

В промысловых условиях для характеристики вязкости поль­зуются показаниями так называемых стандартных полевых вискози­метров (СПВ-5). Эти приборы очень просты и удобны в эксплуата­ции, но по ним можно судить не о структурной или эффективной вязкости, а только об условной вязкости, которая выражается н секундах истечепия испытуемой жидкости через 5-л. н трубку вискозиметра.

В последнее время делаются попытки найти пути использования СПВ-5 для получения данных о структурной вязкости 121], по пока они не получили достаточного подтверждения.

Дело в значительной степени осложняется, если вместо реоло­гической кривой 2 имеется кривая 3. Однако для практики счи­тается возможным рассматривать не всю кривую ЛВС2> а только прямолинейный ее участок ВС2, причем в этом случае уравнепни (11.28) принимает вид:

т = т)^-;-т0 (11.31)

в

П’=Ч + ^. (11.32)

, dn

Величина т0 называется динамическим напряжением сдвига. Под этой величиной имеется в виду отрезок OD па оси напряжений, отсекаемый при продолжении прямолинейного участка ЛС2 кривой АВС до пересечения с осью абсцисс.

В отличие от статического динамическое напряжение сдвига является понятием чисто условным, так как эту величину непосред­ственно замерить на каком-либо приборе невозможно. Она может быть определена лишь в результате экстраполяции прямой части кривой, отражающей зависимость между градиентом скорости и напряжением.

Очевидно, отождествление понятий Ои т0 возможно только в тех случаях, когда эти величины отличаются друг от друга на неболь­шую величину.

В качестве примера на рис. 16 показаны реологические кривые для растворов, приготовленных па пресной воде из глии глино — карьера Карадагского района (кривые получены на приборе типа «Сосуд Мариотта» [40]).

В табл. 9 приведены данные о величинах структурной вязкости и статического напряжения сдвига.

/ 2

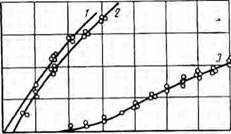
Рис. 17. Глинистый раствор, приготовленный на пресной и морской воде из глин различных карьеров (трубка диаметром 5 мм, длиной 350 мм).

Рис. 16. Глинистый раствор, приготовлен­ный на пресной воле (трубка диаметром 5 мм, длиной 350 мм).

1 — вода; 2—7′ 17 сек. Y = 1,277 Г/см’;

j — Г = 19 сек, V -= 1.307 Г/см’; i — Т =

= 21 сек, у = 1.329 Г/см’; 5 — Т = 22 сек. V = 1.33′. Г/см’; в — Г == 23 сек, Y= 1.333 Г/см*; 7 — Т — 2л сек. V = 1,350 Г/см»; 8 — Т =•

= 27 сек, Y = 1,350 Г/см’; » — Г — 29 сек,

Y — 1.363 Г/см».

I — ни пресной воде, 2 — на морской воде; карьеры: а — Карадагскнй,

6 —• Кировский в — Орджоник вазов­ский, а — Ленинский.

Таблица 9 Гллнокарьеры С и о Карадатского района Кировского района Ленинского района Карачухурского района л t- •• о 3 «3 ч и «• 3 (J К к .с* .ь« л- а & а> Л> Ч «еГ< «> -5

На пресной воде 17 0,0380 18,2 0,0272 28,9 0,0295 40,0 0,0273 33,9 19 0,0507 32,6 0,0378 44,3 0,0326 62,1 0,0851 52,5 31 0,052-4 45,0 0,0383 61,7 0,0379 89,3 0,0406 75,0 23 0,0560 59,3 0,0424 77,1 0,0433 116,8 0,0417 98,9 25 0,0679 70,0 0,0469 95,0 0,0423 131,1 0,0418 118,2 27 0,0704 82,5 0,0532 104,6 0,0428 145,7 0,0466 127,5 29 0,0816 92,9 — — 0,0448 153,2 0,0469 143,6

На морской воде 17 0,0444 11,8 0,0558 11,8 0,0484 26,7 0,0446 11,8 19 0,0546 24,3 0,0638 26,4 0,0488 50,0 0,0533 31,4 21 0,0637 32,1 0,0828 39,3 0,0483 68,2 0,0658 46,4 23 0,0801 39,3 0,0851 52,1 0,0532 86,0 0,0744 63,6 25 0,0972 48,6 0,1026 62,5 0,0495 98,9 0,0706 75,0 27 0,1079 59,3 0,0986 72,5 0,0504 111,4 0,0854 85,4 29 0,1173 67,5 0,1009 81,1 0,0564 120,0 0,0893 95,7

На рис. 17 показано изменение статического напряжения сдвига в зависимости от относительной вязкости глинистых растворов.

В табл. 10 приведены параметры, характеризующие свойства

утяжеленных глинистых растворов, Q. си Усек ’60 40 ВО’ »0 0 40 ВО 120 ’60 200 240 0, си Рис. 18. Зависимость расхода цементного раствора от напора. г—— = 0,50 (035): г—— = 0,45; а — — = с с с = 0,30 (0.28).

полученных постепенным утяжелением исходного раствора, приготовленного из глин Кировского рай­она г. Баку. Растворы приготовляли на пресной и морской воде и обраба­тывали УЩР; утяжели­телем в первом случае был концентрат Калашни­ковой пыли (исходный рас­твор № 1), а во втором — барит (исходный раствор № 2). Реологические свой­ства определяли на ротаци­онном вискозиметре Фила­това — Жуховпцкого.

Как видно из рассмо­тренных примеров, реоло­гические параметры утяжеленных глинистых растворов, характеризу­ющие его физико-механические свойства, увеличиваются с повышением

Таблица III Количество утяжелителя по весу, % Вязкость по СПВ-5, сек Удель­ 3, мГ/см‘ -| пробы ный вес, Г/см> за 1 мин за 10 мин т„ па OUfl t C. il* Исходный _ 40 1,26 81,5 114 0,27 69 раствор. V* 1 1 50 40 1,56 105 182 0,28 60,5 2 100 42 1,79 158 276 0,35 62 3 150 44 1,97 185 333 0,38 80 4 200 54 2,12 244 394 0,40 90 5 250 76 2,25 400 — 0,46 115 Исходный 40 1,20 110 136 0,27 72,5 раствор № 2 1 50 75 1,52 250 272 0,32 110 2 100 03 1,79 153 294 0,48 151,5 3 125 177 1,88 153 236 0,54 190 4 150 240 1,99 177 260 0,73 252 5 200 Не течет 2,02 141 472 0,73 321 С 250 То же 2,14 425 685 1,07 428

удельного веса раствора. Темп этого увеличения в зависимости от типа и количества применяемого реагента н дисперсности твердых частиц в растворе может быт различным. На рис. 18 показаны кривые зависимости расхода цементного раствора от напора, полученные онытпым путем. Из этих кривых хорошо видно, что характер изме — пения расхода цемептпого раствора в зависимости от напора меняется

w

с изменением его водо-цементного отношения —.

Аналогичные кривые были получены и М. А. Абдиновым [40].

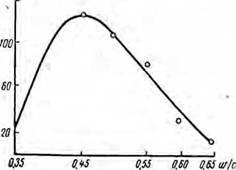
Изменение статического напряжения сдвига цементного раствора в зависимости от водо-цементного отношения показано на рис. 19.

t/.мГ/см 7 Рпс. 19. Изменение статического напря­жения сдвига цементного раствора в за­висимости от водо-цементного фактора.

В заключение отметим, что структурно-механические свойства глинистых растворов могут значительно изменяться под воздей­ствием температуры. В Со­ветском Союзе первые иссле­дования в этом направлении были выполнены в АзНИИДН под руководством проф.

Р. И. Шищенко. Исследова­ния проводились на специ­ально сконструированных для этого приборах, которые позволяли определять водоот­дачу, структурную вязкость и статическое напряжение сдвига при температуре выше 100° С [91, 92].

В дальнейшем исследо­ванию влияния температуры на структурно-механические свойства глинистых раство­ров уделялось больше внимания, и в настоящее время в этом направлении известны многие работы, наиболее полный обзор которых выполнен Г. Я. Дедусенко и Е. А. Яишниковои [241.

Температура довольно существенно влияет на вязкость. При этом можно считать установленным, что в общем случае структур­ная вязкость глинистых растворов, приготовленных любым способом, так же как и вязкость чистой воды, с увеличением температуры уменьшается. При этом вязкость раствора в сравнении с вязкостью воды может изменяться по-разному: снижаться несколько быстрее или медленнее [33, 47, 56, 91, 96 и др.], не изменяться, иметь мак­симум или минимум [16, 91].

Данных о влиянии температуры на изменение эффективной вяз­кости нет.

Зависимость вязкости от давления (от 1 до 200 кГ/см2) проявляется сравнительно слабо. Но в общем с увеличением давления вязкость жидкостей возрастает.

Обобщая имеющиеся в литературе сведения [1, 47, 91, 96|, можно заключить, что статическое напряжение сдвига любых гли­нистых растворов с увеличением температуры непрерывно растет, причем в некоторых случаях может наблюдаться максимум, после которого величина О снова уменьшается. Точка максимума для различных растворов различпа.

Некоторые авторы считают, что динамическое напряжение сдвига т0 не изменяется с увеличением температуры или незначи­тельно уменьшается [33], имеет сложную зависимость с максимумом п минимумом [16].

Статическая н динамическая водоотдача обычных глинистых растворов с ростом температуры увеличивается, а водоотдача рас­творов, обработанных щелочной вытяжкой из бурого угля, остается почти без изменения [1, 2 и др.].

Комментарии запрещены.