Бурение грунтовых зондов, установка энергетических колодцев

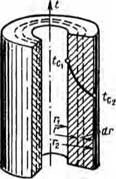
Рис. 3. Распределе­ние температуры в од­нородной цилиндри­ческой стенке.

Из сказанного выше вытекает, что для решения задач, связан­ных с теплообменом в бурящихся скважинах, в первую очередь должны быть выяснены качественная и коли­чественная характеристики явления передачи тепла через стенки бурильных и обсадных труб, участвующих в исследуемом процессе.

Поэтому прежде всего рассмотрим теплопро­водность однородной цилиндрической стенки.

Для этого примем, что колонна труб (бу­рильная или обсадная) имеет по всей длине I одинаковые наружный и внутренний dz диаметры и выполнена из материала, коэф­фициент теплопроводности которого равен Я и постоянен для всех ее точек. Далее примем, что внутренние источники тепла в колонне от­сутствуют, температура изменяется только в радиальном направлении и поддерживается постоянной и равной /с, на внутренней по­верхности трубы и tCt — на ее наружной по­верхности; при этом <г, <с, (рис. 3).

Выделим внутри стенки колонны кольцевой слой с впутренпим радиусом г и толщиной dr. Тогда внутренняя поверхность этого слоя по всей длине колонны будет

F ^2лг1,

а температурный градиент

g rad* = — g-.

Подставляя найденные величины в уравнение (1.1а) Фурье, найдем, что количество тепла, проходящее в единицу времени через выделенный слой, будет равно

Q ——k/’gradf — —Я2л т1~. (1.3)

Разделив в уравнении (1.1а) переменные и проинтегрировав его, найдем

t~— 2ni r~tc’ (1.5а)

где с — постоянная интегрирования, которая находится из гранич­ных условий, согласно которым t = tCl при r = rt, t — tCl при г = г>. Поэтому

С ~ + Т, . 1п Г а.

°г 1 2пМ г Подставив найденное значение с в (1.5а), получим

/ = _М1пг’,'<с!+’21г1пГг i

или, подставив вместо t и г соответствующие им значения tr, и rlt найдем, что

2лХ/

откуда

(16)

In —

Т

Из полученного уравнения следует, что количество тепла, пере­данное через однородную стенку цилиндрической трубы в течение 1 ч, прямо пропорционально коэффициенту теплопроводности Я, длине Z, температурному напору (<Ct — tc,) и обратно пропорцио­нально натуральному логарифму отношения наружного радиуса г2 к внутреннему г,.

Уравнение (1.6) остается справедливым и для случая, если тепло­вой поток будет направлен в обратном направлении, т. е. при усло­вии, если iCl < ta,.

Поэтому для более общего случая целесообразнее записать

Q = — At (ккал/ч). (1.6а)

“1

Из этого уравнения следует, что внутри однородной цилиндриче­ской стенки температура изменяется по логарифмической кривой (рис. 3).

Величина Q может быть отнесена либо к единице длины, либо к единице поверхности, в результате чего будут получены различные размерности.

Так, если Q отнести к единице длины трубы /, то расчетная фор­мула примет вид:

-j — = <7, =>At (ккал/м * ч); (1.7)

In — г —

‘h

если же Q будет отнесена к единице поверхности, то

(ккал/м2 — ч).

(1.8)

Q _ Q 2). At

F ndA Чг. , гl2

d‘ln ITT

Так как здесь могут быть приняты и внутренняя (F = Flt d. = dj) и внешняя (F = F2, d(. = d2) поверхности, то значения удельных тепловых потоков qFи qF будут различны. Связь между q,, qF и qF может быть определена из соотношения

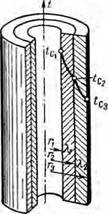
‘/V q, = nd1qFt = ndiqFt (ккал/м-ч). В практике бурения может встретиться и более сложный случай передачи тепла через цилиндрическую стенку, когда последняя со­стоит из нескольких слоев. Например, передача тепла через техническую колонну, которая после цементирования покрывается кольцом це­ментного камня определенной толщины (рис. 4). При стационарном тепловом режиме через все слои будет проходить одно и то же коли­чество тепла. Следовательно, в соответствии с выражением (1.6) для каждого слоя можно составить следующее равенство:

(1.9)

Рис. 4. Распределе­ние температуры в многослойной цилчв- дрпческой степке.

„ _ *0j) q‘~ ~Г^~’ т-а~ м “1 2я (*.,-*„) ‘ dt Из этих уравнений можно каждого слоя

(1.10)

(1.10а)

найти изменение температуры для

~JLl in ! 2л Хг *

(Ml) (1.11a)

-L

do

— t =——— In. »* S 2л X» [1] do •

t

Очевидно, что, суммируя перепады температур для каждого слоя, т. е. складывая отдельно все левые и все правые части системы уравнений, аналогичных (1.11) и (1.11а), можно получить полный температурный напор между внешней и внутренней поверхностями многослойной стенки. Так, для примера, изображенного на рис. 4, при таком суммировании получим

/с —t — —■ {In ~ — f In ^2- ) . ci сз 2л )Л </t ‘ Хе dt /

Зная полный температурный напор, нетрудно определить вели­чину теплового потока q

п — Чч) ЧI * j f j

(1.13)

Если представить изменение температуры в многослойной ци­линдрической стенке графически, то получим ломаную кривую. В то же время внутри каждого слоя температура будет изменяться так же, как и при однородной стенке, т. е. по логарифмическому закону (рис. 4).

Аналитическое выражение для температуры на поверхностях соприкосновения слоев можно получить, подставляя значение q, из (1.13) в (1.11) и решая последнее относительно того или иного значения t„.

Если толщина стенки трубы мала по сравнению с диаметром (т. е. отношение d2/d1 <,2), то влиянием кривизны стенок обычно пренебрегают и теплопроводность трубы рассчитывают по форму­лам для плоской стенки. Формула для определения значения удель­ного потока, проходящего через многослойную плоскую стенку, имеет следующий вид:

Л1 ’ ‘ ‘ Я;

(1.14)

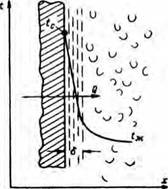
незначителен и можно считать, что весь теплообмен внутри потока обусловливается его теплопроводностью. При турбулентном же ре­жиме, отличающемся хаотическим движением потока, возника­ющие в нем вихри создают благоприятные условия для проникно­вения отдельных масс от ядра потока к стенкам, перенося некоторое количество тепла. Но так как теплопроводность жидкостей сравни­тельно невелика, основной причиной теплообмена является интен­сивность переноса количества движения. Однако и в первом и во втором случаях у самой стенки образуется так называемый погра­ничный подслой толщиной б (рис. 5), который, будучи неподвижным, может проводить тепло исключительно в результате теплопровод­ности.

Рис. 5. Расвределение темпе­ратуры при движении вязкой жидкости вдоль плоской стенки.

Таким образом, поскольку в про­цессе передачи тепла соприкосновением движущейся жидкости со стенкой ос­новную роль играет конвекция, то пе­редачу тепла в этом случае называют конвективным теплообменом пли тепло­отдачей.

При решении задач, связанных с конвективным теплообменом, основной является формула, вытекающая из за­кона теплообмена Ньютона:

Q — aF(t0 — t’t)^-aF t (ккал/ч) (1.15)

или в дифференциальной форме

dQ = aAtdF, (1.15а)

где F — площадь теплообмена в м2;

At = t0 — tx — разность температур (температурный напор) между стенкой и соприкасающейся

с ней жидкостью в °С; а — коэффициент теплоотдачи или конвекции в ккал/м2-ч-°С.

Коэффициент теплоотдачи показывает, какое количество тепла в килокалориях передается от соприкасающейся среды к поверх­ности стенки площадью 1 мг в течение 1 ч при условии, что разность температур между средой и стенкой составляет 1° С.

Теплоотдача относится к категории сложных процессов, проте­кание которых зависит от многих факторов. Так, кроме перепада температур между средой и стенкой Д t, на теплоотдачу существен­ное влияние оказывают форма стенки Ф, ее геометрические размеры /], /г, состояние поверхности (шероховатость) е. Но менее важное влияние на характер теплоотдачи оказывают физико-механические и теплофизические свойства движущейся среды (теплоносителя), такие, как коэффициент теплопроводности X, удельная теплоемкость ср, плотность р, кинематическая v или динамическая р. вязкость, коэффициент температуропроводности а и др.

Теплоотдача зависит также и от природы возникновения и ско­рости v движения теплоносителя, а также от того, движется ли жидкость внутри канала (трубы) или омывает его.

Комментарии запрещены.