Бурение грунтовых зондов, установка энергетических колодцев

Удельная теплоемкость 1 глинистых и цементных растворов определялась методом дифференциального электрокалорнметра (37, 381, который основан на определении степени нагрева двух жидкостей, палптых в одинаковые калориметры, под действием одного и того же электрического тока, равного по своей величине некоторому числу / .

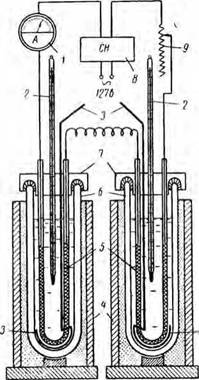
На рис. 8 показана схема этой аппаратуры. В качестве калори­метрических сосудов применялись сосуды Дюара емкостью по 0,5 л. Электронагреватели изготовлялись из стандартной никельхромовой проволоки с таким расчетом, чтобы сопротивление спиралей было одинаковым п равным 50 ом.

Для измерения температуры применялись лабораторные ртутные термометры с ценой деления шкалы 0,1° С. Термометры подбирались совершенно одинаковыми по форме, весу и интервалам шкалы (от 0 до 50° С). В процессе опыта раствор все время перемешивался специальными мешалками.

Перед началом исследований в оба калориметра заливали оди­наковое количество (но 450 мл) жидкости, причем в один калориметр заливали испытуемую жидкость, а в другой — жидкость, теплоем­кость которой заранее была известна. Затем замыкали цепь питания электронагревателей и отсчитывали температуры по термометрам при непрерывном перемешивании жидкостей.

Так как оба электронагревателя включались в цепь последова­тельно, то в каждом из калориметров выделялось одинаковое коли­чество тепла.

-3

Рис. 8. Экспериментальный диффе­ренциальный алектрокалориметр.

=■=£[<

с2т2 + w2,

1 — амперметр; г — термометры; 3 — мешалки; * — кожух; s — электрона­греватели; в — сосуды Дюара; 1 — крыш­ки; в — стабилизатор напряжения; » — реостат.

Обозначая через Q количество тепла, которое выделялось в тече- ние некоторого времени работы электронагревателей, можно напи- сать + )(t2—tl), <? = (сгтг+и>г)(*;-0, где с, и с, — удельные теплоемко- сти первой и второй жидкостей; тп1 н т2 — массы жидкостей; и w2 — водяные эквиваленты внутренних сосудов первого и второго калориметров с мешалками и термометрами; ty и t2 — на- чальная и конечная температуры первой жидкости; t и f’ — те же величины для второй жидкости. Приравняв правые части вы- ражений (II.3) п определив из полученного уравнения одну из теплоемкостей (папример, Cj), найдем (П.4) Так как во второй сосуд Дюара в течение всех замеров заливали дистиллированную воду, то вели- чину с2 можно принять равной 1 ккал/кг-°С, а поскольку оба калориметра были приготовлены из двух совершенно одинаковых сосудов, то водяпые числа калори- метров Wy и w2 можно принять равными, т. е. wx —w, — w. Тогда выражение (II.4) примет вид:

ш3 (t2 tj) w /, n… r 1 mi (<i—h) P. h—’ * . Определение величин t2, t[, t2 является паиболее трудной и важной задачей, так как от этих величин в значительной степени зависят результаты всей работы. Поэтому повышать температуру в калориметрических сосудах нужно со скоростью, достаточной для того, чтобы термометры восприняли температуру жидкости с точностью, соответствующей их тепловой инерции. Для обеспече-

ния такой скорости повышения температур найдена соответству­ющая сила тока I, которая поддерживалась в течение всех замеров постоянной в результате включения в схему (см. рис. 8) стабилиза­тора напряжения, амперметра и ползункового реостата.

Величины tlf <г, t[ и определяли известным способом.

Наибольшие трудности встретились при определении водяных чисел дюароных сосудов, поэтому величиной w препебрегли; оконча­тельная расчетная формула приобрела вид:

„ _ »«аса(^2 — <!) /II о

тх(1,-/0 ■ <11Ь)

Нетрудно показать, что такое пренебрежение величиной в нашем случае вполне допустимо. В тарировочпой табл. 1 приведены результаты замеров удельных теплоемкостей жидкостей, теплофизи­ческие константы которых были заранее известны 179].

Т а б л п п а 4 Жидкость, залитая в калори­ Вес залитой жидкости, 3 Удельная тепло­емкость жидкости, залитой в калори­метр i, ккал/ти “С Абсолют­ная по­ метр 1 калори­метр 1 калори­метр 2 замерен­ ная (средняя) ио извест­ным данным с. грешность С —С з я Дистиллированная вода. . . Глицерин (динамитный) . . . Глицерин (дистиллированный) Веретенное масло АУ. . . 500 WM,5 525,07 384,45 500 494,98 445,67 447,17 1,01 0,578 0,576 0,476 1,00 0,578 0,58 0,47 ±0,017 -0,002 -0,004 f0,006

Примечание. В калориметр 2 залита только дистиллированная вода.

Из приведенной таблицы следует, что вычисленная после заме­ров по формуле (II.6) удельная теплоемкость отличается от своего истинного значепия не более, чем на величину абсолютной ошибки, равной ±0,01 ккал/кг С, что говорит о возможности сделанного допущения: w = wx = w2 = 0, поэтому все последующие расчеты были проведены по формуле (II.6).

После того как калориметры были оттарированы, приступили к определению теплоемкости глинистых растворов. Исследуемые глинистые растворы приготовляли на морской воде из карачухур — ской глины и определяли их основпые параметры: удельный вес, вязкость по СПВ-5, статическую водоотдачу (на приборе ВМ-6) и статическое напряжение сдвига на 1 и 10 мин (прибором СНС-2).

Удельпая теплоемкость глинистых растворов

Исследовали удельную теплоемкость нормальных, химически обработанных и утяжеленных растворов, которые наиболее часто применяются при бурении скважин в Азербайджане.

			Среднее
Вязкость пи СПВ-5,	Водо­	Статическое	значение
отда­	напряжение	удельной
ча,	сдвига аа 1 и	теплоем­
	е. н»	10 лик, аГ/м’	кости, ккал/ка • °С

Удельный нес, Л/ел»

Нормальные растворы. 1,07 16 40 — 0,880 Лабораторный 1,15 18 36,5 — 0,760 » 1,24 19 32 80/100 0,685 » 1,26 27 31,5 100/120 0,670 » 1,33 46 30 180/200 0,605 » 1,37 Не течет 23 Более 200 0,570 » 1,40 То же 20 * 200 0,565 » 1,415 » 19 » 200 0,560 $ 1,426 » 16,5 » 200 0,555 » 1,44 » 14 —/200 0,550 » 1.30 23 40 Химич ески обработаны 0,630 ые растворы Из скв. 157 (забой 3130 м) 1,043 16 — — 0,870 10%-пый раствор УЩР 1,10 — — — 0,840 Лабораторный 1,15 18 32 -/4,54 0,750 » 1,20 20 27,5 48,06/59,07 0,710 » 1,23 22 24 49,9/65,1 0,670 » 1,28 30 19 73,78/130,2 0,640 » 1,31 52 14,5 108,5/136,7 0,620 » 1,34 60 13 Более 200 0,580 л 1,37 150 — » 200 0,570 » 1,42 Ир течет 1 » 200 Г тяжеленные pat 0,550 •творы » 1,465 50 21 147,56/158,4 0,525 Лабораторный 1,57 47 20 102/115 0,520 » 1,70 150 17 Более 200 0,450 » 1,85 200 13 » 200 0,425 » 1,90 55 10 91/158 0,418 » 2,00 Не течет 9 Более 200 0,400 » 1,54 135 6 * 200 0,490 Ия ска. 183 (забои 4267 л) 1,76 180 7 » 200 0,480 Из скв. 164 (забой 2600 м) 2,00 120 4 » 200 0,48 Из скв. 199 (забоя 2686 м)

Раствор

Таблица 2

Для исключения влияния находящихся в глине примесей каждую новую порцию раствора изготовляли из глины, взятой в разных местах карьера.

Раствор обрабатывали 10%-ным раствором УЩР с удельной теплоемкостью 0,87 ккал/кг-°С и утяжеляли его гематитом.

Кроме растворов, приготовленных в лаборатории, исследовали также растворы, взятые из бурящихся скважин площади Карадаг.

Удельную теплоемкость для каждого раствора определяли от 6 до 8 раз. Всего было исследовано 30 растворов, имеющих различ­ные параметры; при этом было проведено около 230 замеров, осред — ненные результаты которых приведены в табл. 2.

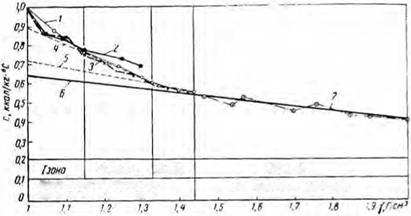
В первой серии опытов исследовано 10 образцов нормальпых глинистых растворов удельных весов от 1,07 до 1,44 Г/см3. Изме­нение параметров глинистых растворов и средних величин удельных теплоемкостей показано графически на рис. 9.

Из рисунка видно, что величина удельной теплоемкости пормаль — ных растворов с увеличением удельного веса (плотности) умень­шается и находится в пределах от 0,88 до 0,55 ккал/кг-‘С.

Изона

Шзона

П зона

Утяжеленные растворы

Нормальные и линически обработанные растворы

Рис. 9. Зависимость удельной теплоемкости глинистых растворов от удельного веса.

1 — нормальные растворы; 3 — нормальные растворы по данным Н. И. Шапова;

М — химически обработанные растворы; 4—е — касательные к кривым с — / (у);

7 — утяжеленные растворы.

Зависимость с = /х (у) изображается кривой, касательная к ко­торой увеличивает наклон к оси ординат с увеличением удельного веса раствора.

Так как величина удельного веса зависит от концентрации глины в воде, то удельная теплоемкость обратно пропорциональна коли­честву глины в растворе, которая вследствие своей удельной тепло­емкости (около 0,22 ккал/кг — ° С) занижает удельную теплоемкость воды, являющейся второй составной частью нормальных рас­творов.

Во второй серии опытов исследовали химически обработанные растворы, которые приготовляли из нормального раствора удель­ного веса 0,42 Г/см3 с удельной теплоемкостью 0,55 ккал/кг-0С обработкой его 10%-ным раствором УЩР с удельной теплоемкостью 0,87 ккал/кг-°С и добавлением некоторого количества морской воды. В результате исследования девяти образцов растворов,

приготовленных таким образом, было найдепо, что величина удельной теплоемкости при изменении удельного веса от 1,42 до 1,10 Г/см3 колеблется в пределах от 0,84 до 0,55 ккал/кг • °С.

Как видно из рнс. 9, зависимость с = /2 (у) для химически обра­ботанных растворов (кривая 3) так же, как и для нормальных рас­творов, изображается кривой, показывающей обратно пропорцио­нальную зависимость величины удельной теплоемкости от удель­ного веса раствора.

Так как химически обработанные растворы были составлены из трех компонентов — воды, глины и 10%-ного раствора УЩР, то величина удельной теплоемкости этих растворов несколько умень­шилась по сравнению с нормальным раствором такого же удельного веса. Кривая зависимости с = /а (у) для химически обработанных растворов расположена несколько ниже или полностью совпадает с аналогичной кривой для нормальных растворов (см. рис. 9).

В третьей серии опытов определяли удельную теплоемкость утяжеленных растворов и растворов, которые брали на буровых.

Утяжеленные растворы готовили на базе нормального раствора удельного веса 1,42 Г/см3 с удельной теплоемкостью 0,55 ккал/кгС добавлением гематита и 10%-ного раствора УЩР. Исследовано шесть растворов удельного веса от 1,46 до 2,0 Г/см3.

Величины удельной теплоемкости в исследованном интервале удельных весов снижаются от 0,525 до 0,40 ккал/кгС. Результаты исследований изображены на рис. 9, из которого видно, что зависи­мость с = /3 (у) для утяжеленных растворов можно принять линей­ной и обратно пропорциональной (кривая 7).

Результаты исследований утяжеленных растворов, взятых из скв. 99, 157, 183, 164 площади Карадаг, помещены в табл. 2. Иссле­дованиями выявлено, что зависимость с = / (у) для растворов, взятых нз скважин и приготовленных в лабораторных условиях, полностью совпадает, несмотря на различие их других параме­тров.

Угол наклона касательной к оси ординат при увеличении удель­ного веса растворов постепенно увеличивается и приобретает по­стоянное значение при удельных весах, соответствующих утяжелен­ным растворам (линии 4—6).

С достаточной для практики точностью кривую зависимости с — f (у) можно разбить на четыре прямолинейных участка (см. рис. 9), для каждого из них зависимость с — / (у) можно при­нять линейной и определить по следующим формулам:

(11.7)

а) при бурении водой с примесью удельного веса от 1 до 1,15 Г/см3 (I зона)

с = 1 — 1,6 (у—1);

(И.8)

б) при бурепии нормальным и химически обработанным рас- творо. м удельного веса от 1,15 до 1,33 Г/см3 (II зона)

с = 0,76 — 1,21 (у —1,15);

211
при бурении теми же растворами удельного веса 1,33—1,44 Г/см3 (III зона)

с = 0,60-0,636 (у-1,33); (11.9)

в) при бурении утяжеленным, химически обработанным раство­ром удельного веса от 1,44 до 2,0 Г/см3 (IV зона)

с = 0,53-0,23 (у-1,44). (11.10)

Найдена также общая зависимость для всех четырех зон при расчетах удельной теплоемкости, дающая абсолютную погрешность порядка ±0,01 ккал/кг-°С:

с = 0,334 -]-0,6745у_::’3. (11.11)

Формулы справедливы как для растворов, приготовленных в лабораторных условиях, так и для растворов, взятых со скважин.

В заключение отметим следующее.

Авторы работы [51] на основании своих исследований приходят к выводу о том, что «теплоемкость глинистых растворов различных типов подчиняется правилу аддитивности и может быть рассчитана по теплоемкости отдельных компонентов пропорционально их содер­жанию, в связи с чем экспериментальное определение этой величины излишне».

Однако если первая часть вывода не вызывает никаких сомнений, то со второй частью согласиться нельзя.

Используемый в промысловой практике глинистый раствор представляет собой многокомпонентную систему, которая частичпо образуется в стволе скважины в процессе разбуриванпя пород. Поэтому гораздо проще экспериментально определить непосред­ственно теплоемкость раствора, чем сначала выполнить (также экспериментальным путем!) сложные работы по определению содер­жания компонентов, их теплоемкости и удельного веса, а потом только паходить теплоемкость раствора по закону аддитивности. Использование же справочных данных об удельном весе и тепло­емкости входящих в глинистый раствор компонентов может при­вести к серьезным погрешностям.

Так, авторы работы [51], критикуя экспериментальные данные по удельной теплоемкости глинистых растворов [38], исходили из предположения, что удельный вес применявшейся и опытах глины составлял 2,60 Г/см3. Но последний был равен 2,05 Г/см3 и таким образом фактическое максимальное отклонение наших данных от данных, полученных более точным способом, составляет всего 3,4%, а не 13,1%, как это утверждается в работе [51]. С учетом же теплоемкости связанной воды ошибка снижается до 2%.

Удельная теплоемкость цементных растворов

Теплоемкость цементного раствора сц р определяли [35] на элсктродифференциальном калориметре, описанном рапее. Опыты проводились с цементными растворами, имеющими подо-цемсптные

отношения Г-7 J от 0,40 до 1,00 и взятыми с интервалом 0,05. Удель­ный вес этих растворов (приготовленных из цемента Карадагского завода на пресной воде) изменялся в пределах 1,48—1,92 Г/см3. Средняя продолжитель-

Рис. 10. Зависимость удельной теплоемкости цементных растворов от удельного веса и от водо-цсмевтиого отношения. = 20-ь46° С) в зависимости от удельного веса и водо­цементного отношения. Как видно из рис. 10, средняя величина сц р с изменением удель­ного веса раствора у в рассматриваемом интервале изменяется по

’.6 0.2

сз

Таблица 3 Цементный раствор Количество жидкости в сосудах калориметра, г Удельная теплоемкость цементного раствора е ккал/кг-°С водо-цементное отношение w/c удельный вес 1, 1’/см‘ цементный раствор, Рл. р вода, Р по опыту (средняя) по формулам (11.15), (И. 17) 0,400 1,92 883,63 453,32 0,371 0,421 0,400 1,92 833,08 452,91 0,367 0,421 0,425 1,88 757,32 465,90 0,384 0,431 0,450 1,85 843,40 465,42 0,390 0,441 0,475 1,81 845,85 462,77 0,420 0,450 0,500 1,78 812,48 465,55 0,420 0,460 0,550 1,73 813,23 465,19 0,424 0,477 0,000 1,69 739,80 449,10 0,472 0,493 0,650 1,66 788,60 459,78 0,466 0,509 0,700 1,63 759,70 452,42 0,474 0,523 0,750 1,60 684,20 526,27 0,515 0,537 0,800 1,57 741,63 451,55 0,520 0,548 0,850 1,54 713,45 459,60 0,528 0,568 0,900 1,52 706,50 456,40 0,535 0,575 0,950 1,50 706,92 467,61 0,538 0,584 1,000 28 1,48 694,50 462,00 0,566 0,595 ность времени с момента затворения цемента до окончания опытов каждой серпы с определенным во — до-цемснтным отношением не превышала 25—30мин. Величины с„ опреде­ляли из зависимости, аналогичной (II-6). В табл. 3 приведены средние значения с„ р по всем замерам для каждого образца цементного рас­твора. На рис. 10 пока­заны изменения средней величины с„ р (при t =

0.6

ЦЧ

1.4 о

18 0.8

‘.9 ГО

о. ч

0.6

наклонной под определенным углом прямой. В интервале значений у = 1,48 1,92 Г/с. ч3 уравнение прямой, характеризующей ся.

цементного раствора, имеет вид:

сл. Р = 0,56-0,42(у-1,45). (11.12)

Зависимость си. изображается кривой 2, причем

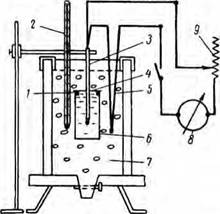
Рис. 11. Схема экспериментальной ус­тановки для определения коэффициен­та температуропроводности глинистых растворов.

с увеличением темп возрастания сд р, снижаясь, стремится к по­стоянству. Это объясняется тем, что при больших значениях

— мы практически будем иметь

воду, теплоемкость которой в процессе опыта постоянна.

Продолжение левой части кри­вой 2 пересекается с осью ор — ш п

динат в точке, где — = U, а

си р = 0,19, что соответствует удельной теплоемкости сухого цемента с. к.

Если принять, что сп р =

= ф f "7 ) в рассматриваемом

интервале изменяется по прямой 2 (рис. 10), то уравнение (11.12) примет вид:

1 — уплотнение; 2 — термометр Бекиапа; 3— керамическая трубка: 4 — крышка акало- рнметра; 5 — дифференциальная термопара; в — акалориметр; 7 — водоледяпая смесь; в — гальванометр; 9 — потенциометр.

с„. р = 0,38 + 0,325 ^ “— 0,4 ) .

(11.13)

Полученные опытные данные сопоставлялись со значениями теплоемкости цементных растворов, найденной по формуле

С — CjXj — f — СрХр — f — • •., (11.14)

где с,, с2— удельные теплоемкости веществ, из которых состоит смесь; агх, хг — относительные количества веществ, из которых состоит смесь (здесь. .=100%).

Для нахождения удельной теплоемкости цементного раствора, состоящего из сухого цемента Рс. ц и воды P’„t формулу (11.14) запишем в виде

4* се. п^о. к tfsP« 4" P<s. Чсс. И /Т1

си. р — —р^гъ—————————— = р •————— (11.15)

*»T*Oe ц *ц. р

где cCt ц — удельная теплоемкость сухого цемента, равная 0,19 ккалЫг — °С; с„ — удельная теплоемкость воды, равная 1,0 ккал/кг-°С; Ри — вес цементного раствора.

Если вес воды Pt, находящейся в цементном растворе, обозна­чить через w, а вес сухого цемента Р0 и через с, то Рп „ = w л-с, следовательно,

„ Ш_р

… wPu в с ^ ..

= (НЛО)

* W—C 1

с

Зная Рц р и — (табл. 3), по формуле (11.16) определяем коли­чество воды, находящейся в испытываемом растворе. Результаты расчетов приведены в этой же таблице.

Подставляя значение Р’„ из уравнения (II. 16) в зависимость (11.15), получим

и>

с “Ч-есв.„ …

сч. ц— . tv ~ W + C * (

1 J —————-

с

Если имеем песчано-цементную смесь, то па основе уравнения (11.17) для этого случая можно написать

ш4-сс. „4-с„р„

С0 = ц. р= V’V, (П.18)

где са — удельная теплоемкость песка; ра — вес песка.

Таким образом, теоретическая величина удельной теплоемкости цементного раствора может быть подсчитана как по формуле (11.15), так и по формуле (11.17). В первом случае должны быть известны количества воды Р’в и сухого цемента Ре ц, находящиеся в цемент­ном растворе, и удельная теплоемкость сухого цемента сс ц, а во

втором — достаточно знать водо-цементное отношение — и теплоем­кость сухого цемента е0 ц.

Удельные теплоемкости с, подсчитанные по формулам (11.15) и (11.17), даны в табл. 3.

Значения сц р, найденные по этим формулам, превышают опыт­ные величины для данного цементного раствора лишь па 0,04 ккал/кг • °С.

Таким образом, величину удельной теплоемкости цементного и песчано-цементпого растворов можно определить как по опытным данным, так и по теоретическим зависимостям.

Комментарии запрещены.