Бурение грунтовых зондов, установка энергетических колодцев

В бурящейся скважине процесс теплопередачи сложнее, так как здесь имеется не одна колонна, а две или более, расположенные концентрично или эксцентрично.

2 Заказ 1080, 17

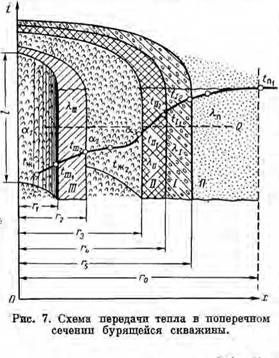
Рассмотрим концентричное расположение труб (рис. 7).

Примем, что тепловой поток движется в направлении от по­роды П к промывочной жидкости Ж„ находящейся внутри буриль­ных труб III.

При этом тепловой поток последовательно проходит через цемент­ное кольцо I, трубы промежуточной колоппы II, восходящий поток промывочной жидкости Ж2 и бурильные трубы III. Согласно обо­значениям, принятым на рис. 7, для установившегося теплового состояния системы, когда количество тепла, отданное горячей и

0 ‘гя^и[1Лш~{ги) 1 — Ч‘~ In d4ld3 :

принятое холодной жид­костью, будет одним и тем же, можно составить следующие равенства:

а) для потока тепла, идущего от породы к внеш­ней стенке трубы /,

Q „ 2 л ^п(1пь~1и)

т.„.— I.

d&

б) для потока тепла, идущего от внешней стенки трубы / к внутренней ее стенке,

2В).,

I 41 Indb/di »

в) для потока тепла, идущего от внутренней стенки трубы I (или от внешней стенки трубы II) к внутренней стенке тру­бы II,

г) для потока тепла, идущего от внутренней стенки трубы II к восходящему потоку жидкости Ж2,

у — = = <*and3 (*п, — <ж5);

д) для потока тепла, идущего от жидкости Ж2 к наружной стенке трубы III,

Т"7′ — (‘W, — *ш„);

е) для потока тепла, идущего от наружной степки трубы III к внутренней ее стенке,

I ~4t— lndj/rfj »

ж) для потока тепла, идущего от внутренней стенки трубы III к жидкости Ж j,

f = ql = a1Kd1 (tuu-t ж,).

Составленные равенства позволяют определить частные темпе­ратурные перепады, складывая которые, можно найти полный температурный напор в рассматриваемой системе:

+ 2X^1d *7 + ‘5а] = 1Г Г'( ^’22)

где г, — полное термическое сопротивление.

Отсюда в соответствии с (1.21) определим искомую величину к, для рассматриваемого случая:

1

1 , do I i rfs I I d I 1 I ^ I

it. n lD db + 2Л7 + Xn lD d3 + a3d3 + ajd-i

1 • 1 ln^-( (1.23)

ai^i 2Яjtx

А выражение для потока тепла примет вид:

^ —<h — k, n{t п, ^Kj)* (1‘24)

Глава II

ТЕПЛОФИЗИЧЕСКИЕ СВОЙСТВА

ПРОМЫВОЧНЫХ ЖИДКОСТЕЙ И ГОРНЫХ ПОРОД.

РЕОЛОГИЧЕСКИЕ СВОЙСТВА ГЛИНИСТЫХ РАСТВОРОВ

Теплофизические константы любого вещества связаны между собой следующим соотношением:

А = аср, (II. 1)

где А — коэффициент теплопроводности п ккал/м • ч • °С; а — коэф­фициент температуропроводности в м2/ч с — удельная теплоем­кость в ккал/кгС; р — плотность в кг/м3.

Полагая у известным, можно считать, что для получения всех трех теплофизических констант достаточно найти какие-нибудь две из них.

Удельная теплоемкость (с) вещества представляет собой то количество тепла, которое необходимо для нагревания 1 кг вещества на 1° С. Если теплоемкость определяется при постоян­ном давлении, то ее обозначают через с (ккал/кгС), а если при постоянном объеме, то через су (ккал/кгС). Из определения имеем

с ~ п^дГ (ккал/’ * с)*

где ДQ — количество тепла; т — количество вещества в кг; Д< — приращение температуры в °С.

Коэффициент температуропроводности характеризует собой скорость изменения температуры единицы объема среды, т. е. изменение ее температуры за единицу времени. Из (П-1) имеем

а = ^(м*/ч). (Ц.2)

Если можно считать, что теплофнзические свойства ньютонов­ских жидкостей и газов изучены довольно полно (Н. Б. Варгафтик, Н. В. Цедерберг 179] и др.), то этого нельзя сказать о таких жидкостях, как глинистые и цементные растворы.

В этом направлении известны лишь исследования Н. И. Шацова [871 по определению удельпой теплоемкости нормальных растворов из 11 различных глин. Анализ результатов этих исследований показал, что теплоемкость нормальных растворов с увеличенном удельного веса снижается.

Об изменении удельной теплоемкости химически обработанных и утяжелешшх растворов, теплопроводности и температуропровод­ности глинистых н цементных растворов в литературе сведении нет. Исключение составляют некоторые косвенные сведения об ориенти­ровочном значении коэффициента теплопроводности глинистого рас­твора. Так, некоторые авторы в тепловых расчетах принимают коэффициент теплопроводности нормального глилистого раствора равным 0,5 ккал/м-ч0С.

В работе В. Л. Шсвелькова приводятся данные о коэффициенте теплопроводпости глины в зависимости от ее вдагосодержания. Согласно этим данным глина при 50%-пом влагосодержапии имеет коэффициент теплопроводности 1,25 ккал/м • ч • °С. При меньшем и большем влагосодержапии этот коэффициент снижается до 0,5 ккал/м-ч-°С. По данным того же автора коэффициент темпера — туропроводпости глины возрастает от 0,5-10"[2] до 5-10-4 мг/ч при увеличении ее вдагосодержания от 5 до 55%.

Комментарии запрещены.