Бурение грунтовых зондов, установка энергетических колодцев

Обычно коэффициент диффузии дисперсного тела определяют из выражения

Di = 82О0,

где 62 — пористость дисперсного тела; Do — молекулярный коэффициент диффузии данного раствора соли.

В работе [Шехтер Р., 1971 г.] получено выражение, которое ограничи­вает коэффициент диффузии электрически нейтрального тела сверху:

, £)2<8г£)о[1—(1 —в2)/3].

Таким образом, коэффициент диффузии находят из приближенных теоретических выражений, которые справедливы для дисперсных тел

65

5 Заказ 1935
с электрически нейтральной поверхностью. Но на коэффициент диффузии существенное влияние оказывает электрическое взаимодействие с поверх­ностью твердой фазы. Согласно теоретическим положениям физической химии на коэффициент диффузии влияет концентрация электролита. Обычно с ростом концентрации электролита электрокинетический потен­циал падает и система переходит в изоэлектрическое состояние. Па­раллельно этому происходит снижение коэффициента диффузии до минимального значения. В последнее время также обнаружено, что электрокинетический потенциал существует и в дисперсиях с высоким со­держанием электролита, т. е. зависимость потенциала от концентрации имеет немонотонный характер.

Ниже представлены результаты экспериментального определения коэффициента диффузии в широком диапазоне концентраций. Суть ис­пользованного метода заключается в следующем. Испытуемый матери­ал — кварцевый песок или водный раствор портландцемента (среда 1) по­мещается в нижнюю часть вертикально расположенного цилиндрического сосуда. Поровое пространство заполняется жидкостью с равномерной начальной концентрацией ионов. Над испытуемым материалом размеща­ется эталонная среда 2 — жидкость с более низкой концентрацией ио­нов. В момент соприкосновения сред 1 и 2 начинается процесс диффузии, т. е. в контактирующих системах формируются нестационарные поля кон­центрации. Среды 1 и 2 считаем полуограниченными, поэтому продол­жительность эксперимента выбираем такой, чтобы диффундирующие ионы не достигали нижней и верхней границ испытуемой и эталонной сред.

Расположим начало координат на границе контактирующих сред, а ис­ходную концентрацию ионов в среде 2 примем за начало отсчета. При ма­тематическом описании процесса считаем, что для каждой из двух сред справедливо обычное диффузионное уравнение

dCi д*с,

TOC o "1-5" h z ~дГ~ Dl~dT~’ (41)

где С/, Di, t их — концентрация, коэффициент диффузии, время и коорди­ната; i — среда.

Краевые условия имеют вид

х = 0, />0 DxdCiJdx = DtfCi/dx, С, = С2; (4.2)

х<0, t = О С| = Со и х>0, t = О С2 == 0, (4.3)

где Со — избыточная начальная концентрация ионов в поровом объеме дисперсного тела.

Используя результаты работы [69], решение задачи (4.1) — (4.3) для среды 2 записываем в форме

. C2(x, t) = C0D{ 1 —erf[x/(2 /5J)]}, (4.4)

где D= fD/(VD+ /D2); erf [x/(2/Dlt)] — интеграл вероятности.

Элементарную массу ионов, поступивших в среду 2, найдем из выра­жения

дС2 I ‘ dm = Di-j^-Sdt I х=о, (4.5)

где 5 — площадь контакта сред 1 и 2.

Подставляя выражение (4.4) в (4.5) и интегрируя в пределах от О до /, с использованием правила дифференцирования определенного интег­рала по параметру получаем

TOC o "1-5" h z т = 4SC0D2Dt/ /4nD2t. (4.6)

С другой стороны, правую часть выражения (4.6) можно представить в виде.

т = ACSR(t). (4.7)

Здесь АС — изменение концентрации данного иона в эталонной среде за время массообмена.

В равенстве (4.7) неизвестной величиной является R(t) — глубина проникновения ионов в среду 2. Для ее определения представим выраже­ние (4.4) в приближенной форме [7], которая хорошо аппроксимирует истинное поле концентрации:

С2(х,0 = C0D(-x/Rf, (4.8)

где R — приближенное значение глубины проникновения ионов в среду 2.

Учитывая, что для полуограниченного тела при />0, CoD = const, и используя вариационный метод, получаем

R — l/U,3 D2t. (4.9)

Приближенное значение утечки массы в среду 2 получим из выражений (4.5), (4.8) и (4.9) в виде

т = 4SC0D2Dt/ уП 1,3D2t. (4.10)

Сопоставляя выражения (4.6) и (4.10), точное значение R записываем в виде

R= V4nD2t. (4.11)

Полагая Dz — Do (роль эталонной среды выполняла дистиллирован­ная вода), из равенств (4.6) и (4.7) получаем выражение для коэффициен­та диффузии ионов дисперсного тела

£>, = kDo, (4.12)

где А = £ji-^-/(l—J2; Do — молекулярный коэффициент диффу­зии ионов.

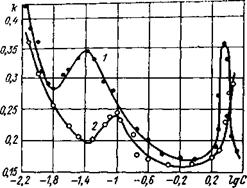
Рис. 4.1. Зависимость коэффициента k (кварц фракции 0,1—0,16 мм) от концентрации водного раствора. I — КС1, 2— СаС12.

Эксперименты проводили с кварцевым песком, который кипятили в кон­центрированной азотной кислоте, а затем отмывали до нейтральной реак­ции в дистиллированной воде и высушивали при 105°С. Затем навески кварцевого песка засыпали слоем 2 см в стеклянные стаканы цилиндри­ческой формы, которые помещали в эксикатор и в течение 1 ч вакууми- ровали с разрежением 0,5 • 104 Па. Далее, не снимая вакуума, поровое пространство заполняли водным раствором CaCU или КС1. Подготовлен­ная таким образом испытуемая среда проходила термостатирование при 25°С до установления равновесного состояния. Затем отбирались излишки раствора вровень с поверхностью испытуемой среды. После этого сверху осторожно доливалась дистиллированная вода с той же температурой 25°С, т. е. процесс диффузии начинался и протекал в течение 72 мин при постоянной температуре. Продолжительность опыта 72 мин выбрана из тех соображений, чтобы объем воды был достаточен для определения концентрации ионов.

По истечении 72 мин эталонную среду осторожно отбирали пипеткой вровень с поверхностью кварцевого песка (захват раствора из порового пространства среды 1 исключался) и определяли ДС. Толщину слоя эта­лонной среды 2, отбираемой для анализа, находим из формулы (4.11). Молекулярный коэффициент диффузии ионов водного раствора КС1 и СаСЬ принимаем по данным работы [49]. Концентрацию ионов С1_ опре­деляли титратором Т-201, ионов К+ — методом пламенной фотометрии, а ионов Са2+ — объемным титрованием. Оценочные эксперименты показа­ли, что при определении концентрации по ионам К+ или С1~, а также Са2+ или С1_ различий не наблюдается. Поэтому в дальнейшем все определе­ния проводили по иону С1- с 5—б-кратной повторяемостью.

Экспериментальные данные на рис. 4.1 и 4.2 показывают, что зависи­мость коэффициента k от концентрации электролита имеет своеобразный

характер. Для объяснения закономерности изменения представим k в виде

‘ »

* = (*i+fe2)e,, (4.13)

где k и ^2 — коэффициенты, учитывающие извилистость порового про­странства и электрические свойства дисперсного тела; ei — объемная по­ристость.

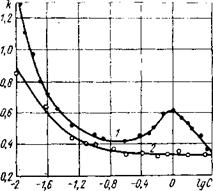
Рис. 4.2. Зависимость коэффициента k (кварц фракции 1—2 мм) от концентрации водного раствора. /-КС!; 2 — СаС1г.

Однозначной характеристикой электрических свойств дисперсной фа­зы является основной параметр двойного электрического слоя (ДЭС) — электрокинетический потенциал, который при рН=2 окружающего кварц раствора становится равным нулю, т. е. система переходит в изоэлектри — ческое состояние (ИЗС) [Чураев Н. В., 1984 г.]. В этом случае ki = О и равенство (4.13) принимает форму

k = kle>. (4.14)

Определение k в ИЗС было выполнено при заполнении порового про­странства кварца водным раствором НС1 концентрации 0,1 М с pH=2. По­лученные значения k равны 0,32 и 0,17 соответственно для крупно — и мелкозернистого кварца при е* = 0,4. Если бы поровые каналы имели прямолинейную форму и не сообщались между собой, то ki = 1 и согласно формуле (4.14) k = 0,4. В действительности ft<0,4, т. е. /ei<l. Используя полученные в ИЗС значения k, составляющие 0,32 и 0,17, имеем k соот­ветственно 0,8 и 0,43, т. е. извилистость (длина пути диффундирующих ионов) порового пространства мелкого песка выше, чем крупного. Откло­нение величины k от k& — const определяет влияние электрического взаимодействия ионов с дисперсной фазой.

На рис. 4.1 и 4.2 показано, что при умеренных концентрациях электро­лита в заполняющей поровое пространство жидкости отмечается тенден­ция к снижению k с ростом С. Отрицательный потенциал поверхности кварца, создаваемый ионами ОН-, компенсируется избыточным потенциа­лом ионов К+ или Са2+, находящихся в диффузной части двойного элект­рического слоя. Это приводит к уменьшению ki в формуле (4.13), а значит, и k. Полученный результат соответствует данным работы [Чураев Н. В., 1984 г.], где резкий спад потенциала поверхности кварца фракции 100— 250 мкм отмечается при С>0,01 М^т. е. в области исследованных нами концентраций.

Кварц (рис. 4.3) имел следующий фракционный состав, %: более 1 мм — 0,02; от 1 до 0,63 — 1,92; от 0,63 до 0,4 — 18,63; от 0,4 до 0,315 — 25,4; от 0,315 до 0,25 — 25,78; от 0,25 до 0,2—15,86; от 0,2 до 0,16 — 5,94;

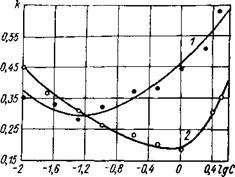
Рис. 4.3. Зависимость коэффициента k поли- фракционных тел от кон­центрации водного раство­ра КС1. / — портландцемент; 2 — кварц.

от 0,16 до 0,1—3,81; менее 0,1 — 0,06. Фракционный состав портландце­мента определить не представляется возможным, так как в контакте с водой происходит диспергирование цементных частиц. Однако очевид­но, что он также является полифракционным. Характер поведения кривых отличается от данных на рис. 4.1 и 4.2 наличием одной экстремальной точки. Закономерность изменения k портландцемента соответствует опы­там с кварцем, однако экстремальная точка смещена в область более низких концентраций. Такое отличие можно объяснить тем, что заряд по­верхности гидратированного портландцемента имеет скорее всего положи­тельный знак [8]. Подавление электрокинетического потенциала, видимо, происходит под влиянием ионов С1_, которые специфически адсорбируют­ся на частицах цемента [8], т. е. компенсация потенциала поверхности происходит быстрее. Более высокое минимальное k объясняется порис­тостью 0,53 против 0,4 у кварцевого песка. Минимальное значение k квар­ца соответствует данным рис. 4.1.

В целом результаты рис. 4.1—4.3 имеют сложный немонотонный харак­тер. В настоящее время нет общепринятой трактовки электрокинетических явлений в концентрированных растворах электролитов. Рядом авторов по­казана вероятность увеличения потенциала частиц, что объясняется раз­личной растворяющей способностью сольватного слоя относительно ка­тионов и анионов. Другим объяснением, которое также рассматривалось в литературе при анализе экспериментальных данных, могут быть поло­жения теории сильных электролитов [76]. Согласно этой теории в кон­центрированных растворах формируются ближний порядок распределе­ния ионов и осциллирующий потенциал вокруг иона. Высказано предпо­ложение, что в концентрированных растворах и вокруг заряженной час­тицы потенциал будет осциллировать, т. е. зависимость k от концентра­ции электролита будет иметь немонотонный характер. Интересно отме­тить, что экстремальные точки на рис. 4.1 в случае заполнения порового объема кварцевого песка раствором СаСЬ смещены в область более вы­соких концентраций. Возможно поэтому отсутствует экстремум на ниж­ней кривой рис. 4.2.

В зависимости от концентрации и состава порового раствора коэффи­циент диффузии может изменяться в широких пределах. Так, на рис. 4.2 h сначала изменяется от 1,3 до 0,4, т. е. коэффициент диффузии умень­шается в 3,25 раза. В дальнейшем k возрастает в 1,5 раза и вновь падает до значения около 0,32, что соответствует полученному в изоэлектриче — ском состоянии. В целом k изменяется от 1,3 до 0,32, т. е. снижается в 4,3 раза. При заполнении порового пространства кварцевого песка раст­вором хлористого кальция k монотонно стремится к тому же значению 0,32.

Для мелкозернистого кварца получено два максимума. При этом пов­торное возрастание k более значительно, чем в случае крупнозернистого кварца: в 2 раза. Коэффициент диффузии в диапазоне исследованных концентраций уменьшается в 2,5 раза.

Таким образом, минимальное значение коэффициента диффузии лими­тируется только извилистостью порового пространства дисперсного тела. При малых концентрациях электролита диффузию в основном определяет коэффициент /гг, т. е. силы электрического взаимодействия ионов с поверх­ностью твердой фазы. В области высоких концентраций коэффициенты k и ki имеют один порядок.

Комментарии запрещены.