Бурение грунтовых зондов, установка энергетических колодцев

При течении промывочных жидкостей или цементных растворов в трубном и кольцевом пространстве скважины формируется распреде­ление скоростей — профиль скорости. Поскольку буровые жидкости яв­ляются неньютоновскими системами, то их реологические свойства могут в существенной степени зависеть от скорости сдвига. Это следует, напри­мер, из экспериментальных результатов на рис. 1.4—1.6. Таким образом, представляет практический интерес определить скорости сдвига жидкос­тей в трубном и кольцевом пространстве. Имея экспериментальную зави­симость т — t и значения ^ в скважине, можно найти реальные реологи­ческие свойства циркулирующей жидкости.

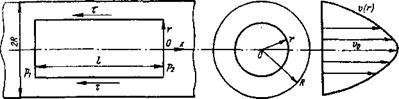
С целью простоты изложения найдем профиль скорости в установив­шемся ламинарном потоке ньютоновской жидкости в прямой круглой тру­бе диаметром D = 2R. Используем закон трения Ньютона (1.3). Согласно условию прилипания скорость течения жидкости на стенке равна нулю, а в средней части имеет наибольшее значение. Характерной особенностью ламинарного течения является то, что отдельные концентричные слои скользят один по другому, причем скорость каждого слоя имеет только осевое направление. Поскольку в потоке имеет место трение, то движение жидкости в трубе происходит под действием перепада давления р>р2 (рис. 1.7). При этом в каждом поперечном сечении, перпендикулярном к оси трубы, давление является постоянным, т. е. зависит только от про­дольной координаты х.

Составим условие равновесия цилиндра жидкости длиной I радиусом г и с осью, совпадающей с осью трубы (см. рис. 1.7). В направлении оси х на цилиндр действуют силы давления pinr2 и р^пг1, приложенные к лево­му и правому основаниям. По боковой поверхности цилиндра действует касательная сила 2лл/т. Следовательно, условие равновесия имеет вид

SHAPE * MERGEFORMAT

(1-6)

Отсюда

nr2(p —pi) — 2nrlx.

t = (Pi—Рг)г/(2/).

Рис. 1.7. Ламинарное течение ньютоновской жидкости в круглой трубе.

Скорость v уменьшается с увеличением г, поэтому закон (1.3) запишем со знаком минус

т = —iAv/dr. (1.7)

Приравняв выражения (1.6) и (1.7), получим dv/dr = —(pi—р2)г/(2р0-

После интегрирования

v(r) = (p,-p1XC-r2/4)/(ц0-

Постоянную интегрирования С найдем из условия прилипания жидкос­ти к стенкам трубы, т. е. v = 0 при г = R. Отсюда С = R2/4 и

о(г) = (р,-р2Х/?г-гг)/(4цО — (1-8)

Наибольшее значение скорость имеет в середине трубы при г — 0, где она равна

оо = (р,-/>2)Я7(4р/)-

Расход жидкости через поперечное сечение трубы Q найдем из условия, что объем параболоида вращения у(г) (см. рис. 1.7) равен половине про­изведения площади основания на его высоту:

<2 = я/?7о/2=я/?Ч/>.-Р2)/(8цО — (1.9)

Выражение (1.9) называют законом Хатена — Пуазейля ламинарного течения в трубе. Расход жидкости через поперечное сечение трубы можно представить с использованием средней скорости течения: Q = лR2v. Тогда, вместо выражения (1.8) получим

t/(r) = 20[1—(г//?)2] = 80{г/(2/?>—[г/(2/?)]2). (1.10)

Получить зависимость, аналогичную (1,10), для кольцевого простран­ства скважины принципиальных затруднений не представляет. Однако учитывая громоздкость и неудобство выражения, целесообразно кольце-

9

вую трубу заменить плоской, ширина которой h = (D—d)/2. Применяя использованный выше подход, получим, профиль скорости в плоской трубе

v(r)=6v[r/h-(r/hn (1.11)

Известно, что на гидравлические сопротивления, режим течения или интенсивность теплообмена основное влияние оказывает тонкий слой жид­кости вблизи стенки трубы. Поэтому в практических расчетах нужно знать градиент скорости сдвига на стенке трубы, по которому находим фак­тическую вязкость промывочной жидкости в скважине. Дифференцируя выражение (1.10) и подставляя г — R, с учетом D = 2R, получаем ско­рость сдвига на стенке круглой трубы

dv/dr = t = 85/D. (112)

Дифференцируя равенство (1.11), подставляя г — Он h=(D—d)/2, получаем скорость сдвига на стенке плоской или кольцевой трубы

dv/dr = ? = 12V/{D-d). (1.13)

Если выполнить аналогичные преобразования с использованием вмес­то равенства (1.3) выражения (1.5), то получим скорость сдвига на стенке применительно к степенной модели Рейнера — Оствальда: для круглой трубы

dv/dr = у — 80&/D, 0-14)

где б = (Зп+1)/(4л);

для плоской или кольцевой трубы

dv/dr = у=12v6/(D-d), (1.15)

где б = (2л+1)/(Зя).

При п = 1 (ньютоновская жидкость) выражения (1.14) и (1.15) пере­ходят в равенства (1.12) и (1.13).

Для вязкопластичной жидкости, которой соответствует выражение (1.4), скорость сдвига на стенке можно представить в следующем виде: для круглой трубы

dv/dr = ‘(’ = 806/D; (1.16)

для плоской или кольцевой трубы

dv/dr = у = 2vb/(D—d). (1-17)

Здесь

то

= 0,81/[l-b2(l+Vl-fSn)/Sn]. (1.19)

Тс

Выражение (1.19) получено в работе [59]. Параметр Сен-Венана в ра­венстве (1.19) для круглой и кольцевой труб представлен следующими выражениями: Sn = xqD/{t^) и Sn = To(D—d)/(ilT).

Полученные в данном разделе выражения скоростей сдвига можно использовать, например, для расчета эффективной ньютоновской вязкости неньютоновских жидкостей или оценки возможности использования в практических условиях той или иной реологической модели путем со­поставления скоростей сдвига в скважине и на реометре.

Комментарии запрещены.