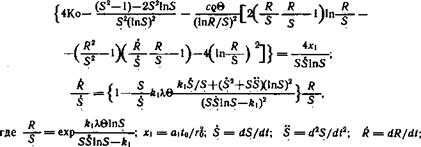СОПОСТАВЛЕНИЕ ТЕОРЕТИЧЕСКИХ ЗАВИСИМОСТЕЙ С ДАННЫМИ ФИЗИЧЕСКОГО, ГИДРАВЛИЧЕСКОГО И ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
СОПОСТАВЛЕНИЕ ТЕОРЕТИЧЕСКИХ ЗАВИСИМОСТЕЙ С ДАННЫМИ ФИЗИЧЕСКОГО, ГИДРАВЛИЧЕСКОГО И ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
Физическая модель. Проверка зависимости (2.27) при небольших значениях критерия Коссовича Ко, т. е. при наиболее жестких условиях, выполнена на лабораторной установке [62]. Высота и диаметр модели составляли 0,6 м. Торцевые поверхности теплоизолировались пенополиуретаном толщиной 50 мм. Через центр пласта проходила медная трубка с внутренним и наружным диаметрами 14 и 16 мм. Вода с постоянными температурой (49°С) и расходом циркулировала снизу вверх, пока фронт протаивания не достигал термопары № 7. В течение этого времени последовательно фиксировалось прохождение нулевой изотермы через термопары № 3—7, установленные в средней по высоте части модели. Прохождение нулевой изотермы через термопары № 1 и 2 достоверно зафиксировать не удалось в связи с небольшим периодом времени и нестационарностью процесса теплообмена в первые моменты от начала циркуляции. Термопара № 3 была установлена на расстоянии 36 мм от наружной поверхности медной трубки, а последующие на равном расстоянии друг от друга 15 мм. Во время опыта контролировалась температура на термопаре вблизи боковой поверхности, а также на двух термопарах, расположенных ближе к торцам модели. Особенностей в их показаниях не зафиксировано.
Кварцевый песок перед началом опытов имел температуру —1,5°С, для которой характерно практически полное замерзание воды (см. рис. 2.1). Утечками тепла за границу раздела фаз пренебрегаем в связи со значительным отличием температуры песка и циркулирующей жидкости. Пренебрегаем также перепадом температур на стенке медной трубки в связи с малой толщиной и высокой теплопроводностью. Массовая влажность песка W = 0,11, а экспериментально определенные теплофизические свойства в талом состоянии имели следующие значения: Xi ==
= 1,95 Вт/(м*°С); Ci = 1090 Дж/(кг*°С); qi = 1820 кг/м[1]; ai = = 9,8-10~7 м2/с. Эти показатели удовлетворительно соответствуют табл. 2.1.
|
33 |
Данные табл. 2.4 показывают хорошую сходимость результатов расчета с экспериментом, что подтверждает Справедливость предлагаемой методики расчета радиуса плавления при небольшом значении критерия Ко = 0,69.
Сопоставление эксперимента с расчетом радиуса плавления
|
29,1 |
63,1 |
125 |
215 |
309 |
|
6,4 |
8,8 |
10,7 |
13,4 |
15,5 |
|
6,0 |
8,5 |
11 |
13,5 |
16 |
|
+6,7 |
+3,2 |
-2,8 |
—0,75 |
-3,2 |
|
Число Фурье Foi |
|
Расчет по формуле (2.27) Эксперимент Расхождение, % |
|
Способ определения радиуса плавления |
Гидравлическая модель. Для проверки формулы (2.27) при относительно высоких значениях критерия Ко были использованы классические результаты [Новиков Ф. Я., 1959 г.], полученные на гидроинтеграторе. Поскольку гидравлическая модель представляет собой систему (2.6)— (2.8), то полученные на интеграторе результаты эквивалентны точному решению.
При расчете радиуса плавления по формуле (2.27) воспользуемся методом последовательных приближений. Сначала допустим, что So изменяется во времени так, как он изменялся бы в соответствии с зависимостью
(2.27) , но при фо = 1. Определенное из такой предпосылки значение So будет, очевидно, завышено против истинного. Подставляя завышенное So в выражения (2.11) и (2.18), получаем заниженное фо, а из формулы
(2.27) — заниженное So — Подставляя это значение So в выражения (2.11) и (2.18), получаем завышенные фо и So. Истинное положение цилиндрической поверхности протаивания заключено между завышенным и заниженным значениями. Если полученная в первом приближении «вилка» окажется слишком широкой, то переходим ко второму приближению. Для чего повторяют вычисления, воспользовавшись предыдущим значением So, до получения удовлетворительных результатов.
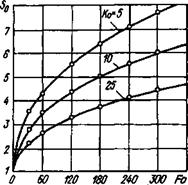
Рассмотрим пример расчета для самого неблагоприятного случая из представленных на рис. 2.2: Ко = 5 и Fo = 300. Полагая фо = 1, из зависимости (2.27) получаем So = 11,8. Первое приближение — So = 11,8. Из выражений (2.11) и (2.18) фо = 0,683, vo = 0,614. Тогда фо = 9§vo =
|
|
|
Рис. 2.2. Сопоставление расчетов (кривые) по формуле (2.27) с данными гидромоделирования (точки). |
= 0.6832 * 0,614 = 0,283 и S0 = 6,83. Из выражений (2.11) и (2.18) фо = = 0J75, vo = 0,666. Тогда фо = 0.7752- 0,666 = 0,4 и So = 7,88. Отклонение от среднего значения So составляет 7,1%/Во многих случаях такой точности достаточно. При необходимости переходим ко второму приближению. Повторяя расчеты, получаем «вилку»: 7,62 и 7,68. Отклонение от среднего значения 0,39%. В большинстве практических случаев можно ограничиться вторым приближением, причем для процесса бурения достаточно первого приближения. Несмотря на необходимость выполнения повторных операций, процесс расчета является простым и непродолжительным, так как зависимости (2.11), (2.18) и (2.27) просты по структуре.
Данные сопоставительного расчета представлены на рис. 2.2, откуда следует полное совпадение теоретического выражения (2.27) с результатами гидромоделирования.
Численная модель. Основной целью численного моделирования является проверка справедливости зависимости (2.29), которая учитывает утечки тепла в мерзлую зону через границу протаивания. Если для решения задачи (2.6) — (2.8) воспользоваться интегральным методом, то принимая температурное поле в талой и мерзлой зонах квазистационарным, получаем систему дифференциальных уравнений
|
|
|
ср = C2Q2/C1Q1; t = 7/fo; в = Г„/Г0; R = Lt/r0 = 1+ |/4F02; F02 = att/rl X = = Х2/Х1, k = XTato/(wqrb). |
|
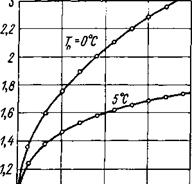
Рис. 2.3. Сопоставление расчетов (кривые) по формуле (2.29) с численным решением (точки). |
|
(2.30) |
|
(2.31) |
|
|
|
S |
0 4 8 12 F0
|
3* |
35
Результаты расчета на ЭВМ ЕС-1022 (рис. 2.3) показывают полное совпадение теоретических формул (2.27) и (2.29) с численным решением. Исходные данные были приняты следующими: Xi = i,86 Вт/ (м • °С); с — = 1100 Дж/(кг-°С); ei = 1900 кг/м3; К2 = 2,32 Вт/(м-°С); с2 = = 880Дж/(кг-°С); q2 = 1900кг/м3; ег№ = 250кг/м3; q=335* 103 Дж/кг; То = 4°С, 7п = —5°С и го = 0,2 м.