Бурение грунтовых зондов, установка энергетических колодцев

Одной из наиболее сложных и ответственных технологических опе­раций при строительстве скважин различного назначения является креп­ление растворами вяжущих материалов, из которых с течением времени формируется искусственный камень определенной прочности. Прочность камня, который выполняет целый ряд функций, зависит от глубины пре­вращения исходного вяжущего в продукты реакции. В общем случае пре­вращение вяжущего протекает в неизотермических условиях, что связано с экзотермическим характером химических реакций.

Большая заслуга в изучении экзотермии цементов принадлежит С. А. Миронову, В. В. Кинду, С. Д. Окорокову, И. Д. Запорожцу и другим исследователям. Установлено, что наиболее важными факторами, влияю­щими на экзотермию, являются химический и минералогический состав цемента, крупность его помола, температура окружающей среды и началь­ная температура раствора, тип и количество химических добавок и напол­нителей. Влияние некоторых из перечисленных факторов применительно к тампонажным цементам рассмотрено в предыдущих разделах.

Из четырех основных минералов портландцемента наибольшей экзо — термичностью отличается трехкальциевый алюминат, а наименьшей — двухкальциевый силикат. Трехкальциевый силикат и четырехкальциевый алюмоферрит занимают промежуточное положение. Предельные значения экзотермии перечисленных минералов после полностью завершенного процесса гидратации обычно принимают следующими, кДж/кг: СзА 1050; C3S 670; C4AF 590; p-C2S 340.

Причиной выделения тепла при твердении цемента является экзотер­мическая реакция гидратации, причем суммарный эффект складывается из теплоты смачивания порошкообразного цемента водой, растворения цементных минералов в воде (обычно сопровождается поглощением тепла), химических реакций присоединения воды с образованием гидрат — ных фаз, кристаллизации и других фазовых переходов в твердеющем це­ментном камне и теплоты адсорбции воды на продуктах реакции. По вкла­ду в экзотермию перечисленные факторы являются неравноценными: наиболее значительное влияние оказывают второй и третий факторы. В процессе экспериментального определения тепловыделения цементов на­ходят общий тепловой эффект перечисленных выше процессов. Рекоменду­ется [1] использовать данные о тепловыделении чистых клинкерных це­ментов из табл. 5.5. Отсюда следует, что чем ниже марка цемента, тем меньшей экзотермией обладает цемент.

Расчет показывает, что при адиабатических условиях гидратации вяжущий материал типа водного раствора портландцемента марки 600 вследствие действия внутренних источников тепла может саморазогре — ваться до температуры 180°С. Однако в условиях скважины явление саморазогрева может существенно осложняться в связи с дополнительны­ми затратами тепла на прогрев продавочной жидкости и окружающей породы, поэтому температура вяжущего может значительно отличаться от указанного выше значения.

Цемент

Тепловыделение, кДж/кг, через время, сут Марка —

TOC o "1-5" h z Глиноземистый 500—600 420 525 545

Глиноземистый 400 380 420 460

Портландцемент 600 300 500 545

Портландцемент 500 ‘ 250 420 485

Портландцемент 400 200 250 400

Пуццолановый 400 145 250 330

Тепловыделение обычно играет положительную роль, которая прояв­ляется в том, что теплота экзотермической реакции способствует допол­нительному разогреву вяжущего материала. По этой причине искусствен­ный камень набирает необходимую прочность за более короткий пе­риод. Отмечается также, что чрезмерное тепловыделение может привести к снижению качества цементирования, в основном вследствие дополни­тельного таяния мерзлых пород или льдов. На этот вопрос обращают вни­мание как советские, так и американские исследователи [74, 77].

Некоторые вопросы температурного режима вяжущего материала в изотермических условиях скважины рассмотрены в ряде исследований. Однако термический режим и кинетика превращения вяжущего суще­ственно зависят от температуры.

При решении такого типа задач встречаются существенные матема­тические трудности, поэтому количество аналитических решений крайне невелико. В литературе известно решение некоторых частных задач не­изотермического тепловыделения плоских тел, а также более общее иссле­дование [11].

Цель данного раздела заключалась в исследовании температурного ре­жима и кинетики превращения вяжущего в неизотермических условиях скважины, в интервале пород с положительной температурой. Получен­ные результаты можно использовать для исследования температурного режима цементного кольца в интервале скважины под толщей мерзлых по­род, а также в интервале мерзлых пород при нагреве цемента до нуля градусов. Другими словами, определять момент начала таяния стенок скважины. Особенность настоящего подхода состоит в существенном усложнении, поскольку возникает необходимость решения системы трех уравнений. Математическую формулировку задачи можно записать в ви­

dTt dt

(5.13)

де [55]

t = О, Т = 7’2 = Гз = 0; г = а, Г1 = 7*2, XdTi/dr = ХгдТг/дг г — Ь, Тг — Тъ, кгдТз/дг — ХздТз/дг; г = оо, Г3 = 0, дТз/дг = 0.

Индексы 1, 2 и 3 относятся к продавочной жидкости, вяжущему ма­териалу и горной породе соответственно. Таким образом, продавочная жидкость (вода или глинистая суспензия) заполняет центральную трубу радиуса а. Кольцевую трубу с радиусами а и b заполняет вяжущий ма­териал (обычно водная суспензия портландцемента марки 600). И далее скважину радиуса Ь окружают горные породы определенного типа. Другие обозначения: Т и а—температура и температуропроводность продавочной жидкости; 7г и а2 — температура и температуропроводность вяжущего материала; W — мощность внутренних источников тепла в объеме вяжу­щего; с2 и р2 — удельная теплоемкость и плотность вяжущего; Т3 и аз — температура и температуропроводность горной породы; t — время; Тп — естественная температура горной породы; A-i, А,2 и >,з — теплопроводность продавочной жидкости, вяжущего материала и горной породы; R — глу­бина проникновения тепла в горную породу; К — постоянная, характери­зующая химическую активность вяжущего данного типа; Ц — массовое содержание цемента в ёдинице объема раствора; G — полное количество тепла, выделяемое вяжущим; То и Т — начальная и избыточная темпера­тура вяжущего материала, а — степень превращения вяжущего в продук­ты реакции; to — масштаб времениз_С1 и qi — удельная теплоемкость и плотность продавочной жидкости; К и а" — постоянные коэффициенты; Fo = a3t/b2 — число Фурье.

R_ Ь ‘

Т3 = г—Лп-£-/1П- о

(5.15)

Под радиусом R понимаем расстояние от центра скважины до распо­ложенных на цилиндрической поверхности точек, начиная с которых тем­пература горной породы остается неизменной и равной начальному зна-

Задача (5.13) — (5.14) допускает только приближенное решение. При­меним способ, основанный на методе последовательной смены стационар­ных состояний и методе последовательных приближений. Метод последо­вательной смены стационарных состояний заключается в данном случае в том, что процесс разбивается на малые промежутки времени, в каждом из которых мощность внутренних источников тепла и температура вяжу­щего принимаются постоянными, а температурное поле в горной породе установившимся. Введем следующие допущения: 1) с целью упрощения задачи температурное поле в средах 1 и 2 принимаем равномерным, т. е. Т = Г2 = Т3 2) теплофизические свойства сред постоянны; 3) централь­ная труба расположена в скважине строго концентрично. В соответствии с вышеизложенным температурное поле в горной породе аппроксимируем выражением.

чению. Величина R является переменной и возрастающей с течением вре­мени. Обычно ее называют глубиной проникновения или радиусом влия­ния. •

Мощность внутренних источников тепла в объеме вяжущего мате­риала представим в виде

W = КЦйп^-а^То+Т). (5.16)

Аналогичная зависимость W от температуры использована в работе [21]. Анализ экспериментальных данных [20] показывает, что выражение (5.16) справедливо вплоть до значений степени превращения а = = 0,5-г0,6. Под степенью превращения понимаем отношение массы про­дуктов реакции к массе исходного вяжущего.

Для решения поставленной задачи необходимо определить две неиз­вестные величины: температуру и глубину проникновения тепла. Первое уравнение для определения неизвестных величин составим на основании следующего условия:

Введем безразмерные переменные Q = T/To; =R/b o=t/to X — = azto/b2. Подставляя в правую часть выражения (5.17) равенство (5.15) и выполняя соответствующие математические действия, получаем первое дифференциальное уравнение процесса

/_1Ы_ 1W6 ^ | £2-1 ч d% 9___

2ln| Vda+0V21n£ 4£ln2£7l£ ( ^

Второе дифференциальное уравнение получим из условия теплового баланса вида

KUGitb2-a2XTo+T) = [а2с10,-К&2-а^]^-2*Ьз&-^ | г_6. (5.19)

Подставляя в правую часть уравнения (5.19) выражение (5.15) и вы­полняя необходимые действия, получаем второе дифференциальное урав­нение процесса

—(m—n/ln£)9 = fii, (5.20)

где m = KUG(b2-a2)t0/C-, п = 2Ыо/С; С = [а2с, е1+(Ь2-а2)с2д2].

Из уравнения (5.20) получим

ln| = n е/[т(1 + в)-0′]: (5.21)

Отсюда находим.

I = ехр{7Г0/[т (1 +0)—O’]}. (5.22)

Дифференцируя (5.22) по о, получаем

t, ( Ш лвСтв’—в")) ( пв )

1 = 7^) ШГ~Jex*W-b (523)

где ‘ = d/da 8’= сШД/а; 8" = d2Q/do2 F(o) = т(1+в)-в’.

Таким образом, для определения температуры 0 необходимо решить уравнение (5.18) с использованием выражений (5.21) и (5.22) и с началь­ным условием 0 = 0 при о = 0. Эта система уравнений допускает только численное решение.

Возможен также иной подход, который позволяет без снижения точ­ности получить решение в замкнутой форме. С этой целью, перепишем уравнение (5.20) в форме

dQ/dl — х (l — ^S.) (I-1) 0 = x (I-1), (5.24)

где v. — 2Ь2т/(Каз); n = 2кз / c m = KU. G (b2—a2).

Решение уравнения (5.24) с начальным условием 0 = 0 при £ = 1 по­лучим в виде.

0 = 1+ ехр{ -|-(£-1)2 — — J-[Ei(2x) — Ei(x)j } X С

X S(П—1)ехр { ^£Ei(2x) — Ei(i)] — f (г,— if } rfn, (5.25)

где 0 = 1 — f 0; x = In £; Ei (x) — интегральная показательная функция. Переменные £ и т) соответствуют безразмерной глубине проникновения тепла и введены для пояснения порядка интегрирования. Переменная F соответствует величине In rj.

Использование решения (5.25) возможно при условии, что перемен­ная | является известной функцией времени. В соответствии с используе­мым методом решения £ можно найти в том случае, если известен закон изменения температуры вяжущего. Тогда задача сводится к численному решению дифференциального уравнения относительно неизвестной £.

Случай изотермического тепловыделения интересно рассмотреть, что­бы определить вклад неизотермичности в характер изменения темпера­туры вяжущего материала. Принимаем, что мощность внутренних ис­точников тепла постоянна и обусловлена только температурой Tq = const. Для определения температуры 0 в первом приближении принимаем, что £ изменяется так, как будто температура вяжущего в течение всего процес­са поддерживается постоянной. Нетрудно показать, что в этом случае за­кономерность изменения £ будет иметь вид

£=l+/^Fb, (5.26)

где К = 4.

Поскольку это соотношение определяет верхнее значение £, то подста­новка его в выражения (5.19), (5.26) или (5.25) дает верхнее значение 6.

Результаты расчета, представленные в исследовании [55], указывают на закон изменения температуры в форме

(5.27)

Т = а /Г

Используя второе приближение этого равенства, получаем дифферен­циальное уравнение относительно £, закономерность изменения которого имеет форму типа (5.26):

(5.28)

1=1+ /2FoT

Результаты расчета 0 из выражений (5.25) и (5.28) также представ­лены в исследовании [55] и подтверждают справедливость закона (5.27).

В случае неизотермического процесса закономерность изменения тем­пературы вяжущего вследствие дополнительного саморазогрева будет все более отклоняться от изотермического в сторону завышения. Измене­ние температуры вяжущего материала в первом приближении, аналогично изотермическому процессу, получим в случае использования выражений

(5.25) и (5.26). Результаты расчета температуры представлены в работе [55], причем закономерность ее изменения можно удовлетворительно аппроксимировать прямой линией вида

(5.29)

T = at.

Поскольку верхнее значение температуры вяжущего можно предста­вить в форме (5.29), то для определения закономерности изменения глу­бины проникновения во втором приближении использование выражения (5.29) тем более допустимо.

Для определения действительного значения £ в скважине конечного радиуса Ь приходим к дифференциальному уравнению, которое допуска­ет только численное решение. Ниже предлагается иной путь. Суть его за­ключается в том, что ^ находится после сопоставления закономерности изменения глубины проникновения в двух предельных случаях, когда Ь-*-оо и Ь-+0.

В случае Ь-*~оо принимаем координату г=Ь за начало отсчета, тогда вместо выражения (5.15) имеем распределение вида

(5.30)

Для определения R составим следующее соотношение: R

Т3 = T-Tr/R.

(5.31)

Подставляя выражение (5.30) в (5.31), приходим к дифференциально­му уравнению

„dR, ndT Т /соо,

Используя равенство (5.29), получаем вместо выражения (5.32) со­отношение

dR. R 2а3 ,сооч

ЧГ+~ /Г ( )

Дифференциальное уравнение (5.33) имеет форму Бернулли, которое путем подстановки R = /Г [27] переходит в линейное

dz 2 z

-Ж + ~Г = 4а* (5.34)

Решая это уравнение, имеем

R = Ь+ yW/3. (5.35)

В случае Ь-*~О для нахождения R составим уравнение вида

R

Тзгйг %зГЧг I ^°- (5.36)

Подставляя сюда выражения (5.15) и (5.29), получаем

dR | Ф(R) г. п„ 4<R) г — о7ч

‘dt + 2t R ~ 2аПГ’ (5 37)

где <р(/?) = (2lnR/b—l)/(2lnR/b).

Численный анализ показывает, что по мере увеличения R/b функция ф(/?) быстро стремится к единице, причем параллельно этому R стремится к верхнему значению. Полагая в уравнении (5.37) <р(£) = 1, получаем

" • * ** (5.38)

dt ^ 2t R ‘

Используя подстановку R — /Г[27], получаем линейное уравнение

dz 1 2 4а3. (5.39)

dt 1 t

Решение этого уравнения дает верхнее значение в форме

R = Ь+ УШ/3. (5.40)

Учитывая небольшую «вилку», R для скважины конечного радиуса будем определять из среднего, между (5.35) и (5.40), выражения

R = b+ yW/3. (5.41)

Обозначив Fo = a3//b2, представим это выражение в безразмерной форме

1=1+ /^Fo. (5.42)

Определив температурный режим вяжущего материала, можно рас­считать глубину экзотермической реакции, которая характеризуется сте­пенью превращения а. Степень превращения, которая согласно сделан­ному выше определению изменяется от 0 до 1, можно найти из выражения типа (5.16):

О

da = t0T0K § Qda. (5.43)

о

Подставляя вместо 0 выражение (5.25), совместно с (5.42), находим значение а.

Вычисление интеграла в выражениях (5.25) и (5.43) удобно выполнять при помощи формулы Гаусса для квадратур наивысшей алгебраической точности £

I ‘

§ КпМп =(п-)+-|-^( -1^2-)] • . (5.44)

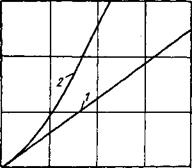
Временная зависимость степени превращения показана на рис. 5.4, где представлены результаты расчетов как без учета, так и с учетом тепло­выделения. Отсюда следует, что с учетом экзотермии можно получить зна­чительную экономию времени. Так, например, для a = 0,5 разница време­ни составляет 2 сут.

Представленные на рис. 5.4 результаты получены при следующих ис­ходных данных: К = 0,001 (ч-°С)-1 (по химической активности соответ­ствует цементу марки 600); Ц = 1200 кг/м3; а = 0,2 м; Ь = 0,25 м; Ciqi =

= £262 = 3770 кДж/(кг-°С); аз = 0,003 м2/ч; А,3 = 1,4 Вт/(м-°С);

То = 5°С.

SHAPE * MERGEFORMAT

О 25 50 75 100ч 93

Рис. 5.4. Изменение сте­пени превращения (гидра­тации) цемента во вре­мени.

0,1

1 я 2 — неизотермическое твердение без учета (/) и с учетом саморазогрева теплом гидратации (2).

Комментарии запрещены.