Бурение грунтовых зондов, установка энергетических колодцев

Поскольку гидравлические потери при прохождении потока через различного рода местные сопротивления не связаны с дли­ной, то их величина рассчитывается по формулам типа

р = aQ*y. . (III.25)

Местные потери давления можно определять и по теоретиче­ской формуле Борда — Карно для внезапного расширения:

= (vi — )2/2|? = £б ~2g ’

^(тг-ОЧтг-‘)2- (Ш’26)

где £б —1 коэффициент местных потерь из теоретической формулы Борда — Карно;, oi — средняя скорость до изменения сечения тру­бы; v2 — v—средняя скорость в трубе после местного сопротив­ления; ал и (02 — соответствующие площади сечения.

Однако практическое использование формулы (111.28) невоз­можно без внесения в ‘ нее некоторого поправочного коэффи­циента k, который определяется опытным путем и учитывает как влияние свойств движущейся жидкости, так и конструкцию самого местного сопротивления: ‘

= t £ = «в — (III.27)

Если сравним формулу (111.27) с формулой Дарси — Вейс — баха (III.20), то получим:

■ £ = Ujd, (III.28)

а имея в виду, что Я=/(Re, е), найдем, что коэффициент £ так же, как и коэффициент А, зависит в общем случае и от режима, и от состояния поверхности проходного канала, т. е. от шерохова­тости е.

Известны формулы Н. В. Френкеля, В. Н. Карева, А. Д. Альт — шуля и некоторых других авторов, в которых зависимость для £ дается в виде

£ = f (Re, dy/d. m), —

где dyldm — отношение диаметров наиболее узкой dy и широкой dm частей местного сопротивления.

Однако в реальных условиях конфигурация внутренних сечений по длине местного сопротивления (например, по длине замко­вого соединения) может изменяться несколько раз, что требует внесения определенных корректив, хотя бы в виде некоторого поправочного коэффициента а перед отношением dyjdm. Но для различных местных сопротивлений, имеющих одно и то же значе­ние dy/dm, но иную конфигурацию проходного сечения, значения такого поправочного коэффициента а могут оказаться разными. Поэтому вообще поиски зависимости именно от «самого узкого и широкого сечений» есть чисто формальная операция, так как при сложной конфигурации внутреннего сечения того или иного местного сопротивления применение принципа Борда, имеющего в виду только внезапный переход от узкого сечения к широкому, по существу теряет всякий смысл.

■ Если прямолинейные участки потока чередуются с местными сопротивлениями, то общая потеря напора вдоль всего трубопро­вода определяется по так называемому принципу наложения потерь, который сводится к следующему. Потери от трения и от местных сопротивлений определяются для каждого участка отдельно так, как будто они существуют самостоятельно. Затем найденные по­тери складываются и полученную сумму считают общими поте­рями от всех сопротивлений рассматриваемой системы. При этом для расчета потерь на трение берется Полная длина трубопрово­дов, включая и длину, занятую местными сопротивлениями.

Суммарные потери при этом согласно зависимостям (II 1.6), (III.20) и (III.27) могут быть выражены формулой. /Я/ и2

■ ■ Л*в(т + Ч)%- ‘ (IIL29)

В этой связи величину местных потерь выгодно определять так же, как и потерю напора на некотором как бы дополнитель­ном участке /э основного трубопровода:

*м = *£“!• (И1.30)

В данном случае длина /э называется эквивалентной длиной мест­ного сопротивления. Величины эквивалентных длин можно опре­делять из расчетов по известному коэффициенту £ для данного

местного сопротивления. Для этого, сопоставляя формулы (III.20) и (111.27), находим: .

— lB=Yd (IIL31)

и на основании полученной зависимости переписываем формулу

(III.29) в виде:

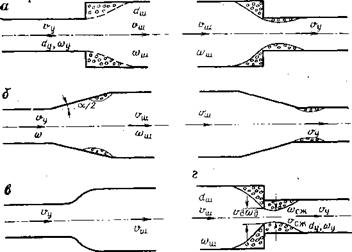
Рис. 7. Различные случаи расширения или сужения сечения: а — внезапное; б — постепенное; в — плавное; г — диафрагма

где величину /+24 = jL можно назвать полной расчетной или при­веденной длиной трубопровода.

Поскольку источником потерь может служить также и изме­нение нормального распределения скоростей в поперечном сечении, то в соответствии с этим необходимо считаться с некоторой по­терей энергии на так называемом входном или начальном участке трубы, где течение жидкости не успевает стабилизироваться. Только после этого участка можно вычислить потери на трение по рассмотренным ранее формулам. При определении же потерь на таком участке необходимо вносить соответствующие поправки с учетом их зависимости от режима течения.

Наконец, каждое местное сопротивление влияет на распреде­ление скоростей в потоке, что наблюдается на участке опреде­ленной длины до и после рассматриваемого местного сопротивле­ния. Поэтому принцип наложения потерь может быть применен только в том случае, если между отдельными местными сопротив­лениями будут расстояния, достаточные для формирования по­тока. ‘

В циркуляционную систему бурящейся скважины входит зна­чительное число элементов, в которых величина гидравлических

потерь может быть определена формулами типа (111.25) или (111:27). К ним в первую очередь должны быть отнесены замковые соединения бурильных труб, различного рода переводники, от­воды, вертлюги, задвижки и т. д. До некоторой степени сюда же могут быть отнесены стояки, шланги, турбобуры, электробуры и др. Поскольку для большинства из этих элементов характерным источником местных потерь являются потери, возникающие в связи

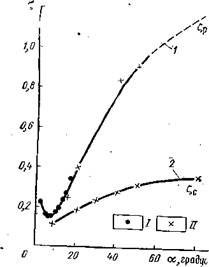
Рис. 8. График изменения потерь на расширение и сужение в зави­симости от угла конусности:

с изменением сечения потока, целе­сообразно рассмотреть этот вопрос детальнее.

Различают следующие случаи изменёния сечения: внезапное рас­ширение или сужение; постепенное расширение (диффузор) или суже­ние (конфузор); плавное сужение или расширение (сопло). Своеоб­разный случай изменения сечения можно наблюдать на примере диа­фрагм. Все отмеченные виды изме­нения сечений показаны на рис. 7.

Многочисленными эксперимен­тальными исследованиями доказано, что При всех прочих равных услови­ях потери при расширении всегда несколько больше, чем при сужении (рис. 8), и для этих случаев долж­ны применять различные формулы.- Так, для сужения (индекс «с») по­тока

3 г — расширение: 2 — сужение;

/ — по данным [14], II — по данным Тарасова — Агалакова

uv f 1 2

К = £с ‘ £с = Рс(—-l), (Ш. ЗЗ)

а для расширения (индекс «р»)

„2

^р — Ср 2g ‘ £р Рр 0 n)s>

где e = f(«); п=щ/сош; ® — площадь сечения (индексы «у» и «ш» обозначают величины, относящиеся к узкому и широкому сечениям соответственно); коэффициент |3 — фиксирует характер и степень сужения или расширения («внезапное», «плавное» и т. п.). Для случая диафрагмы (индекс «д»), показанной на рис. 7, г, расчетная формула имеет-вид (РСЖ °у)2 «. ву. — Эд о — ’ •

-‘)• ■ ®СЖ^СШ = Vy°b = U3®3 == » 8 — Фсж/®3 .

Лд —

2g

(111.34)

28 .= f Юу’ ‘ V <Пзе

(III.35)

так как 44

Если же диафрагма будет установлена таким образом, что на пути потока сначала будет труба малого диаметра, а затем боль — iHOro, то в формулу (II 1.35) ‘вместо скорости оу следует поставить скорость vm.

Для определения коэффициента сжатия известна приближен­ная формула, рекомендуемая А. Д. Альтшулем и П. Г. Киселевым

(111.36)

При плавном расширении (сужении) величину р должны нахо­дить по специальным графикам. В частном случае внезапного ^расширения (сужения) j3p = |3c=l. Величина потерь в диффузорах должна находиться как сумма потерь на трение и расширение, а в конфузорах — на трение и сужение. Однако чаще пб’таблицам’ или графикам (см. рис. 8) в зависимости от угла конусности а сразу определяют суммарные значения £дИф или £кон.

При конических переходах с плавным закруглением (сопло) потери значительно уменьшаются. В этих случаях Т. М. Башта [14] рекомендует принимать £ = 0,03 + 0,1 независимо от того, имеет место сужение или расширение потока. При этом делается оговорка: чем больше Re, тем меньше £. Авторы [1] считают, что в случае плавного сужения следует брать £=0,01+0,10. По данным И. Г. Есьмана, если угол конусности сопла а^5—7°, то потери будут близки к нулю. *

К числу местных гидравлических сопротивлений могут быть отнесены и сварные стыки труб [55], а также муфтовые соеди­нения.

Комментарии запрещены.