Бурение грунтовых зондов, установка энергетических колодцев

В тех случаях, когда по каким-либо причинам нет дифферен­циального уравнения для описания процесса, то отыскание необ­ходимой зависимости между величинами, характеризующими рас­сматриваемое явление, можно осуществить при помощи анализа размерностей (метод Релея). Для этого лишь необходимо твердо знать от каких именно величин зависит протекание процесса и выразить все эти величины в одной какой-либо системе единиц.

Еще Гаусс показал, что поскольку все физические законы выражаются уравнениями, устанавливающими зависимость между различными физическими величинами, то, выбрав некоторые (любые) из этих величин как основные (независимые) и устано­вив для них единицы измерения, можно выразить через них еди­ницы измерения всех остальных (производных) величин. При этом любая физическая величина А может быть представлена в виде произведения. ‘

А = kXpYqZr, (IV.26)

где X, Y, Z — физические величины, принятые за основные (неза­висимые); р, q, г—целые или дробные, положительные или отри­цательные числа; k — коэффициент пропорциональности.

Формула размерности может иметь и другое применение. Так, сравнивая размерности левой и правой частей какой-либо, формулы и обнаруживая отсутствие тождества, можно с уверен­ностью утверждать, что рассматриваемая формула противоречит — физическому смыслу исследуемого процесса (явления) и, следо­вательно, неверца в принципе.

Еще более важное значение анализ размерностей приобретает в связи с возможностью использовать его для непосредственного вывода формул. Рассмотрим, например, истечение жидкости иа сосуда с постоянным уровнем в среду с дарлением, равным дав-

лению на свободной поверхности. Если пренебречь сопротивле­нием движению, то средняя скорость истечения v зависит от уско­рения свободного падения g и высоты напора h. Следовательно, в общем случае зависимость между этими величинами может быть представлена выражением v = f(g, h). ‘

На основании анализа размерностей эту формулу можно за­писать в виде v = mg? hb

или, учитывая размерности входящих в нее величин,

LT~l = mLaT~2aLb,

где т — коэффициент пропорциональности, определяемый из опыта. — ‘

Так как, согласно ранее изложенному, для правильного отобра­жения физической сути явления должно соблюдаться условие равенства показателей степени при однородных величинах в обеих частях любой формулы, имеем для L: 1 =а + 6 и Для’ Т: —1=—2 а.

Решая эту систему уравнений, найдем, что а = Ь = 1/2. С учетом найденных значений определим v = mg1/2hl/2 = m~[/gh.

Значение m известно из опыта: оно приблизительно равно 1,41. Тогда

# v=y2gh,

т. е. получается известная формула Торичелли, найденная им для идеального случая, (см. § 1, гл. V).

Я. М. Брайнес рекомендует способ, позволяющий совершенно просто получать любые критерии подобия из соответствующих формул размерности. Для этого, имея формулу размерности какой-либо физической величины, достаточно разделить левую часть на правую, перевести полученные величины в коэффициенты (множители) преобразования и затем выразить их через основ­ные единицы измерения. Так, например, для размерности массы в системе МКГСС это дает:

I m I L kmki ml

. m — L—iFT2; !—=1; -2-i-=i; ——————— = idem.

FT2 ‘ kFk2 Ft2

Или имея в виду, что v = l/t, . ■

mv/Fl — — idem.

Сравнивая полученное выражение с (IV.7), убеждаемся, что полу­чен критерий Ньютона в «перевернутом виде», т. е.

1/Nu= mv/Ft.

Аналогично могут быть получены и другие критерии подобия. Следует, однако, помнить, что один только метод анализа размер­ностей не дает возможности наметить граничные условия и выде­лить определяющие критерии. Для этого обязательно надо знать уравнение процесса.

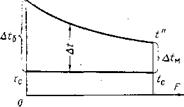
В состав почти всех критериев входят те или иные величины,, которые изменяются под воздействием температуры. Следова­тельно, важно условиться о некоторой единой, определяющей температуре, по которой можно было бы рассчитать все эти вели­чины для всех критериев. За такую температуру может быть при­нята средняя по длине трубы температура жидкости taк, которая находится по формуле

*ж = *с±Л*, (IV.27>

где tc — температура стенки в рассматриваемом сечении; Ait — среднее значение температурного напора.

Знак плюс берется при охлаж — „ ;г дении жидкости, знак минус — при

ее нагревании.

В соответствии с обозначениями на рис. 12 для температурных напо­ров на противоположных концах трубы имеем

A = t’ — tf", Д/м t" — fc.

Если Д^б./А/М^1,7, то средний температурный напор может быть

„ т- . определен как среднеарифметиче-

TOC o "1-5" h z Рис. 12. График изменения тем — » г

пературного напора вдоль трубы СКИИ

при /c = const и a = const • At<4-Atv

At = Ata =——- ______ — . (IV.28>,

Если же А/б/Д^м> 1,7, то необходимо йользоваться только средне­логарифмическим напором Д^л: 1

At6 — AtM

At = At„= . ‘ (IV.29)-

. шД^Д/м

‘ щ • ‘

Влияние резкого изменения значений физических параметров в пограничном слое учитывается особым безразмерным парамет­ром. В качестве такого параметра, по предложению М. А. Ми­хеева, принимается отношение значений критерия Прандтля Рг, выбранных по температуре жидкости tm и температуре стенки tc в степени 0,25, т. е. (Ргж/Ргс)0’25. ,

Комментарии запрещены.