Бурение грунтовых зондов, установка энергетических колодцев

Вследствие весьма сложного механизма движения турбулент­ного потока вывести зависимость между расходом и давлением при этом режиме чисто теоретически не удается даже для ньюто­новских жидкостей. Среди полуэмпирических теорий турбулентно-

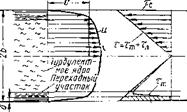
сти наибольшую известность получила теория Прандтля— Карма­на, согласно которой турбулентное течение рассматривается как течение, в среднем установившееся: скорость в каждой точке про­странства, хотя и изменяется со временем, в среднем остается постоянной для любого достаточно большого промежутка време­ни. Для такого потока характерно наличие поперечных движений отдельных частиц жидкости, кото­рые наблюдаются в виде пульсации скоростей. В свою очередь, наличие пульсаций скоростей обусловлива­ет появление дополнительных каса­тельных напряжений тт, численная величина которых должна опреде­ляться из зависимости

Ламинарный подслой

Рис. 24. Схема распределения скоростей и касательных напря — " турбулентном потоке

/ ди 2 du

=<“‘Ы)=А^" <у, эд

женин в

Это соотношение называют урав­нением Прандтля. Здесь I — неко­торая величина, которую Прандтль назвал длиной пути перемешивания.

и указал, что она по своему численному значению пропорциональ­на расстоянию у от стенки трубы, т. е. ‘

1 = (VI.22)

Коэффициент % был признан не зависящим от свойств жидко­сти и назван (Карманом) универсальной постоянной.

Сумма вязких напряжений и дополнительных касательных дает полное касательное напряжение в турбулентном потоке (рис. 24):

(VI. 23)

ди. ди ди

1"5T“<fl+ ’

Величина А по своей структуре формально совпадает с форму­лой (II.6), в силу:, чего она и получила название турбулентной вязкости, которая отличается от обычной тем, что изменяется при переходе от одной точки потока к другой, стремясь к нулю при приближении к стенке. Кроме того, она по своей численной вели­чине значительно превосходит обычную вязкость, особенно при больших скоростях. Это позволило Прандтлю принять, что при турбулентном режиме в формуле (VI.23) первым членом можно пренебречь и с учетом значения А из (VI.21) получить

Т — Тл -|- Тт — (1 ■

ди ду

= I

(VL24)

Исходя из размерности величины Ут/р, Прандтль назвал ее «динамической скоростью» и предложил обозначать буквой г*. С учетом сказанного и подставляя значение I из (VI.22) в выра­жение (VI.24) , можно получить:

/————- ии

(VI. 25)

v* = Ут/р

dy

Проинтегрировав выражение (VI.25), Прандтль получил зави­симость для текущей скорости, в которую, однако, входят две так называемые универсальные константы, не поддающиеся определе­нию теоретическим путем. Численные значения этих универсаль­ных констант Прандтль определил исходя из обработки данных опытов Никурадзе и в конечном счете нашел расчетные формулы для профиля скоростей и коэффициента трения для гладких и вполне шероховатых труб. Две из этих формул приводятся ниже:

‘ ^=- = 21gReVX-0,8; (VI.26)

1 d 3,7d

w = 2,gT+l,14 = 2,g—. (V. .27,

J

Формула (VI.26) предназначена для области гладкого трения (гладкие -/рубы), а формула (VI.27) — для области квадратичного трения (вполне шероховатые трубы). В формуле (VI.27) k обоз­начена абсолютная шероховатость.

Для переходной зоны, которая для труб с естественной шерохо­ватостью является чаще всего рабочей областью, расчетных фор­мул Прандтлем предложено не было. Такую зависимость впервые установил Кольбрук, механически объединив для этой цели фор­мулы Прандтля для гладких и вполне шероховатых труб. Полу­чить аналогичную формулу аналитическим путем удалось

А. Д. Альтшулю [1] при условии, что турбулентный поток необ­ходимо рассматривать как единое целое и нельзя пренебрегать динамической вязкостью р в (VI.23): *

1 / 2,5 k

= ~21g( ‘/г +Т7Г • (VI-28)

1/Х s ReVAT ^ 2,8d

При условии, что k = 0,76 ka, зависимость (VI.28) полностью совпадает с формулой Кольбрука/а после ряда допущений может быть приведена к значительно более удобному для расчетов виду

TOC o "1-5" h z = l,81g——————— .————————— (VI. 29)

У1 Re —+ 7

‘ d

Еще более удобную зависимость А. Д. Альтшуль получает, за­меняя логарифмическую формулу (VI.29) степенной;

/ k, 100 ,25

Я“0,1 (~d“ +-5г) ‘ <v,’30>

где ki — 1,46 kg’, k3 — эквивалентная шероховатость (см. с. 41).

Известны попытки применить идеи Прандтля — Кармана и для случая турбулентного течения глинистых растворов [44 и др].

При этом наиболее простая формула (при условии, что A/d — = 0,001 =const) была получена Н. П. Лещим и Д. Ю. Мочернюком:

’ 0,482 ‘ ‘

Я = 0,018+ (Re;)0,46e • (VI.31)

Нами была предпринята попытка использовать схему вывода Прандтля—Альтшуля таким образом, чтобы получить формулу, аналогичную формуле (VI.48), но пригодную как для ньютонов­ских, так И для вязко-пластичных жидкостей. Для этого исходное выражение (VI.23) для касательного напряжения было представ­лено в виде

т = (т, + Л)-^-+т0. (VI.32)

— ау

Далее, повторяя схему вывода А. Д. Альтшуля [1], в конеч­ном счете было получено следующее выражение:

313

0,889л в.

, / кг 100

100 ,25 v2р

£ = — =Яш, (VI.33)

где п — поправочный коэффициент, определяемый из опыта.

Однако при выводе зависимости (VI.33):, значения коэффици­ентов турбулентности аир были взяты из опытов Никурадзе и приняты постоянными. Как указывает Уилкинсон, в исследованиях Доджа и Метцнера было выявлено, что первая константа турбу­лентности а в формулах для ньютоновских жидкостей, до сих пор рассматривавшаяся как универсальная постоянная, в действитель­ности является всего лишь некоторым значением непрерывной функции в точке. Учитывая это замечание, мы несколько видоиз­менили окончание вывода и нашли следующее выражение для X:

> «.«* (VI. 34)

дД — mbi 151fea kx ^

а » d

где т~ ; Ь и &2ч— опытные коэффициенты.

1 — 308/1? ш

Полученное выражение при То=0 обращается в формулу (VI.29) и тогда а = 0,4; р = 7,8; 6i=0,113; 62=0,421; т=ар = 3,12; ет=22,65.( В общем случае найденная формула позволяет выявить зависимость коэффициента К От обеих констант турбулентности (а и р), а также от параметра Rm. Однако окончательная пригод­ность зависимости (VI.34) может быть установлена только после экспериментальной ее проверки.

Работа [38] является по существу первым серьезным экспери­ментальным исследованием турбулентных потоков вязко-пластич­ных жидкостей. Использование в опытах современной аппаратуры
позволило авторам [38] подтвердить правильность предположения о том, что переход к турбулентному состоянию связан с появлени­ем поперечных пульсаций скорости, которые возникают вблизи стенки трубы при числах ReKp, достаточно близких к их значени­ям, определяемым зависимостью ReKp(He).

0,3164

Для ньютоновских жидкостей до сего времени не потеряла своего значения эмпирическая зависимость Блазиуса для гладких труб, которая дает удовлетворительные результаты при значениях Re от 2500 до 70 000 и имеет вид

(VI. 35>

Для области шероховатого трения (автомодельная зона при Re>1000 г’) наибольшую известность получила формула Б. Л. Шифринсона:

VI.36;

/1

Я, = 0,11 (kjd)0’25.

Для смешанной зоны предлагались формулы И. А: Исаева,

В. И. Черникина, Н. 3. Френкеля, Ф. А. Шевелева, упоминавшая­ся уже формула А. Д. Альтшуля и др. Приводя все эти формулы к унифицированному виду и сопоставляя между собой, нетрудно обнаружить, что формулы А. Д. Альтшуля и Ф. А. Шевелева на­много проще остальных, так как в них искомый коэффициент да­ется в явном виде и не имеет степени. Однако формула Ф. А. Ше­велева получена в результате опытов с новыми стальными водо­проводными трубами и учитывает в неявном виде шероховатость только этих труб. В формулу же А. Д. Альтшуля шероховатость входит как самостоятельная величина, в силу чего этой формуле следует отдать предпочтение, как наиболее простой и универсаль­ной.

Накопилось достаточно большое количество эмпирических фор­мул и для таких жидкостей, как глинистые и цементные растворы. Все они условно могут быть разбиты на две большие группы: двух — и одночленные. К первой группе относятся формулы Б. Д. Бакланова, Геррика, К. А. Царевича и А. И. Малыщева, П. П. Шумилова, В. П. Гайдукова,.Р. И. Шищенко и др. В их ос­нове лежит формула Вильямса—Хазена, которую Геррик предло­жил привести к виду

(VI. 37)

Идея Геррика, заключающаяся в том, что гидравлические по-

тери при движении глинистых растворов могут быть выражены как сумма давлений, идущих на преодоление сил предельного напряжения сдвига и вязкостного трения, оказалась весьма плодотворной и до сих пор используется некоторыми ис­следователями. Однако во всех этих формулах, включая и формулу Геррика, входящие в них коэффициенты (с,

k и т — п.) определяются для каждого данного раствора, что намного снижает их ценность.

Другая группа зависимостей построена по типу одночленной формулы Дарси — Вейсбаха. Сюда должны быть отнесены: фор­мула Ханока, полученная в результате обработки опытных данных Грегори, а также формулы Р. И. Шищенко и Б. Д. Бакланова; Р. И. Шищенко и А. X. Мирзаджанзаде; Б. С. Филатова; Б. И. Ми- тельмана; Р. И. Шищенко, К. А. Ибатулова и др.

В настоящее время в качестве расчетных зависимостей, как правило, используются одночленные. При этом основная труд­ность заключается в определении коэффициента Я. Среди зависи­мостей, предназначенных для определения этой величины, наи­большее распространение получили формула Б. И. Мительмана:

0,08

Я = ~1г——— , (VI. 38)

УКё*

которая пригодна в пределах изменения Re* от 2500 до 40 000, и формула Р. И. Шищенко и К. А. Ибатулова:

*■= Г075 » (VL39)

yTRe* ‘

которая рекомендуется для диапазона изменения Re* от 2500 до 50 000. .

Для значения Re* >50 000 значение Я обычно принимается по­стоянным и равным 0,02.

Нетрудно заметить, что обе приведенные выше формулы по своей структуре повторяют формулу Блазиуса для гладких труб с отличными, однако, значениями постоянных в числителе А и по­казателей степени т при обобщенном параметре Рейнольдса:

Я = 4(Re*)-m. (VI. 40)

Серьезный недостаток этих формул заключается в том, что они при значениях то=0 не переходят в формулу для воды, т. е. в фор­мулу Блазиуса. Между тем при то=0, Re* = Re такой переход должен соблюдаться. Указанное дает пбвод утверждать, что по своей структуре все рассмотренные формулы являются неверными или справедливыми только для каких-то определенных условий.

Исследуя этот вопрос, Э. К. Латыпов и Б. С. Филатов проана­лизировали обширный материал, полученный как отечественными, так и зарубежными авторами, и пришли к следующим важным выводам.

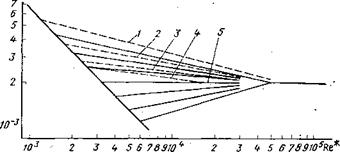
Оказалось, что в области переходного режима зависимость Я = /(Re*) для различных растворов неодинакова и образует на гра­фике пучок кривых (см. рис. 25), который сходится при значениях Re* = 3-7-6-104. Приближенно этот пучок может рассматриваться как пучок прямых, каждую из которых можно выразить формулой типа (VI.40). При этом величины Лит оказываются зависящими от ReKP и Ят;

Re* = Re/(1 -}- T0d/6rp)].

В свою очередь, величина Re^, зависит от реологических свойств бурового раствора и от диаметра трубопровода. Было найдено, что минимальные значения ReKp наблюдаются у раство­ров, имеющих малые то и большие rj, а максимальные ReKp — у растворов, обладающих низкой вязкостью и высокий напряжени­ем сдвига. Чем больше диаметр труб, тем при больших значениях

Л Рие. 25. Различные выражения зависимости — Я от Re* в пере­ходной области для круглой трубы: 1 — по Блазиусу; 2 — по Р. И. Шищенко; 3 — по Р. И. Шищенко и К. А. Ибатулову; 4 — по Б. И. Мительману; 5 — по Б. С. Филатову

Re^p происходит переход от структурного режима к переходному. Исходя из изложенного Э. К. Латыпов и Б. С. Филатов составили таблицу соответствующих значений Re^, А и т и. рекомендовали ее к использованию. Однако позже Б. С. Филатов [61] счел воз­можным несколько сократить эту таблицу и увязал значения коэффициентов А, т и Я с реологической характеристикой бурово­го раствора (табл. 5). Таким образом, в диапазоне 2000<Re*< <50000 значение Я в зависимости от типа раствора находится по формуле Я=A (Re*)m. ,

Таблица 5 Тип раствора р, г/см* Т), Па-с т„, Па А т Неутяжеленный Утяжеленный Утяжеленный 1,4 (Т <50 с) 1,4—1,75 1,8 0,005—0,020 0,010—0,030 0,015—0,045 10 5—20 9—40 0,1 0,02 0,0025 + 1 ООО ьъг- о сл о

Отметим тот факт, что ни одна из формул, рекомендованных для определения Я при движении вязко-пластичных жидкостей, в отличие от аналогичных формул для ньютоновских жидкостей не учитывает фактор шероховатости. Наряду с этим следует иметь в виду, что шероховатость бурильных труб может меняться не толь­ко в зависимости от материала (стальные, ЛБТ) и способа изго-

Характеристика труб			Типоразмер труб
Н-114	В-127	н-	140	ЭБШ	ЭБШ
Наружный диаметр, мм	114	128	141	146	168
Толщина стенок 6, мм	10	8	9	10	9	9	11	10
Внутренний диаметр, мм	94	98	110	121	123	128	146	148
Коэффициент эквивалент — гной шероховатости труб
новых заводских	0,046	0,054	0,059	0,042	0,048	0,057	0,034	0,046
новых с коррозией	0,279	0,211	0,226	0,214	0,221	0,233	0,198	0,234
новых, находящихся в	0,382	0,367	0,314	0,347	0,374	0,405	0,356	0,389
эксплуатации						0,541	0,584	0,618
корродированных в ус­ловиях эксплуатации	0,503	0,443	0,523	0,946	0,572 *

товления, но еще в большей степени и от условий хранения и эк­сплуатации. Для подтверждения сказанного в табл. 6 сведены значения эквивалентной шероховатости ka в зависимости от со­стояния труб (по данным И. Р. Бунятова и Б. И. Есьмана).

Комментарии запрещены.