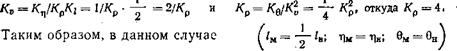Бурение грунтовых зондов, установка энергетических колодцев

При исследовании вязко-пластичных жидкостей Бабат и Колд — вел предложили использовать параметр Рейнольдса, в который входит не динамическая р. или структурная ц, а эффективная вяз­кость г’. В нашей стране этот параметр впервые был применен Р. И. Шищенко и А. X. Мирзаджанзаде и получил название обоб­щенного параметра Рейнольдса Re’. С учетом использования этого параметра вместо (IV.37) получим

vdp

(IV. 40)

Eu — j — — f (е, Re’); Re’ =

, Однако нахождение величины Re’ затруднено тем, что нельзя ■определить значение входящего в него градиента скорости dujdr без определенных допущений. Так, например, Бабатом и Колдве — лом принималось, что dujdr = Qv/d; Р. И. Шищенко, А. X. Мирза — джанзаде полагали, что эту величину следует брать равной 2v/d.

Э. К. Латыпов и Б. С. Филатов исходили из предположения, что dujdr = 8v/d. Заметим, что упрощение выражения для гра­диента скорости равносильно аппроксимации величины f(p), кото­рую они ввели для записи точного выражения обобщенного пара­метра Рейнольдса Re**: •

Re** = Re / (P); / (p) = 1 —-i — P + 4 P4: Р = <1У‘41>

о о а

где rf0 — диаметр ядра потока; d — диаметр трубы.

Предложены следующие аппроксимации для /(р): 1-^-4/ЗР; 1—4р; 1—Р; 0,855—Р; 0,38—0,4р. Первые три из них равносильны первым трем приведенным выше упрощенным значениям вели­чины dujdr. В то же время’ использование таких значений /(р) приводит к следующим выражениям для Re* соответственно:

Известно и другое направление, при котором упрощение дости­гается за счет принятия эмпирической зависимости типа ц’ = ац, причем величина а рекомендуется равной 3,2 (Бек, Нас, Дан)1; 1,5 (Хедстрем); 1 (Ван-Ольфен) и т. п.

Однако всех отмеченных трудностей можно избежать, если

в физическом уравнении (IV.34) заменить р, на т] и дополнительно

ввести т0. Тогда по аналогии с (IV.34) — (IV.37) получим:

f(d, Д, v, pH, р, т), т0) = 0; (IV.34а)

ф(ях, я2, л3, я4) = 0; (IV.35а)

Чт-

d x? pl vdp

—, —^. — 1 = 0; (IV. 36а)

pd р т0 / ‘

Ей — у- = /(е, В, Re), (IV.37a)

где 5 = о2р/то — обозначение четвертого я-члена, по своей сущ­ности представляющего отношение сил инерции к силам пластич­ности и поэтому названного критерием (параметром) пластич­ности. . •

Из выражения (IV.37a) вытекает, что для характеристики дви­жения вязкО-пластичной жидкости обойтись только одним пара­метром Re невозможно. В этом случае обязательно должен участ­вовать и параметр пластичности В, так как в данной ситуации оба эти критерия являются основными и определяющими.

Аналогичные выводы могут быть получены и без я-теоремы. Так, Р. И. Шищенко пользовался методом масштабных множи­телей. Н. В. Тябин тот же результат получил путем приведения к безразмерному виду им же выведенного уравнения вязко-пла­стичной среды. • .

В дальнейшем Н. В. Тябин установил характер функциональ­ной зависимости (IV.37а). С этой целью, умножая зависимость (11.12) на площадь, выраженную через характеристический раз­мер системы /, он получает выражение для силы сопротивления вязко-пластичной жидкости в виде

F = xl2 — т0/а + г(IV. 42)

, dr

а затем подставляет это значение F в выражение (IV.7). При ус­ловии, что т = р13, и допуская, что порядок du/drmv/l,[10] получает окончательно

Ne* = Б = + —V =А + ,. (IV.43)

pv2 pvl Re

Тем самым устанавливается аддитивный характер, функциональ­ной зависимости критерия Ей от Re и А, что позволяет записывать критериальное уравнение (IV.37a) в виде

Eu = /(£) = /i (Re) + U {А). (IV.44)

Легко показать, что параметр Б представляет собой не что

иное, как обратную величину точного обобщенного параметра

Рейнольдса. В самом деле, применяя к выражению (11.13) схему получения критериев (см. с. 55), получаем последовательно:

TOC o "1-5" h z т) x0dr Tt x0l

1)1 = —— — р———— ; 2) 1 = —— +————- ; 3) Производим замену величин ri и г]г

г)’ г du г]’ х’и.

на соотношение г] = u/p/Re и т’ —vlp/Re’. Тогда из 2) получается:

Re’ ‘ R-e^_ 1; 4) Re’ ‘ —

Re o2p ’ 1/Re А Б

Таким образом, по сравнению с движением вязкой жидкости условия моделирования процесса движения вязко-пластичной жидкости в значительной мере усложняются, так как в этом слу­чае должно соблюдаться подобие не одного, а одновременно двух каких-либо критериев:

Eu = idem; Re = idem; А = idem, (IV.45)

Между тем соблюдение подобного требования не всегда воз­можно. Для того чтобы убедиться в этом, рассмотрим несколько видоизмененный пример, приводимый в одной из работ В. Н. Тя — бина. Пусть имеется модель, по своим геометрически^ размерам в 2 раза меньшая, чем натура. В качестве рабочей жидкости на модели и в натуре предполагается использовать одну и ту же жидкость, имеющую плотность р, вязкость т) и динамическое на­пряжение сдвига т0. Выясним, будет ли при этом соблюдаться условие полного моделирования? В этом случае согласно (IV.45) должны соблюдаться два равенства:

°мРм^м °нРн^н Им °мРм^м

————— =———— , откуда = — ;

. Г)м ‘Пн — Пн инРн*н

ем 0я 0м Рм^м

откуда

Рм^ Рн^’н 0Н Рн”н

Если ввести множители • подобия (Kv = vMfvB-, Ki = luflн;

Кц =Пм/Пн; кр =рм/рн), то эти два равенства можно переписать иначе, а именно:

= КрКЛг, Ke = KpK2v. (IV.46)

По условию примера должно быть: /Сг=1/2; /Сч=1; /Ср=1; /Се =1. Подставляя эти значения в (IV.46), находим, что согласно’

первому равенству 1 = 1 — Kv-1/2, откуда Kv = 2; а согласно вто­

рому равенству = 1-Kl, откуда Kl =1. Таким образом, для Kv получаются противоречивые значения, что свидетельствует об от­сутствии полного подобия в данной ситуации.

Какими же свойствами должна обладать жидкость на модели,, чтобы условия динамического моделирования полностью соблю­дались? Рассмотрим несколько вариантов.

1. Если Ki=l/2; Kr = 1; Kp = , то на основании (IV.46)

Kv = KnIKpKi= 1/1 • 1/2 = 2 и Kq — KpKl = 1 -22=4. Таким образом,

если /м=1/2/н; г)м=т]н; pM = pH, то динамическое напряжение сдвига у модельной жидкости должно быть в 4 раза больше, чем у жидкости в натуре.

2. Если Ki= 1/2; /Ср =1; /Се = 1, то на основании (IV.46)

/С» = — Ке/Лр = 1/1 = 1 и /С») —KvKp Ki= 1 • 1 • 1/2= 1/2, т. е. в этом

случае (/м — 1./2/н; Рм —рн‘, 0м = 0н) вязкость модельной жидкости должна быть в 2 раза меньше, чем у жидкости в натуре.

3. Если /Сг= 1/2; /Сл = 1; /Се = 1, то на основании (IV.46)

плотность модельной жидкости должна быть в 4 раза больше, чем у жидкости в натуре.

4. Если бы в натуре протекала не вязко-пластичная, а вязкая жидкость, то для соблюдения полного динамического подобия на той же модели достаточно было бы соблюдения лишь первого равенства (IV.46), т. е. создания на модели скорости движения той же жидкости в 2 раза большей, чем в натуре. Если же на модели протекает жидкость, вязкость которой была бы, например, в 2 раза меньше вязкости натуральной жидкости, то для соблю­дения полного подобия надо было бы скорость на модели довести до скорости на натуре:

Вполне понятно, что для модели с другими множителями подо­бия все расчеты должны быть иными.

Говоря о критериях, призванных характеризовать процесс дви­жения вязко-пластичных жидкостей, нельзя не отметить, что в этой части наблюдается отсутствие единой терминологии и обо­значений. Часто это приводит к неверному представлению о якобы чрезвычайно большом числе различных критериев. На самом деле это далеко не так. „

А. А. Ильюшин, обосновав вывод общего уравнения движения вязко-пластичной среды, одновременно показал, что в этом слу­чае подобие потоков должно характеризоваться двумя крите­риями— Hi = rvfQl и И2=Р/0. Первый из них фиксирует отноше­ние сил вязкости к силам динамического напряжения сдвигу; второй определяет отношение сил давления к силам динамиче­ского напряжения сдвигу.

По свидетельству Рейнера, Олдройд установил, что динами­ческое подобие определяется для бингамова тела двумя безраз­мерными критериями, а именно, числом Рейнольдса Re = ap//r) и числом Олдройда О = 0d/r]U//. .

Р. И. Шищенко и А. X. Мирзаджанзаде предложили критерий Rs = 0r/rju, который повторяет критерий О, но с тем различием, что

в него вместо характеристической длины I входит фиксированная’ величина г (радиус трубы), полученная как частный случай из. общего условия:

du dr

ср

Qdr Rs = —— при г]du

В. Н. Тябин обозначает критерий Олдройда S, называет его* критерием Олдройда—Ильюшина и утверждает, что он является производным, ибо S = 0 = Ql/i)V—A Re, где А = 0/ри2 — определяю­щий критерий, вытекающий непосредственно из теории размер­ности или я-теоремы.

Р. И. Шищенко обозначает Res комплекс i)Vfdxo■

А. X. Мирзаджанзаде [44] комплекс х011ци обозначает буквой /Г и называет параметром Сен-Венана—Ильюшина, а позднее этот комплекс под тем же названием обозначен «Sen». В работе Б. И. Мительмана и Г. Д. Розенберга комплекс xodfrv обозна­чен А.

TOC o "1-5" h z Таким образом, имеют место следующие соотношения: ,

= О = 2RS = S = Sen — ——- = = И.

щ s И, Rs

Учитывая, что в обобщенный параметр Рейнольдса рассмат — рйваемый комплекс входит именно как произведение xod/ци, пола­гаем, что его следует так и записывать, обозначая буквой И и на­зывать параметром Ильюшина.

Некоторыми авторами было предложено параметр* Re’ = Re/(l+ Rs) при условии, что Rs^l, называть параметром И. Г. Есьмана и обозначать буквой Е, т. е.

Re vdp-qv 2угр

Rs W

Р. И. Шищенко находит критерий, определяющий отношение сил пластичности к силам инерции, и обозначает его B=x0fpv2. Такого же обозначения нового критерия (В=xjpv2) придержи­ваются Б. С. Филатов, Б. И. Мительман и Г. Д. Розенберг.

В работе [44] этот параметр получает обозначение Re" и ему присваивается название параметра Рейнольдса. Такое же обозна­чение (без названия) встречается в других работах.

В работе [68] за комплексом v2p/xo утверждается название’ «параметр пластичности» и предлагается запись B*=v2р/то-

Таким образом,

TOC o "1-5" h z tflp 1 1 Е

—с — = Re" = — = — = — = В.

т0 А В 2

Однако, учитывая огромные заслуги Р. И. Шищенко в разви­

тии гидравлики глинистых растворов и тот факт, что он первый ввел термин «параметр пластичности», предлагаем в дальнейшем
последний назвать параметром Р. И. Шищенко и обозначить его буквами Rm

‘ Rm = i;2p/V (IV.47J

Помимо рассмотренных встречаются и другие параметры. Так, Р. И. Шищенко предложил критерий, определяющий наличие структурного режима в виде

Riy Diy р г т

* или А =———————— —————————

. 2» 4» р0 г0 т0

В дальнейшем этот же параметр (без изменения написания); Я — А. Шварц и А. X. Мирзаджанзаде предложили называть пара­метром Р. И. Шищенко и одновременно ввели новый комп­лекс— Bai—yl/Q, который назвали параметром Б. Д. Бакланова. Этот же параметр обозначен и как St//=y//xo. Он назван парамет­ром Стокса для пластичных жидкостей. Параметр Стокса для. вяз­ких жидкостей обозначен St=y/2/rjy2. ‘

Р. И. Шищенко показал, что при исследовании движения вязко-пластичных жидкостей может иметь место параметр Лагранжа La = pl/rv. Другие авторы этот же параметр называют параметром Лагранжа для вязких жидкостей, а второй параметр Ильюшина, т. е. И2=р/0, обозначают Ьа"=р/т0 и называют пара­метром Лагранжа для пластичных жидкостей. •

В последнее время все шире используют параметр Хедстрема, который может быть представлен как произведение параметров Ильюшина и Рейнольдса.

Не = И Re = ———— —( (IV.48)

‘ rv T]g — Ifg

По своей физической сущности параметр Хедстрема как бы уста­навливает взаимосвязь между свойствами жидкости и размерами канала.

Комментарии запрещены.