Бурение грунтовых зондов, установка энергетических колодцев

Как видно из выражения (111.13), для определения удельного теплового потока необходимо знать коэффициент теплопровод­ности материала, через который передается тепло, а также темпе­ратурный градиент. Для нахождения этого градиента нужно знать распределение температур, что в общем случае возможно лишь б результате решения дифференциального уравнения теплопро­водности: ’

или

дт ср

dt X

(III.37)

где а—коэффициент температуропроводности, характеризующий скорость изменения температуры; V2 — оператор Лапласа, пред­ставляющий собой символ, при помощи которого обозначают сумму вторых производных (в данном случае температуры) по коорди­натным осям; qv—производительность внутренних источников тепла.

Способы решения уравнения теплопроводности Фурье для раз­личных случаев разнообразны.

Если процесс передачи тепла происходит только в одном на­правлении, например в направлении оси х, то уравнение (III.37) упрощается и принимает вид

*=a™ + «L. (III.38)

дх дх2 ср

Если при этом процесс установившийся, т. е. dt/dт=0,

— =_— qv. (III.39)»

‘ дх2 X

Если внутри объема не выделяется тепло, т. е. qv = 0, уравнение (111.37) упрощается:

dt ( 34 дЧ т тг м

_ = av4 = a(_ + _+_j (Ш.40)

TOC o "1-5" h z или в цилиндрической схеме координат при условии, что тепловое поле обладает осевой симметрией.

, +J. JL+«Л. (III.4I>

дх дг2 г дг т дг-1 ) У

При установившемся тепловом режиме, когда dtfdт=0, выра­

жения (111.40) и (III.41) принимают вид:

‘ + + i?!L = о, (III.42)

дх2 ^ ду2 дг2 4 ‘

и ‘

дЧ 1 dt дЧ ‘ . #III

— +.———— — + — гг = °- — (И1.43)

дг2 г дг дг2

Таким образом, если температура исследуемого пространства. не изменяется во времени, то уравнение теплопроводности авто­матически переходит в уравнение Лапласа.

Решить уравнение Фурье в условиях неустановившегося ре­жима очень трудно и удается лишь в самых простых случаях.

Для решения задач, связанных с теплообменом в бурящихся скважинах, в. первую очередь должны быть выяснены качествен­ная и количественная характеристики явления передачи тепЛа через стенки бурильных и обсадных труб, участвующих в иссле­дуемом процессе.

Вначале примем, что колонна труб (бурильная или обсадная) имеет по всей длине I одинаковые наружный d2 и внутренний d диаметры и выполнена из материала, коэффициент теплопровод­ности которого равен А и постоянен для всех ее точек. Далее примем, что внутренние источники тепла, в колонне отсутствуют, температура изменяется только в радиальном направлении и под-

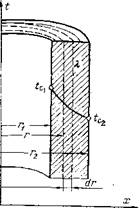
Рис. 9. Схема распреде­ления температуры в од­нородной цилиндриче­ской стенке

r% Л

In

(III.47)

9 F —

[1 rx ‘1 ‘ (111.45) Из полученного уравнения следует, что количество тепла, пере­данное через однородную стенку цилиндрической трубы в единицу времени, прямо пропорционально коэффициенту теплопроводно­сти Я, длине I, температурному напору (tCi —tC2) и обратно про­порционально натуральному логарифму отношения наружного ра­диуса г2 к внутреннему Г. Внутри однородной цилиндрической стенки температура изменяется по логарифмической кривой. Величина Q может быть отнесена либо к единице длины, либо тс единице поверхности, в результате чего будут получены раз­личные размерности. Так, если Q отнести к единице длины трубы I, то расчетная формула примет вид: ’ Q 2лЯ — 4l— ~~л 777“ А* [Вт/м],

а температурный градиент grad t — dt/dr, Подставляя найденные величины в урав­нение (111.11) Фурье, находим, что количе­ство тепла, проходящее в единицу времени через выделенный слой, будет Q = —XTgrad< = — Я2nrl-~ . (III.44) or • Интегрирование уравнения (111.44) с учетом граничных условий, согласно кото­рым — при r=r\ t=tCi при г=г2, в ко­нечном счете приводит к выражению „ 2л XI 2л Я! г_ а:= —— (‘с, — U = —:— ibtj

ndj/ d-i In d2/d1 Так как здесь. могут быть приняты и внутренняя (F=Fь <di=di) и внешняя (F=F2; d{=d2) поверхности, то значения удель­ных тепловых потоков qFt и qFi будут различны. Связь между Ци Яр* и qF, может быть определена из соотношения _ qi = nd1qFi = nd2qFi [Вт/м]. (Ш-48)

держивается постоянной и равной tCt на внутренней поверхности трубы и tc% на ее наружной поверхности, при этом tCl>tC2 (рис. 9). Выделим внутри стенки колонны кольцевой слой с внутренним радиусом г и толщиной dr. Тогда внутренняя поверхность этого слоя по всей длине колонны будет F — 2nd,

I ‘ In dj/d, если же Q будет отнесено к единице поверхности, то 0_ О 2ЯД< F

[Вт/м2].

(III.46)

In ■

Если случай более сложный, т, е. передача тепла осуществляется через цилиндрическую стенку, состоящую из нескольких слоев (рис. 10), при стационарном тепловом режиме через все слои будет проходить одно и то же количество тепла. Следовательно, в соответствий с выражением (111.47) для каждого слоя можно составить следующее равенство: 2я (‘с,-U Я1 =

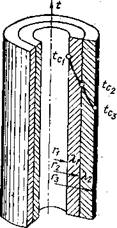
Очевидно, что суммируя перепады темпе­ратур для каждого слоя, т. е. складывая от­дельно все левые и все правые части системы уравнений, аналогичных (111.53) и (HI.54), можно получить полный температурный напор между внешней и внутренней поверхностями многослойной стенки. Так, для примера, изображенного на рис. 10,. при таком суммировании получим

■— ~г~ 1п 2я A-g )

_1_ К 2л (tCt

изменение

(III.52X

41 =

. ,___ Я_1__ J_ . А с» с’— 2п ‘

~ In dg/dg Ля. ‘

‘ ql f 1, 4 1 , d3

Рис. 10. Схема рас­пределения темпе­ратуры. в многослой­ной цилиндрической стенке

Из этих уравнений м’ожно найти температуры для каждого слоя

dx dg dg

*Сг

(111.53.

Зная полный температурный напор, нетрудно определить вели­чину теплового потока qr. .

2я (t — tc)

Яi = ————- ,— 1 г-……. — • (111.54)’-

1

i 1 i dз

In ■

+ Т“1п_Г

dr

Если представить изменение температуры в многослойной ци­линдрической стенке графически, то получим ломаную кривую. В то же время внутри каждого слоя температура будет изме­няться так же, как и при однородной стенке, т. е. по логарифми­ческому закону. ,

Если толщина стенки трубы мала по сравнению с диаметром (отношение d2/^i<2), то влиянием кривизны стенок обычно пре­небрегают. и теплопроводность трубы рассчитывают по формулам для плоской стенки. Формула для определения значения удельного’

потока, проходящего через многослойную плоскую стенку, имеет следующий вид:

TOC o "1-5" h z 61 # fyt. у, 8j.

A U.

Если тепло проходит через цилиндрическую трубу, то условия под­вода и отвода тепла всегда различны, так как внутренняя поверх­ность трубы всегда меньше наружной. .

Комментарии запрещены.