Бурение грунтовых зондов, установка энергетических колодцев

Если потеря напора hi вызывается только сопротивлением, рав­номерно действующим по длине потока I, то она должна равняться работе А некоторой силы трения Т, отнесенной к весу движущейся жидкости, т. е.

h[ — A/G. (Ш.15>.

При этом A = Tl, a G=y/(o, где w — площадь- живого сечения по­тока; у—удельный вес жидкости.

Полная же сила трения Т может быть представлена произве­дением площади S поверхности, по которой происходит1 соприкосно­вение жидкости (S = %1), на величину касательного напряжения на стенке тс, т. е. Г=тс%/, где х— периметр смачивания. Подстав­ляя найденные значения A, G и Т в (111.15), получаем:

Т Tell

= -£4-. . (111.16)

усо уаз

Величина xjy выражает фактические потери энергии на преодо­ление сопротивлений и является сложной функцией истинной скорости и, реологических свойств жидкости, состояния стенок и отношения со/х, представляющего собой гидравлический радиус RT, т. е.

Яг = ю/х — (111.17)

Из различных зависимостей для определения хс/у в условиях напорного движения наиболее рациональной оказалась формула Дарси, предложенная им на основании натурных опытов:

• тс/у = bv2/2g. (III. 18)

Подставлйя (III. 18) в (III. 16), находим:

h‘-bh%- . <iru9>

откуда видно, что величина Ъ не имеет размерности.

Если гидравлический радиус RT заменить его значением для

щ mP/t, d

круглых труб, т. е. подставить значение #г т = —,

то формула (III.19) примет вид: ‘

, 4 blv3

hi = •

2gd

< 1

Приняв 4Ь = Х, получим известную формулу Дарси — Вейсбаха:

*. = ^. (Ш20)

где X — безразмерный коэффициент гидравлических сопротивле­ний по длине.

Если из (III.18) определить тс и вместо b подставить Х/4, то получим два выражения, которые часто встречаются при иссле­довании вопросов, связанных с изучением движения жидкости в трубах:

тс=^—^- ^или0 = |/А j/^* (П1.21)

В американской литературе коэффициент b обозначается f и носит название «коэффициента трения в формуле Фанинга», т. е. / — Я/4.

В результате многочисленных опытов бйло установлено, что коэффициент X находится в сложной зависимости от многих фак­торов, в том числе от состояния поверхности (шероховатости) стенок трубы или канала, а также от характера движения (ре­жима) потоков.,.

Рейнольдс первым установил наличие двух различных режимов движения ньютоновской жидкости — ламинарного — без переме­шивания частиц (струй) и турбулентного—с перемешиванием струй потока, показав при этом, что переход от одного режима

к другому (и обратно) совершается при определенной скорости потока, названной им критической. ‘

Момент перехода ламинарного режима в турбулентный (и об­ратно) характеризуется определенным численным значением неко­торой безразмерной величины, впоследствии названной критиче­ским числом (параметром) Рейнольдса:

Vmd

ReKp = J2_ . (III.22)

v

Как показали дальнейшие многочисленные исследования, для ньютоновских жидкостей наиболее вероятно ReKP=2320.

Благодаря классическим трудам Прандтля, стало возможным дать четкое объяснение явлению смены режимов. Согласно его — идеям, твердые стенки, ограничивающие поток, являются теми поверхностями, которые создают основное направление всего дви­жения в целом. Пленка жидкости, соприкасающаяся со стенкой, прилипает к ней и остается неподвижной. По этому прилипшему, весьма тонкому слою скользит остальная масса жидкости со-ско­ростью, нарастающей от стенок К центру потока. Первые слои жидкости образуют так называемый пристенный слой, который скользит вдоль стенки, сохраняя ее направление. Течение в этом слое остается ламинарным даже в том случае, когда общий режим движения всего потока становится турбулентным. Толщина этого слоя очень незначительна — и зависит от состояния поверхности стенок, от вязкости и скорости жидкости. Так, при малых скоро­стях, когда существует ламинарный режим, толщина пристенного слоя оказывается достаточной для того, чтобы скрыть все выступы шероховатости поверхности, в этом случае труба работает как гидравлически гладкая. По мере возрастания скорости толщина пристенного слоя уменьшается и выступы, ранее скрытые этим слоем, теперь начинают выдаваться из него и вызывают завихре­ния. Труба перестает быть гидравлически гладкой и начинает работать как шероховатая. *

Таким образом, одна и та же труба в зависимости от обстоя­тельств течения в одном случае может оказаться гидравлически гладкой, а в другом — гидравлически шероховатой.

Если труба заполнена неньютоновской жидкостью, то ее движе­ние начинается только после того, как касательные напряжения в пристенных слоях жидкости достигнут величины предельного напряжения сдвига. При этом вся масса жидкости начнет дви­гаться, скользя по прйстенным слоям, как твердое тело.

Такой вид течения назвали структурным, а’центральную часть потока, движущуюся с сохранением структуры, — ядром потока.

По мере увеличения приложенного давления (увеличения ско­рости течения) толщина пристенных слоев, в которых происходят взаимные сдвиги слоев потока, будет увеличиваться, а диаметр ядра соответственно уменьшаться. При этом скорость в слоях между стенкой, и ядром будет непрерывно изменяться от нуля до скорости ядра; можно представить, что при некотором значении скорости градиентные слои займут все сечение и структурный режим перейдет в ламинарный. Однако обычно во время умень­шения поперечных размеров ядра до некоторого предела плавное параллельное течение слоев нарушается, в силу чего этот режим правильнее называть квазиламинарным (Р. И. Шищенко, Б. Д. Ба­кланов).

По мере дальнейшего увеличения скоростей течения струк­турных жидкостей как в лотке, так и в трубах возникает турбу­лентность, характеризующаяся,’ как и в обычных жидкостях, пере­мешиванием струй потока и непрерывным изменением их скоро­стей как по величине, так и по направлению.

Влияние шероховатости на гидравлические сопротивления в трубах наиболее полно было изучено Никурадзе. Опыты прово-. дились в трубах, стенки которых оклеивались зернами песка’ различного размера, что и давало возможность, менять величину абсолютной шероховатости А, т. е. среднюю величину высоты вы­ступов (неровностей) стенок опытной трубы. Однако из сообра­жений подобия в расчетные формулы вводилась не абсолютная, а относительная шероховатость А, т. е. отношение абсолютной шероховатости к радиусу трубы( у некоторых авторов к диаметру трубы). Иногда абсолютную шероховатость обозначают буквой k, а относительную е. Таким образом, e = A = A/r=k/r. Величина, обратная е, называется относительной гладкостью е’. .

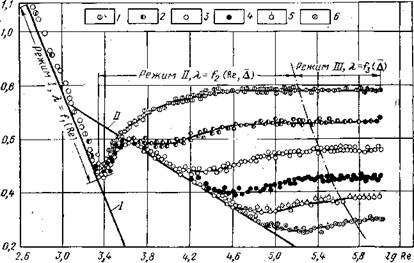
По данным проведенных опытов Никурадзе построил график зависимюстей Я = /(Re, А), на котором четко выделяются три само­стоятельные зоны: первая — зона вязкого трения или ламинарного режима (прямая I на рис. 6), где значения Я зависят от Re и не зависят от шероховатости бтенок, т. е. A = fi(Re); вторая — пере­ходная зона турбулентного режима или зона смешанного трения, которая располагается между прямой II (гидравлически гладкие трубы) и пунктирной линией (вполне шероховатые трубы). В этой зоне в трубах с повышенной шероховатостью с самого начала воз­никновения турбулентности коэффициент Я зависит как от шеро­ховатости, так и от Re, т. е. Я=/2^е, А). Дальнейшее увеличение скорости потока приводит к тому, что Я приобретает постоянное значение, независимое от Re. Такое состояние потока, когда Я = = /з(А), характерно для третьей зоны, которую называют зоной вполне шероховатых труб, автомодельной зоной, областью квад­ратичного трения и т. п. .

Во второй зоне при небольшой шероховатости значения Я могут располагаться непосредственно на прямой II и в этом случае зависят только от Re, т. е. Я=Д4(Re). Тем самым прямая II может рассматриваться как. четвертая самостоятельная зона. Но если при этой же шероховатости скорость потока увеличивать, то тол­щина пристенного слоя б может уменьшиться настолько, что — выступы шероховатости начнут обтекаться турбулентным ядром и тогда труба станет гидравлически шероховатой. В этом случае

снова Я = /2 (Re, Д). Таким образом, одни и те же трубы в зави­симости от величины Re могут быть «гидравлически гладкими», «шероховатыми» и «вполне шероховатыми».

Примерные границы отдельных зон определяются следующими соотношениями: первая зона Re^2320j вторая зона 400^Re^ s£80e’; третья зона 80e'<Re< 1000е’; четвертая зона Re>

> 1000 в’.

IgWOJL Рис. 6. Зависимость lglOOA, от lgRe, по опытам Никурадзе: I _ ?.=64/Re; II — Я=£,3164/Re 0,25j_ III — A,=const-f(K). 1 -^Д-0,0666; 2 — Д=0,0327; 3 — Д-0,0166; 4 — Д=0,008; 5 — Д=0,004; 6 — Д=0,002

Исследования Никурадзе были подтверждены в работах многих зарубежных и советских ученых. Тем не менее, как показали иссле­дования, выполненные в Советском Союзе И. А. Исаевым, Г. А. Му — риным, Ф. А. Шевелевым и в Англии — Кольбруком, они не могут быть механически перенесены на обычные стальные трубы. Учесть же неравномерность и неоднородность естественной шероховатости непосредственными измерениями невозможно. Поэтому наряду с понятием абсолютной шероховатости стало употребляться понятие эквивалентной или гидравлической шероховатости k9. Она нахо­дится в результате гидравлического испытания и представляет собой такую высоту выступов условной (абсолютной) шерохова­тости, при которой создается сопротивление, равное действитель­ному сопротивлению испытываемой трубы. Величина эквивалент­ной шероховатости может быть найдена из формулы Никурадзе —

Прандтля для вполне шероховатых труб (VI.27) с заменой в ней величины k на kg, т. е.

1 d 3,7d

-^=- = 21g — + l,14 = 21g-^- . (III.23)

В литературе известны еще и другие характеристики шерохова­тостей k и k2, которые связаны между собой и величиной kg следующим соотношением [I]:

kg к 10*! » 0.7^2- (Ш.’54)

Что касается влияния шероховатости на характер течения

вязко-пластичных жидкостей, то этот вопрос пока еще изучен

крайне недостаточно для всех режимов движения.

Комментарии запрещены.