Бурение грунтовых зондов, установка энергетических колодцев

Теплоотдача относится к категории сложных процессов, про­текание которых зависит от многих факторов. Так, кроме перепада температур между средой и стенкой At на теплоотдачу существен­ное влияние оказывают форма стенки, ее геометрические размеры,’ состояние поверхности (шероховатость). Не менее важное влияние на характер — теплоотдачи оказывают физико-механические и тепло­физические свойства движущейся среды (теплоносителя), такие как коэффициент теплопроводности Я, удельная теплоемкость с, плотность р, кинематическая или динамическая вязкость, коэф­фициент температуропроводности а и др. ,

Исследования показали, что характер конвективного теплооб­мена в значительной мере зависит от режима движения. Так, при ламинарном режиме перенос тепла крайне незначителен и можно считать, что весь теплообмен внутри потока обусловливается теп­лопроводностью жидкой среды. При турбулентном режиме, отли­чающемся бурным движением потока, возникающие в нем вихри создают благоприятные условия для проникновения отдельных масс от ядра потока к стенкам и переноса некоторого количества тепла. А так как теплопроводность жидкостей сравнительно неве­лика, то основной причиной теплообмена при турбулентном ре­жиме является интенсивность переноса количества движения. Однако и в первом и во втором случае у самой стенки образуется пограничный подслой толщиной б, который, будучи неподвижным, может проводить тепло исключительно за счет теплопроводности.

Если движение теплоносителя обусловлено действием внешних сил (например, насос), то говорят о вынужденной конвекции. Если же движение происходит за счет разности плотностей нагретых и холодных частиц жидкости, то такую конвекцию называют есте­ственной. ,

Конкретизируя задачу, предположим, что промывочная жид­кость, имеющая среднюю температуру, прокачивается через бурильные трубы, причем наружная поверхность этой трубы по всей ее длине омывается жидкостью, имеющей постоянную темпе­ратуру *ж, <*Ж1.

Наружный диаметр бурильных труб по всей длине колонны (без учета замков) равен d2, а внутренний d. Стенки труб пред-

полагаются однородными, имеющими коэффициент теплопровод­ности Я.

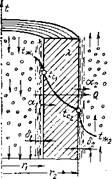
Температуру стенок трубы для внешней поверхности стенки обозначим (с> и для внутренней tCl (рис. 11). Примем далее, что со стороны горячей жидкости коэффициент теплоотдачи равен аь а со стороны холодной а2-

Рис. 11. Схема процесса теплоотдачи при движе­нии жидкости в трубе (горячая) и за трубой (холодная)

Будем рассматривать некоторый отрезок бурильной колонны длиной I, на протяжении которого можно считать, что все пере­численные параметры ((ж, tc, а и т. д.) не изменяют своей величины. При установив­шемся тепловом состоянии системы количе­ство тепла, отданное горячей и принятое холодной жидкостями, должно быть одним и тем же; тогда на основе изложенного вы­ше можно написать:

а) для потока тепла, идущего от горячей жидкости к внутренней стенке трубы,

Q

— = 4i = «lJtdi (<Ж1 — *Cl);

б) для потока тепла, идущего от внут­

Поскольку в выражение (III.56) входит qi, то в данном случае величина будет относиться к 1 м трубы.

Введение коэффидентов ki и rt позволяет записать выражение для q в виде

qi = — JZi ^ = (*«.-*«,)■ (III. 59)

ri

В случае теплопередачи через многослойную цилиндрическую стенку выражения для и кг примут вид

П = —l— + J) [(м-°С)/Вт]; (111.60)

TOC o "1-5" h z ai“i 2%i df

k[ = ————————————————————- — [Вт/(м-°С)1 (Ш.61)

1 . — Л 1 . di+1 ~ 1

+ £ 91. ln

ai^i i= i di a2^(n+i)

С целью использования рассмотренных закономерностей для решения ранее поставленной задачи о теплопередаче в условиях реальной скважины обратимся к рис. 5. Согласно обозначениям, принятым на этом рисунке для установившегося теплового со­стояния системы, когда количество тепла, отданного горячей и принятого холодной жидкостью, будет одним и тем же, можно составить следующие равенства:

а) для потока, тепла, идущего от породы к внешней стенке трубы I, ‘

Т =?* = г внутренней ее стенке,

q 2лА,„ (*п,— *i2)

In djdb

б) для потока тепла, идущего от внешней стенки трубы / к

Q 2^i(*i2-‘i,)

— == а 1 =——————— 5

/ 41 lnds/d*

в) для потока тепла, идущего от внутренней стенки трубы Г (или от внешней стенки трубы //) к внутренней стенке трубы II,

Q Ъг%п (*ц2 — #П1) ^

/ qi In djd3 ‘

г) для потока тепла, идущего от внутренней стенки трубы 1Г к восходящему потоку жидкости ж2,

Q

j —Й1 = ^/ji^—^2)’

д) для потока тепла, идущего от жидкости ж2 к наружной стенке трубы III,

Q

■ i — Я1 — ct2nd2 — *ш2)’

е) для потока тепла, идущего от наружной стенки трубы III к внутренней ее стенке,

q (^iii2—

~r = qi=1 in drfdi : ‘

ж) для потока тепла, идущего от внутренней стенки трубы III

К ЖИДКОСТИ Ж,

Составленные равенства позволяют определить частные тем­пературные перепады, складывая которые, можно найти полный температурный напор в рассматриваемой системе:

#iii —/ж! ~ л [ 2A, n ln db + Щ ln / + ML. 1пТ’ + ТГ + ГГ +

A ,_L, n А

TOC o "1-5" h z. г 01 , + .

“5 —1 dA z/tn з a3d3 a2d2

1 do 1 "1 at

’23Г ln~T + ~T = — ri> (ш-62)

/y4II dx 0Cjrfj J я ‘

тде rt — полное термическое сопротивление теплопередачи.

Отсюда в соответствии с (II 1.61) определим величину ki для рассматриваемого случая:

kt = — = —————————————— !—————— :——————— ;—-

4 2Х^1пСГ +_^_1пТ’ + Г_1п’Т+ ~1Г+ “T+“V+

2An d6 d4 Ац й3 a3d3 a2d2

1

1

(111.63)

h-*

2^III di

а выражение для пбтока тепла примет вид

(III.64)

Следует иметь в виду, что для тепловых процессов так же, как и для гидравлических, большое значение имеет длина началь­ного участка. При этом под начальным термическим участком понимается участок, на протяжении которого происходит тепловая стабилизация потока и, например, в условиях ламинарного режима с точностью до 1 % устанавливается предельное значение пара­метра Нуссельта, равное 3,65. Определить длину участка тепловой стабилизации можно из условия

—= 0,05; Ре = — , (111.65)

Ре а а

где Ре —среднее значение параметра Пекле, представляющего собой безразмерный комплекс; а — коэффициент температуропро­водности. ‘

Комментарии запрещены.