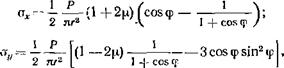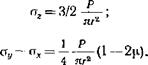Бурение грунтовых зондов, установка энергетических колодцев

Разрушению горной породы при внедрении в нее резца предшествует упругое напряженное состояние в породе. Распре­деление напряжений, возникающих в ней, изучают теоретически и экспериментально. Многие резцы, применяемые в породораз­рушающем инструменте, по своему действию с породой на за­бое до ее разрушения могут быть сведены к взаимодействию ци­линдра, сферы, круглого и длинного плоского штампа с плоско­стью, ограничивающей упругое полупространство. В связи с этим кратко рассмотрим некоторые результаты, полученные при решении контактных задач.

Задача Буссинеска. На рис. 1.8 изображена схема действия

сосредоточенной Р на упругое полупространство. В любой точке А напряженное состояние определяется следующими компонен­тами напряжений:

где г2=х2+г2. При ф = 0

Из последнего выражения следует, что на оси симметрии все напряжения являются сжимающими, что соответствует все­стороннему сжатию. На поверхности образца, т. е. при ф=зх/2,

сгг = 0;

Равенство оу= —Ох указывает, что на поверхности полупро­странства имеет место чистый сдвиг.

При г->-0 агг*-о°. Следовательно, сжимающие напряжения на поверхности из вышеприведенных формул определить нельзя.

Действительно, при 2 = 0 а2 = Р’-, при 2->-оо аг-э-0.

Согласно принципу Сен-Венана, сосредоточенную силу Р можно заменить эквивалентной ей по действию распределен­ной нагрузкой Р’ по кругу радиуса а. В этом случае нормаль­ные напряжения определяются на любом расстоянии от по­верхности следующей формулой:

Упругая деформация на поверхности круга в этом случае распределена неравномерно. В центре круга

2 (1 — ц2) Р’а Е

Влас­

на контуре

1Ро. в-

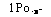1,27(1 — ца) Р’а

Рис. 1.8. Дсіістшю сосредото­ченной нагрузки Р на упругое ПОЛ у п ростр а і їство

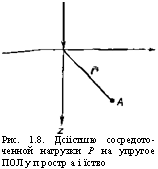Буссинеск рассмотрел задачу, когда перемещения под круг­лым жестким штампом диаметром 2 а во всех точках контакта

Рис. 1.9. Деформация хрупкой горной породы при вдавливании плоского круглого штампа:

1 — распределение давления под штампом; 2 — распределение максимальных касатель­ных напряжений (по изохроме). Разрушение горной породы при достижении конечной упругой деформации показано конусом сЬс

одинаковы. В этом случае давление под штампом распределя­ется неравномерно и определяется следующей формулой:

Р ———— Л ^ (1.8)

2па V(а2 — х2)

В центре штампа (л: = 0) давление

Р

на контуре (х=а), р-+оо.

При вдавливании штампа максимальные касательные на­пряжения тшах. имеющие одни и те же численные значения, рас­положены на окружностях (изохромах), проходящих через края штампа (рис. 1.9). Наибольшее из максимальных касательных напряжений находится на направлении оси штампа, на глубине
2 = 6=0,637. Численное значение ЭТОГО напряжения Хо, тах = = 0,33р, для коэффициента Пуассона р,=0,3. При 2=0, ттах= = 0,1 р.

Глубина Ь, на которой возникает то, шах. получила название критической, так как на этой глубине часто зарождается тре­щина, которая при увеличении нагрузки на штамп разраста­ется и, наконец, выходит па поверхность. Этот процесс обычно сопровождается круппым выколом породы. Диаметр образовав­шейся лунки, измеренной па поверхности вдавливания, намного больше диаметра штампа, что можно видеть на том же ри­сунке.

Решение задачи Буссинеска использовано Л. А. Шрейнером при разработке описанного выше метода определения твердо­сти породы. Основанием при разработке указанного метода по­служило следующее: разрушение породы начинается на кон­туре круглого штампа, что приводит к значительному выравни­ванию давлений под штампом. Поэтому для определения твер­дости породы можно применять штампы различных размеров.

При разработке метода определения твердости Л. А. Шрей — нер исследовал, влияиие величины площади штампа на числен­ное значение твердости породы. Эти исследования показали, что при увеличении диаметра штампа от 1,13 (5Ш=1 мм2) до 1,95 (5 т = 3 мм2) твердость уменьшается примерно на 5 %, а для штампа диаметром 3,58 мм (51П=10 мм2) на 10—12%- На основании этого был сделан вывод, что введение поправки на масштабный фактор при измерении твердости породы не­обязательно.

Задача Герца. Г. Герц рассмотрел взаимодействие двух кри­волинейных поверхностей. Когда взаимодействуют но образую­щим два цилиндра различных’радиусов /?1 и Р2, то в силу их упругого вдавливания соприкосновение происходит по пло­щадке шириной 2 а.

Г. Герц установил, что наибольшее давление возникает в центре площадки, так что распределение давления по ши­рине контакта

р(х)—^^Уа2—х2.

а

Из выражения

+°

Р = 5 р(х)йх,

—а

определяется величина

2Р

Ртах >

па

где Р — нагрузка, отнесенная к единице длины контакта.

Н. М. Беляев нашел, что то, шах находится в точке Ь, лежа­щей на нормали, восставленной в середине полоски контакта. Численное значение То, тах = 0,304 Рта*.

Для бурения может иметь интерес случай, когда /?2->-оо. Это означает, что происходит контакт образующей цилиндра радиуса с плоскостью (с забоем). В этом случае

Г 4РЯ	(1 — ^
п	Е
	ЕР

в=у

V яЯ (1 — ц2)

где относится к лезвию резца, Е и р,— к породе.

Когда с полупространством взаимодействует шар радиуса /?], удельное давление иа контакте шара с плоскостью (Я2-^-ао) распределено так, что его численные значения пропорциональны ординатам полушара, диаметральным сечением которого явля­ется круг контакта. Распределение давления определяется сле­дующей формулой:

р(г)= Ргпа— У а2—гг, а

а — радиус круга контакта; г — расстояние от центра площади контакта.

Максимальное давление будет при г=0:

3Р

Ртах ~ 2яа* ‘

В этой точке материал (порода) находится в условиях все­стороннего сжатия.

Наибольшее главное касательное напряжение, как устано­вил А. П. Динник, возникает в точке на линии центров при Ь = 0,47 а: *

То, шах —■ 0,31 ртах-

Наибольшее растягивающее напряжение находится на окружности круга контакта

^гшах 0,133Ртах.

Для /?2—>-оо величина

а^_ ,У ЗРК (1-и«Г

и

__1_ 13/Г 6 Р £2

РтаХ 71 V Я (1 — |12)

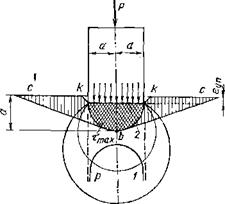
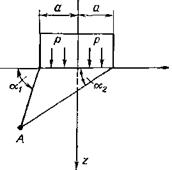
Задача о внедрении штампа большой длины (М. Садовский, Л. Надан и др.). На длинную полоску шириной 2а действует

распределенное давление с интенсивностью р (рис. 1.10). На­пряжения в точке А:

Оу= — — |аа —аг + у (sin 2а2—sin 2ах)|.

—

а,=

(а2 —аг—-(sin2a2—sin 2^)1. эх ^ 2 )

SHAPE \* MERGEFORMAT

-X

Рис. 1.10. График определения на­пряжений в породе при вдавлива­нии в нее длинного плоского штампа шириной 2а

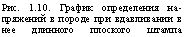В пределах поверхности дав­ления, когда czi — зх и а.2 = 0, ау = = р и аг= —р.

На оси г, после введения угла (ai = aia2 = n—a; a2—ai = я—2ai sin 2ct! = sin 2 a; sin 2a2= =—sin 2a) формулы принимают следующий вид:

о у = —p/я (я—2a—sin 2а),

аг — — p/я (я—2а sin 2а).

Касательные напряжения равны

о х — ог

—

т =

sin 2a.

л

При 2=0 и «=0 г=0. При a = 45°

То,

р/я.

і і

Из этого следует, что максимальные касательные напряже­ния возникают на глубине Ь = а.

Таблица 1.2 — Форма нпдентора Положение критической точки b на глубине Численное значение Т0. Ш0Х Круглый плоский штамп с радиусом а 0,637а 0,33 р (р — среднее) Сфера с радиусом контакта а 0,47а 0,31ртах Цилиндр такта 2а с шириной полоски кон- 0,78а 2Р/ла (Р — нагрузка на единицу длины (по­лоски) Длинная полоска шириной 2а а р/л (р — равномерно распределенное дав­ление на поверхности)

Сводные данные о местоположении критической точки b и численного значения т0> max для рассмотренных задач сведены в табл. 1.2.

Теоретическими исследованиями установлено, что если пло­ский штамп перемещается и на контакте его с поверхностью возникает значительная сила трения, то критическая точка Ъ смещается в направлении перемещения штампа и расположена ближе к поверхности контакта.

Деформация разрушения горных пород

Наиболее трудоемкими для бурения являются крепкие гор­ные породы. При бурении их решающее значение имеет осевая нагрузка на забой. В зависимости от того, с каким усилием воздействует резец на породу, характер разрушения ее может быть различным. Это оказывает влияние iia скорость углубки, расход долот и коронок.

Различают три следующих вида деформации разрушения, отличающихся по характеру п эффективности.

1. При небольшой осевой нагрузке на резец, когда давление на контакте резца с породой

РкСРш- ‘ 0.9)

Резец не может разрушать породу так, чтобы преодолеть ее структурную прочность — твердость породы. При перемещении резец производит истирание породы на забое. Разрушение по­роды происходит за счет работы сил трения па контакте лезвия с породой. Частицы отделившейся породы очень малы. Ско­рость бурения небольшая. Углубление скважины проходит мед­ленно. Такой вид деформации разрушения получил название поверхностного истирания породы.

Если увеличить осевую нагрузку на резец настолько, чтобы под действием ее происходили нарушения межкристаллических связей в породе, развивались бы дефекты ее структуры и, осо­бенно, трещины усталости под влиянием многократного при­ложения нагрузки в одной и той же точке забоя, то при пере­сечении многочисленных трещин происходит отделение более крупных частиц породы, бурение идет эффективнее, хотя дав­ление па контакте резца с породой все еще остается меньше твердости, что можно записать так:

Рк<Рш. (110)

Этот вид деформации получил название усталостного раз­рушения.

Дальнейшим увеличением нагрузки па резец добиваются активного внедрения лезвия резца в породу. В результате этого резец, перемещающийся на забое, непрерывно преодолевает

структурную прочность поролы, срезая породную стружку. Дав­ление на контакте с породой

Рк>Р,

Такой вид деформации называется объемным разрушением. При ■ объемном разрушении на забое скважины отделяются зна­чительные объемы породы, разрушение ее происходит эффек­тивно.

Объемному разрушению предшествует формирование под резцом пространственного или объемного напряженного со­стояния, близкого к всестороннему сжатию, при разрядке ко-

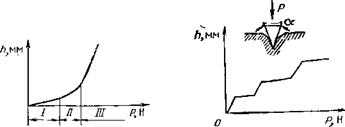
Рис. 1.11. График, характеризующий глубину внедрения острого резца в по — 4 роду при различных видах деформации разрушения: / — область поверхностного разрушения; II — область усталостного разрушения; III— область объемного разрушения

Рис. 1.12. График зависимости глубины внедрения конуса в стекло от на­грузки

торого основная роль принадлежит касательным напряжениям и напряжениям отрыва.

График, изображенный на рис. 1.11, качественно характе­ризует глубину внедрения резца в породу и, следовательно, величину механической скорости бурения при истираним /, усталостном II и объемном III разрушениях породы в зависи­мости от осевой нагрузки на резец с0.

При объемном разрушении хрупкой породы единичным рез­цом наблюдается скачкообразность разрушения породы. Так, при некотором значении осевой нагрузки удельное давление на контакте лезвия резца с породой достигает значения твердости рш. В этом случае происходит отделение первого, сравнительно небольшого объема породы. Чтобы резец продолжал внед­ряться в породу, необходимо дальше повышать осевую на­грузку. При этом площадь контакта лезвия с породой, вслед­ствие его клиновой формы, будет возрастать и размеры напря­женной зоны увеличатся. При некотором новом значении нагрузки па резец и достижении предельного напряженного со­стояния в большем по объему пространстве’ произойдет отделе­ние второго, более крупного объема породы. До момента опре­
деления этого объема удельное контактное давление под рез­цом рк>рш, так как на величину давления может оказывать влияние размер зоны напряженного состояния под резцом или глубина внедрения резца. После отделения второго объема кон­тактов давление снова снизится до значения твердости рш. Если осевая нагрузка на резец будет повышаться и дальше, то может произойти отделение следующего, еще более крупного объема и т. д. На рис. 1.12 показана Зависимость глубины внедрения конуса в стекло от нагрузки. Участки ступенчатой кривой, имеющие большие углы наклона к оси ординат, соответствуют

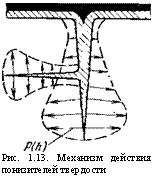
Рис. 1.13. Механизм дейст­вия понизителей твердости

относительно свободному погружению конуса. Пологонаклонные участки ло­маной линии соответствуют упругому сжатию стекла с одновременным от­делением его небольших частиц.

Увеличение объемов отделяемой породы при повышении площади пят­на контакта резца с породой пред­ставляет определенный интерес при разработке теории бурения, так как при таком механизме разрушения горной породы проходка иа коронку должна зависеть не только от глуби­ны внедрения резца, но и от объема породы, выбуриваемой резцом.

Понижение механической прочности горных пород в про­цессе разрушения. Исследования показали, что при бурении внешняя среда, в частности вода, активно участвует в разру­шении горных пород, особенно если она содержит в себе адсор­бирующие вещества, получившие название понизителей твердо — ‘сти, а сам метод — адсорбционным понижением твердости (эф­фект П. А. Ребиндера).

Механизм понижения твердости состоит в следующем. При разрушении породы на забое происходит как отделение частиц породы, так и образование зоны предразрушения, богатой мик­ротрещинами и микрощелями (рис. 1.13). В зоне предразруше­ния твердость породы в той или иной степени понижена. Обра­зование зоны предразрушения свойственно хрупким породам. При разрушении породы адсорбционные слои проникают в мик­ротрещины и после снятия нагрузки не дают им сомкнуться, как бы расклинивают их. Прочность породы при этом понижа­ется на величину, большую, чем при обычных условиях разру­шения. Сказанное относится главным образом к твердым по­родам при разрушении их ударным, ударно-вращательным, алмазным вращательным способами с наложением на породо­разрушающий инструмент высокочастотных ударных импульсов.

Таким образом, действие понизителей твердости органиче­ски связано с самим процессом разрушения, т. е. понизители

твердости не могут изменить прочности пород без процесса раз­рушения.

В качестве понизителей твердости могут применяться раз­личные поверхностно-активные вещества (ПАВ). Кроме того, понизителями твердости кварцсодержащих пород могут быть хлористый натрий, хлористый аммоний,.сода, известь; в карбо­натных и сульфатных породах — едкий натрий, известь.

При алмазном бурении может представлять интерес приме­нение поверхностно-активных веществ для борьбы с зашлифо — ванием матрицы коронки и алмазов при бурении кварцсодер­жащих пород.

Влияние масштабного фактора на сопротивление породы разрушению

р, МПа Ш0 3000 2000 1000

0 0,1 0,2 0,3 0,Ь 0,5й. т

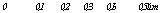Известно, что прочность твердого тела зависит от его раз­меров. При разрушении образца пород меньшего размера ве­роятность встретить дефекты структуры меньше. Поэтому прочность такого образца больше. На этом явлении осно­вано улучшение качества низко­сортных алмазов их дроблением.

Когда Л. А. Шрейнер изучал влияние размера напряженной зоны на сопротивление внедре­нию конуса в стекло, модели­рующее разрушение ХруПКОЙ ПО — рис. 1Л4 График зависимости со — роды, то ОН наблюдал, ЧТО При, противления стекла вдавливанию диаметре площади давления от размеров напряженной зоны меньше 0,5 мм сопротивление

вдавливанию зависит от размеров площади давления. Это явле­ние он объяснял проявлением масштабного фактора. На рис. 1.14 представлена опытная кривая, показывающая зависи­мость сопротивления вдавливанию конуса в стекло. По верти­кальной оси откладывается нагрузка, отнесенная к площади давления, по горизонтальной оси — диаметр площади истиниого контакта (пятна контакта).

Нагрузку, отнесенную к площади давления, Л. А. Шрейнер называет мерой сопротивления вдавливанию. Из рисунка видно, ‘ что только при диаметре площади <2> 0,5 мм сопротивление вдавливанию практически остается постоянным. Влияние мас­штабного фактора может вызывать снижение скорости про­ходки при бурении с невысокими осевыми нагрузками на забой ‘ или же при бурении коронками, армированными очень мелкими резцами, например алмазами, за счет повышенного сопротивле­ния породы внедрению резцов. Оно также должно проявляться в относительном снижении сопротивления внедрению резца, имеющего небольшое предварительное затупление лезвия.

Напротив, при большом предварительном затуплении со­противление породы внедрению резца возрастает за счет, повы­шенных затрат энергии на более Мелкое дроблеиие породы под площадью затупления. Это уменьшает глубину внедрения резца при заданном осевом усилии на резец.

Энергоемкость разрушения горных пород при бурении

Наиболее общим показателем, определяющим энергоемкость разрушения породы при бурении, является удельная работа разрушения

= 0.12)

где V — объем разрушенной породы; Ап — работа, затраченная на разрушение породы.

Когда разрушение породы производится вдавливанием в нее плоского штампа с круглым основанием, то работа, затрачивае­мая на упругую деформацию,

Ауп

Ре уп

где Р — нагрузка па штамп; еуп — упругая деформация, соот­ветствующая этой нагрузке. Величина

Р(1-Р-2)

‘ 2 аЕ

где а=йш/2. Поэтому

, ^Р*(1-Ц2)

•’Чуп —

4 аЕ

Полная работа разрушения

4 аЕ

Отношение полной работы к площади штампа, при гш = а

^ л, = р,(1->-12) к,

па2 4 аЕна?

к — коэффициент пластичности.

Умножив числитель и знаменатель этого выражения на я а, получим удельную контактную работу А8, выраженную в зави­симости от твердости породы:

Приняв глубину лунки Н=а, а угол при вершине конусооб­разной лунки 120°, приближенно определяем объем разрушен­ной породы У^да3. Тогда объемная удельная работа разру­шения

А

4 аЕпФ

Для перехода от нагрузки к твердости умножим числитель и знаменатель этого выражения на л, тогда получим

р*,(.-„*) £«(1-|.») 3) у (ля2)2 4£ 4£

Экспериментально удельную объемную работу разрушения породы определяют путем измерения площади диаграммы (Р — еу), и по ней находят полную работу разрушения Аа, после чего определяют объем лунки. С этой целью осторожно очищают лунку от разрушенной породы и заполняют ее пара­фином. Определив массу парафина на весах, делением ее на плотность находят объем лунки. После этого определяют

Ау — А„/У.

Определение удельной работы разрушения динамическим способом

Н. И. Любимов, Ю. А. Пешалов и А. П. Угаров разработали прибор ПОУВ-1 и методику определения удельной объемной ра­боты разрушения породы на образцах неправильной формы, назвав эту величину ударной вязкостью. Метод заключается в следующем. Для опытов отбираются 3—5 кусочков породы компактной формы, объемом по 8—12 см3, наибольшее сечение которых не должно отличаться от наименьшего более чем вдвое. Величину ударной вязкости определяют па копре с ударником массой 2 кг при высоте падения 25 см. Образец породы поме­щают в металлический стакан и ударяют по нему, пока он не расколется на две-три части. Это необходимо для определения усталостных свойств породы. Затем раздробленный материал высыпается в сито с отверстием 7 мм и отсеивается. Отсеяв­шийся на сите материал помещают в стакан и наносят по нему еще от двух до пяти ударов, а затем снова отсеивают. Эти опыты повторяются до полного раздробления породы, до фрак­ции меньше 7 мм. При проведении опытов необходимо следить, чтобы не производилось переизмельчение фракции меньше 7 ММ. Поэтому число ударов по разрушенному образцу для твердых пород обычно не должно превышать пяти. При дроблении более слабых пород ограничиваются вместо пяти двумя, тремя уда­рами.

Мерой затрат энергии на разрушение служит число ударов, а удельная работа разрушения определяется по формуле

Ау’.у(1.14)

где Ау, у — удельная ударная вязкость, Дж/м2; Р — масса удар — , ника, равная 2 кг; Л— высота сбрасывания груза, равная

0, 25 м; п — полное число ударов; — плотность горной по­роды, г/см3; (? — масса раздробленной породы (фракции 7 мм), г. Из данных, полученных последовательным дроблением

3— 5 образцов, определяется среднее значение величины Ау, у.

Рассмотренный метод определения удельной работы разру­шения учитывает влияние удара на разрушение, а также скры­тых дефектов и трещиноватости пород на их динамическую прочность. Величину Ау, у Н. И. Любимов использовал при анализе данных скорости бурения гидро — и пневмоударниками: Он считает, что начальная скорость бурения, когда износ буро­вой коронки еще невелик, существенно зависит от этой харак­теристики.

Комментарии запрещены.